
- •Частина II Диференціальне числення функцій багатьох змінних Розділ 1. Поняття дійсної функції багатьох змінних
- •Розділ 2. Диференційовність функцій багатьох змінних § 1. Поняття диференційовної функції. Часткові похідні. Необхідні умови диференційовності
- •§ 2. Достатні умови диференційовності функції багатьох змінних
- •§ 3. Диференційовність складної функції.
- •§ 4. Інваріантність форми диференціала функції багатьох змінних.
- •§ 5. Похідна за напрямком. Градієнт.
- •Розділ 3. Частинні похідні і диференціали вищих порядків § 1. Частинні похідні вищих порядків
- •§ 2. Достатні умови незалежності змішаних частинних похідних від порядку диференціювання.
- •§ 3. Диференціали вищих порядків
- •§ 4. Формула Тейлора для функцій багатьох змінних
- •Розділ 4. Неявні функції § 1. Існування неявної функції однієї змінної
- •§ 2. Існування неявної функції багатьох змінних
- •§ 3. Існування неявної функції, яка задається системою рівнянь
- •Розділ 5. Екстремуми функцій § 1. Поняття екстремума функцій багатьох змінних
- •§ 2. Деякі відомості з теорії квадратичних форм
- •§ 3. Достатні умови існування екстремуму
- •§ 4. Умовний екстремум
- •Частина III. Розробка електронного посібника “Елементи функціонального аналізу та диференціальне числення функцій багатьох змінних”
- •Програмне середовище підручника
- •Як працювати з підручником?
§ 2. Достатні умови диференційовності функції багатьох змінних
В попередньому параграфі ми показали, що, якщо функція диференційовна в точці, то в даній точці існують часткові похідні. Обернене твердження взагалі кажучи не вірне. Але при цьому має місце наступна теорема.
Теорема 2.1. Нехай функція U=(x1; x2;…;xn) в деякому околі точки А(х1(0); x2(0);…;xn(0)) має всі частинні похідні. Якщо вони є функціями неперервними в точці А, то дана функція – диференційовна в цій точці.
Доведення. Для простоти викладу будемо вважати, що наша функція залежить від двох змінних, U=f(x; y), A(x0; y0).
Надамо
х0,
у0
прирости
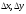 такі, що точка
такі, що точка
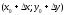 належить
околу, в якому існують часткові похідні.
Використовуючи теорему Лагранжа,
одержимо:
належить
околу, в якому існують часткові похідні.
Використовуючи теорему Лагранжа,
одержимо:
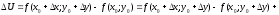
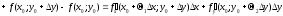 ,
де
,
де
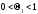 ,
,
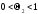 .
Оскільки за умовою f
/x
і f
/y
– неперервна
в точці х0,
у0,
то величини
.
Оскільки за умовою f
/x
і f
/y
– неперервна
в точці х0,
у0,
то величини
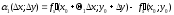 і
і
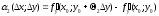 прямують до
нуля, коли
прямують до
нуля, коли
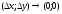 .
Знайшовши з останніх двох рівностей
перші доданки справа і підставивши їх
у суму, одержимо:
.
Знайшовши з останніх двох рівностей
перші доданки справа і підставивши їх
у суму, одержимо:
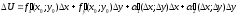 ,
а це означає,
що наша функція в точці А
є диференційовною.
Теорему
доведено.
,
а це означає,
що наша функція в точці А
є диференційовною.
Теорему
доведено.
§ 3. Диференційовність складної функції.
Коли
ми розглядали поняття диференційовності
функції, то в представленні
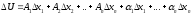 вважалося,
що
вважалося,
що
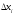 одночасно
не можуть дорівнювати нулю. Тобто функції
і
не визначені в точці (0,...,0). Якщо доозначимо
і
в точці (0,0,...,0), поклавши і(0,...,0)=0,
то рівність (1.1) матиме зміст і тоді, коли
всі
одночасно
не можуть дорівнювати нулю. Тобто функції
і
не визначені в точці (0,...,0). Якщо доозначимо
і
в точці (0,0,...,0), поклавши і(0,...,0)=0,
то рівність (1.1) матиме зміст і тоді, коли
всі
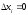 .
.
Нехай функції
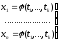 (3.1)
(3.1)
визначені в області D1Rk, а функція U=f(x1,…,xn) визначена в області DRn при чому, якщо точка (t1,…,tk)D1, то точка (1(t1,…,tk ),…, n(t1,…, tk))D. Тоді ми одержимо складну функцію U=f(1(t1,…,tk ),…, n(t1,…, tk)), яка визначена в області D1.
Теорема
3.2. Нехай
всі функції (3.1.) диференційовні в
А(t1(0),…,tk(0)),
а функція
U=f(x1,…,xn)
диференційовна
в точці В(x1(0),…,xn(0)),
де
хі(0)=I(t1(0),…,tk(0)),
тоді складна функція U(t1,…,tk)
–диференційовна в точці А
і при цьому її часткові похідні
обчислюються по формулі:
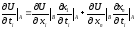 ,
деі=1,...,k.
,
деі=1,...,k.
Доведення. Для простоти викладок, проведемо доведення, коли U=f(x1,x2), x1=1(t1, t2, t3); x2=2(t1, t2, t3), A=(t1(0), t2(0), t3(0)), B=(x1(0), x2(0)).
Оскільки функції 1, 2 диференційовні в точці А за умовою, то надавши t1(0), t2(0), t3(0) прирости t1, t2, t3, які одночасно всі не дорівнюють нулю, прирости функцій х1, х2, що відповідають цим приростам, можна записати у вигляді:
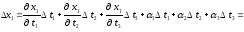
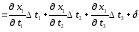 (3.2)
(3.2)
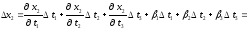
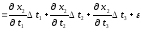 ,
(3.3),
,
(3.3),
де
і,
і0,
а значить
і
0,
коли
tk0.
Оскільки
х1(0),
х2(0),
одержали
прирости х1,
х2,
які обчислюються
за допомогою формул (3.2), (3.3), то в силу
того, що
U=f(x1,
x2)
в
точці
В
диференційовна, її приріст в цій точці
можна записати у вигляді:

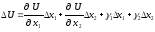 (3.4),
(3.4),
тут 1, 20, коли (х1,х2)(0,0) (при цьому можуть х1=х2=0).
Підставивши (3.2) і (3.3) в (3.4), одержимо:
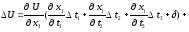
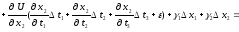
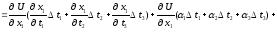
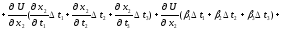
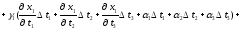
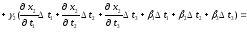
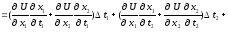
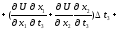
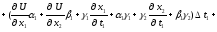
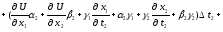
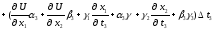
Замінивши множники біля t1, t2, t3 , в останніх трьох доданках, відповідно на 1, 2, 3, отримаємо:
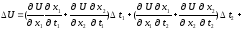
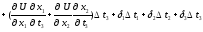
Якщо
t1,
t2,
t30,
то 1,
2,
30,
1,
2,
30,
і х1,
х20,
а значить 10,
20.
Тому 1,
2,
30.
Звідси робимо
висновок, що функція U(t1,
t2,
t3)
– диференційовна в точці
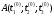 ,
і при цьому
,
і при цьому
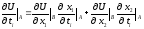 ,
деі=1,
2, 3.
,
деі=1,
2, 3.
