
- •Міністерство освіти і науки україни
- •Розділ і електронні підручники як засіб підтримки учбового процесу
- •Розділ іі технологія створення електронного підручника
- •1. Інструментальне забезпечення. Редактор FrontPage
- •1.1 Вставка тексту
- •1.2 Використання спеціальної вставки
- •1.3 Виділення тексту
- •1.4 Копіювання
- •1.5 Видалення тексту
- •1.6 Розриви тексту
- •1.7 Шаблони
- •1.8 Шаблони сайтів
- •1.9 Шаблони сторінок
- •1.10 Створення фреймів
- •1.11 Шрифти
- •1.12 Символи
- •1.13 Форматування абзаців
- •1.14 Списки
- •1.15 Створення гіперпосилань
- •1.16 Графічні формати
- •1.17 Збереження зображень
- •1.18 Колекція ілюстрацій
- •2 Характеристика та етапи створення електронного підручника
- •Розділ ііі ряди Числові ряди.
- •1.2 Знакододатні ряди. Умови збіжності таких рядів.
- •1.3 Абсолютно та умовно збіжні ряди
- •1.4 Ознаки збіжності знакозмінних рядів.
- •1.5 Множення рядів
- •Функціональні послідовності та ряди
- •2.1 Збіжність, рівномірна збіжність функціональних рядів і послідовностей
- •2.2 Властивості рівномірно збіжних послідовностей і рядів
- •Степеневі ряди
- •3.1 Область збіжності степеневого ряду. Властивості сум степеневих рядів
- •3.2 Розклад функції у степеневий ряд. Біноміальний ряд
- •Висновок
- •Список використаної літератури
Степеневі ряди
3.1 Область збіжності степеневого ряду. Властивості сум степеневих рядів
Означення. Ряд виду
![]() ,
(1)
,
(1)
де
![]() ,
,![]() ,
,![]() ,…
,…![]() ,…
– деякі дійсні числа, називається
степеневим рядом. Числа
,…
– деякі дійсні числа, називається
степеневим рядом. Числа![]() ,
,![]() ,…
,…![]() ,…
називаються коефіцієнтами цього ряду
(які незалежні від числа
,…
називаються коефіцієнтами цього ряду
(які незалежні від числа![]() ).
).
Як і для будь-якого функціонального ряду, так і для степеневого, першою проблемою при роботі з ним є встановлення області збіжності. Відповідь на цю проблему дають наступні роздуми. Утворимо ряд з модулів
![]() (2)
(2)
і застосуємо до нього радикальну ознаку Коші. Отримаємо
![]() ,
де
,
де
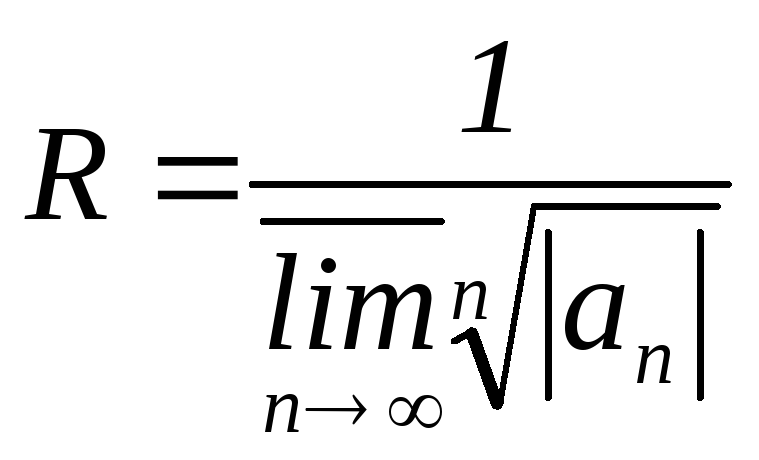 ,
якщо знаменник дорівнює нулю, то
,
якщо знаменник дорівнює нулю, то![]() і
і![]() ,
коли знаменник
,
коли знаменник![]() .
.
якщо
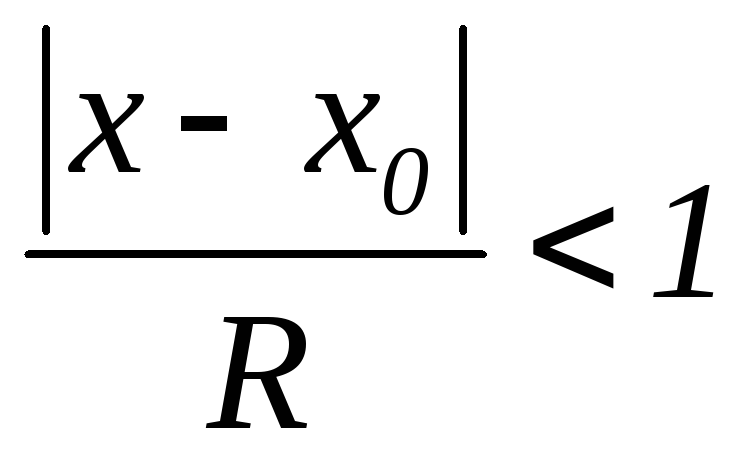 ,
то
,
то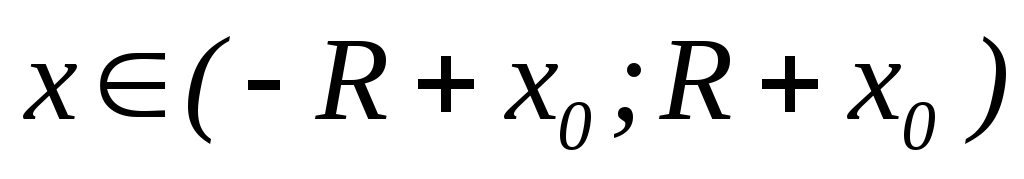 і ряд (2), а отже, і (1) – збіжний на інтервалі
і ряд (2), а отже, і (1) – збіжний на інтервалі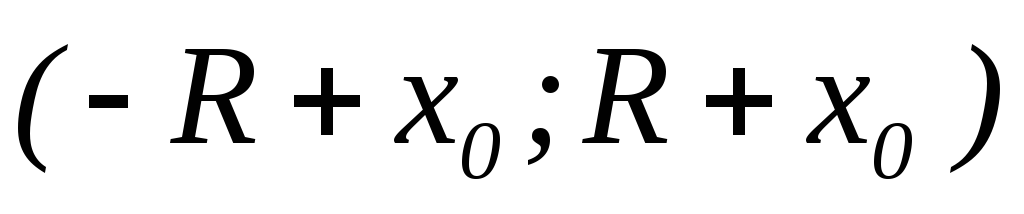 ,
причому абсолютно;
,
причому абсолютно;якщо
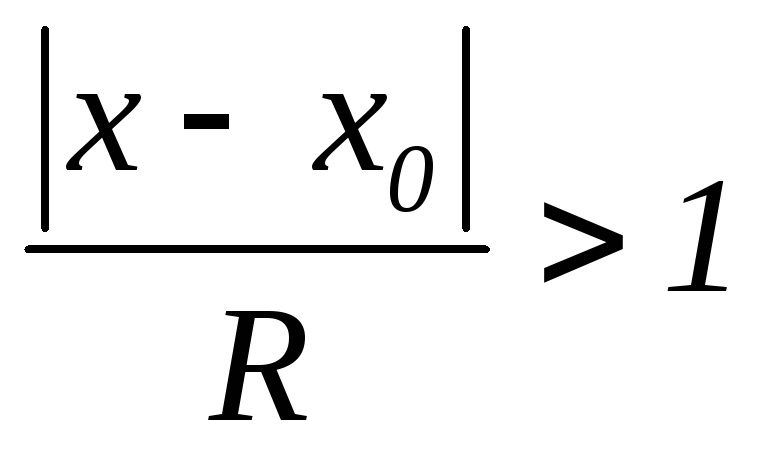 ,
то ряд (2) – розбіжний на
,
то ряд (2) – розбіжний на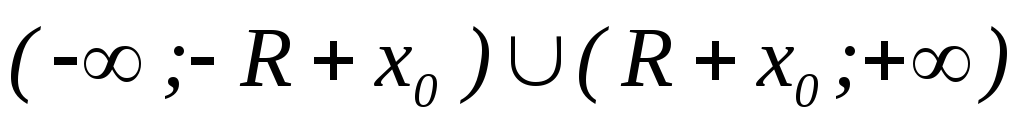 ,
тобто, ззовні
,
тобто, ззовні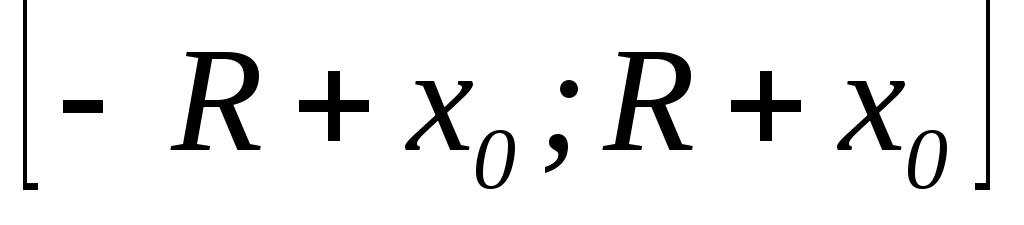 ,
а значить розбіжним буде і ряд (1)
(подумайте чому?);
,
а значить розбіжним буде і ряд (1)
(подумайте чому?);якщо
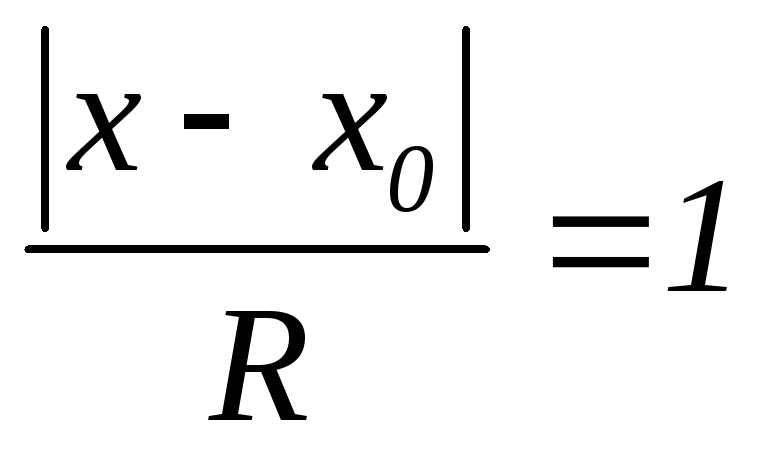 ,
то невідомо якими будуть ряди (1) і (2) –
збіжні чи розбіжні.
,
то невідомо якими будуть ряди (1) і (2) –
збіжні чи розбіжні.
Підсумовуючи все одержане вище, ми помічаємо, що довели наступне твердження.
Теорема1.
(Коші-Адамара про інтервал збіжності
степеневого ряду). Якщо
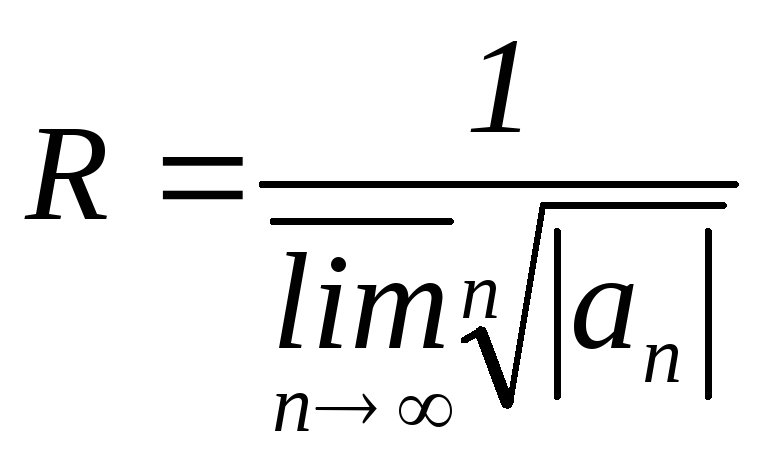 ,
то степеневий ряд (1) абсолютно збіжний
на інтервалі
,
то степеневий ряд (1) абсолютно збіжний
на інтервалі![]() ,
(коли
,
(коли![]() ,
то цей інтервал перетворюється на всю
числову вісь, коли
,
то цей інтервал перетворюється на всю
числову вісь, коли![]() ,
то він зводиться до точки
,
то він зводиться до точки![]() )
і розбіжний зовні відрізка
)
і розбіжний зовні відрізка![]() .
.
Домовимось
далі називати одержане вище число![]() радіусом збіжності степеневого ряду,
а інтервал
радіусом збіжності степеневого ряду,
а інтервал![]() – інтервалом збіжності степеневого
ряду. Отже, ця теорема майже повністю
відповідає на питання про область
збіжності степеневого ряду (1).
– інтервалом збіжності степеневого
ряду. Отже, ця теорема майже повністю
відповідає на питання про область
збіжності степеневого ряду (1).
З’ясуємо далі, чи є цей ряд рівномірно збіжним.
Теорема2.
(Про рівномірну збіжність степеневого
ряду). Степеневий ряд (1) з відмінним від
нуля радіусом збіжності є рівномірно
збіжним на будь-якому відрізку
![]() ,
який належить інтервалу збіжності.
,
який належить інтервалу збіжності.
▲
Позначимо
через
![]() ,
тоді, оскільки, відрізок
,
тоді, оскільки, відрізок![]() належить інтервалу збіжності, то точка
належить інтервалу збіжності, то точка![]() належить інтервалу
належить інтервалу![]() .
Отже, в цій точці ряд (1) є абсолютно
збіжним, тобто збіжним є ряд
.
Отже, в цій точці ряд (1) є абсолютно
збіжним, тобто збіжним є ряд
![]() (3)
(3)
Візьмемо
будь-яку точку![]() ,
тоді в силу вибору
,
тоді в силу вибору![]() ,
матимемо що
,
матимемо що![]() ,
а отже, і
,
а отже, і![]() ,
і для будь-якого
,
і для будь-якого![]() ,
,
![]() .
(4)
.
(4)
З (4) і
збіжності числового ряду (3) за ознакою
Вейерштрасса, маємо рівномірну збіжність
ряду (1) на
![]() .
.
▼
Те, що стверджується в теоремі 2 називають: степеневий ряд рівномірно збіжний всередині інтервалу збіжності (зауважимо, що це зовсім не означає рівномірну збіжність степеневого ряду на інтервалі збіжності).
З попередніх теорем випливає наступний факт.
Теорема3. Сума степеневого ряду (1) є функцією неперервною на всьому інтервалі збіжності.
Для того, щоб застосувати для степеневого ряду дві інші загальні властивості функціональних рядів, спробуємо вирішити наступну проблему.
Очевидно,
якщо ми утворимо ряд з похідних ряду
(1), то одержимо знову степеневий ряд (з
іншими коефіцієнтами). З’ясуємо яким
буде радіус збіжності новоутвореного
ряду. Нехай радіус збіжності ряду (1)
дорівнює
![]() .
Утворимо ряд з похідних ряду (1)
.
Утворимо ряд з похідних ряду (1)
![]() (5)
(5)
і знайдемо
радіус його збіжності. Для цього обчислимо
![]() ,
а це означає, що радіуси збіжності рядів
(1) і (5) співпадають. Отже, ми з’ясували,
що ряд який утворюється з ряду (1) почленним
його диференціюванням є степеневим
рядом з тим самим радіусом збіжності.
,
а це означає, що радіуси збіжності рядів
(1) і (5) співпадають. Отже, ми з’ясували,
що ряд який утворюється з ряду (1) почленним
його диференціюванням є степеневим
рядом з тим самим радіусом збіжності.
Теорема4.
Якщо радіус збіжності ряду (1) не дорівнює
нулю, то для будь-якого
![]() справедлива рівність
справедлива рівність![]() ,
тобто степеневий ряд можна почленно
диференціювати на всьому інтервалі
збіжності.
,
тобто степеневий ряд можна почленно
диференціювати на всьому інтервалі
збіжності.
▲
Візьмемо
будь-яке![]() і довільний відрізок
і довільний відрізок![]() ,
якому належить точка
,
якому належить точка![]() ,
і який міститься в інтервалі збіжності.
А далі до цього відрізка застосуємо
теорему2 і те, що радіус збіжності ряду
з похідних теж дорівнює
,
і який міститься в інтервалі збіжності.
А далі до цього відрізка застосуємо
теорему2 і те, що радіус збіжності ряду
з похідних теж дорівнює![]() .
В результаті одержимо теорему 4.
.
В результаті одержимо теорему 4.
▼
Теорема4’. Степеневий ряд з відмінним від нуля радіусом збіжності можна почленно диференціювати на інтервалі збіжності довільну кількість разів, причому справедливі рівності
![]() ,
,
![]() ,
,![]() ,…
,…![]() ,...
,...
Рівності теореми 4’ легко одержуються з відповідних рівностей продиференційованих рядів.
Зауважимо, що коефіцієнти степеневого ряду з відмінним від нуля радіусом збіжності виражаються через значення суми цього ряду лише в точці, що є центром інтервалу збіжності.
Сума степеневого ряду з відмінним від нуля радіусом збіжності є функція, яка безліч разів диференційована на всьому інтервалі збіжності.
Тепер
розглянемо проблему інтегрування
степеневого ряду. Нехай знову маємо ряд
(1) з відмінним від нуля радіусом збіжності.
Візьмемо точку
![]() ,
тоді відрізок
,
тоді відрізок![]() належатиме інтервалу збіжності. За
теоремою 2, на цьому відрізку ряд (1) буде
рівномірно збіжним. Оскільки, члени
ряду (1) є функції інтегровні на
належатиме інтервалу збіжності. За
теоремою 2, на цьому відрізку ряд (1) буде
рівномірно збіжним. Оскільки, члени
ряду (1) є функції інтегровні на![]() ,
то ряд можна почленно інтегрувати по
цьому відрізку і матимемо, що
,
то ряд можна почленно інтегрувати по
цьому відрізку і матимемо, що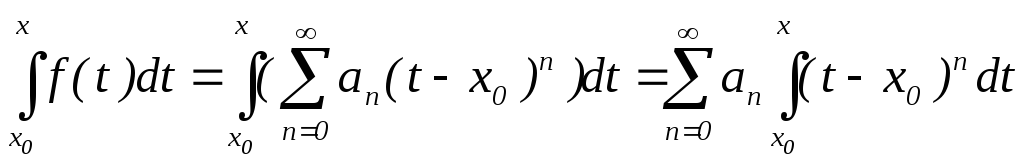 .
Очевидно, що ряд справа в останній
рівності теж буде степеневим рядом,
радіус збіжності, якого буде співпадати
з радіусом збіжності ряду (1).
.
Очевидно, що ряд справа в останній
рівності теж буде степеневим рядом,
радіус збіжності, якого буде співпадати
з радіусом збіжності ряду (1).
Оскільки,
члени степеневого ряду є простими
функціями, з добре відомими властивостями,
то використовуючи ці властивості, а
також характер збіжності, ми можемо
вивчати певні властивості і суми цього
ряду на інтервалі збіжності. В зв’язку
з цим виникає проблема: чи можна, а якщо
так, то як, за заданою, на певному проміжку
функцією, підібрати степеневий ряд так,
щоб ця функція була сумою степеневого
ряду? Якщо така ситуація здійснима для
функції
![]() ,
то кажуть, що цю функцію розкладено у
степеневий ряд. Найближчою нашою
проблемою буде зобразити цю функцію у
вигляді суми степеневого ряду.
,
то кажуть, що цю функцію розкладено у
степеневий ряд. Найближчою нашою
проблемою буде зобразити цю функцію у
вигляді суми степеневого ряду.
