
- •Міністерство освіти і науки україни
- •Розділ і електронні підручники як засіб підтримки учбового процесу
- •Розділ іі технологія створення електронного підручника
- •1. Інструментальне забезпечення. Редактор FrontPage
- •1.1 Вставка тексту
- •1.2 Використання спеціальної вставки
- •1.3 Виділення тексту
- •1.4 Копіювання
- •1.5 Видалення тексту
- •1.6 Розриви тексту
- •1.7 Шаблони
- •1.8 Шаблони сайтів
- •1.9 Шаблони сторінок
- •1.10 Створення фреймів
- •1.11 Шрифти
- •1.12 Символи
- •1.13 Форматування абзаців
- •1.14 Списки
- •1.15 Створення гіперпосилань
- •1.16 Графічні формати
- •1.17 Збереження зображень
- •1.18 Колекція ілюстрацій
- •2 Характеристика та етапи створення електронного підручника
- •Розділ ііі ряди Числові ряди.
- •1.2 Знакододатні ряди. Умови збіжності таких рядів.
- •1.3 Абсолютно та умовно збіжні ряди
- •1.4 Ознаки збіжності знакозмінних рядів.
- •1.5 Множення рядів
- •Функціональні послідовності та ряди
- •2.1 Збіжність, рівномірна збіжність функціональних рядів і послідовностей
- •2.2 Властивості рівномірно збіжних послідовностей і рядів
- •Степеневі ряди
- •3.1 Область збіжності степеневого ряду. Властивості сум степеневих рядів
- •3.2 Розклад функції у степеневий ряд. Біноміальний ряд
- •Висновок
- •Список використаної літератури
2.2 Властивості рівномірно збіжних послідовностей і рядів
Нагадаємо, що раніше ми довели таке твердження.
Теорема1.
(Про неперервність границі рівномірно
збіжної послідовності). Якщо
![]() для
для![]() неперервні на
неперервні на![]() і
і![]() – рівномірно збіжна на
– рівномірно збіжна на![]() до функції
до функції![]() ,
то
,
то![]() – неперервна на
– неперервна на![]() .
.
Теорема1”.
(Про неперервність суми рівномірно
збіжного ряду). Сума рівномірно збіжного
на
![]() ряду, неперервних на цьому відрізку
функцій є неперервною функцією на
ряду, неперервних на цьому відрізку
функцій є неперервною функцією на![]() .
.
Те що виражає теорема 1” символічно може бути записано так:
![]()
Остання рівність показує, що в умовах теореми 1” символи границі і суми можна міняти місцями.
В зв’язку з цими результатами виникає питання: а чи не мають місце аналогічні твердження для похідної та інтеграла Рімана? Тобто, чи вірно, що:
![]() ,
(1)
,
(1)
![]() .
(2)
.
(2)
Що
стосується справедливості рівностей
(1) і (2), то вони, взагалі кажучи, не вірні.
Це можна підтвердити прикладами. Якщо
![]() ,
то легко перевірити, що
,
то легко перевірити, що![]() ,
,![]() ,
,![]() .
При цьому, (що теж легко перевірити) дана
послідовність збігається на
.
При цьому, (що теж легко перевірити) дана
послідовність збігається на![]() нерівномірно. Проте, справедлива наступна
теорема про можливість граничного
переходу під знаком інтеграла Рімана.
нерівномірно. Проте, справедлива наступна
теорема про можливість граничного
переходу під знаком інтеграла Рімана.
Теорема2.
Нехай
![]() – послідовність рівномірно збіжна на
– послідовність рівномірно збіжна на![]() до функції
до функції![]() .
Якщо всі функції
.
Якщо всі функції![]() – інтегровані за Ріманом на
– інтегровані за Ріманом на![]() ,
то
,
то![]() теж інтегрована за Ріманом на
теж інтегрована за Ріманом на![]() і справедлива рівність
і справедлива рівність
![]() (3)
(3)
▲
Для доведення цієї теореми потрібно показати, що:
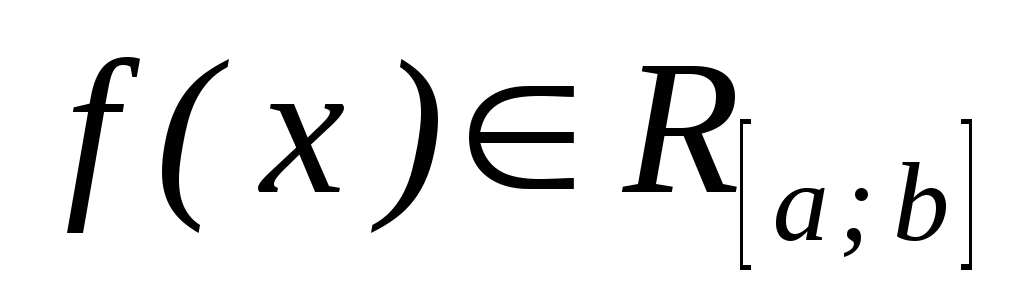 (тут
(тут
 – множина функцій інтегрованих за
Ріманом на
– множина функцій інтегрованих за
Ріманом на );
);справедливість рівності (3).
1) З
критерію інтегрованості за Ріманом,
випливає, що для доведення першої умови,
потрібно встановити, що для
![]() розбиття відрізка
розбиття відрізка![]()
![]() .
(4)
.
(4)
З того,
що послідовність
![]() – рівномірно збіжна на
– рівномірно збіжна на![]() до функції
до функції![]() ,
матимемо що
,
матимемо що
![]() .
(5)
.
(5)
Візьмемо
![]() розбиття відрізка
розбиття відрізка![]() ,
і нехай
,
і нехай![]() – будь-який відрізок цього розбиття.
Виберемо далі довільні дві точки
– будь-який відрізок цього розбиття.
Виберемо далі довільні дві точки![]() та
та![]() з
з![]() ,
і розглянемо різницю
,
і розглянемо різницю![]() .
.![]()
![]()
![]() ,
де
,
де![]() ,
а
,
а![]() .
Проаналізувавши одержану нерівність
(звернувши увагу, що права її частина
не залежить від
.
Проаналізувавши одержану нерівність
(звернувши увагу, що права її частина
не залежить від![]() та
та![]() )
робимо наступний висновок: множина
чисел
)
робимо наступний висновок: множина
чисел![]() обмежена зверху, а отже, існує її
обмежена зверху, а отже, існує її![]() ,
який буде дорівнювати
,
який буде дорівнювати![]() і маємо нерівність
і маємо нерівність
![]() .
(6)
.
(6)
Помноживши
(6) на
![]() ,
і врахувавши, що таких нерівностей буде
,
і врахувавши, що таких нерівностей буде![]() , то після додавання їх усіх, ми одержимо
наступне,
, то після додавання їх усіх, ми одержимо
наступне,![]() ,
або
,
або
![]() .
(7)
.
(7)
Оскільки,
![]() ,
то за критерієм інтегрованості за
Ріманом для вказаного вище
,
то за критерієм інтегрованості за
Ріманом для вказаного вище![]()
![]() розбиття відрізка
розбиття відрізка![]()
![]() .
Звідси і з (7) одержуємо, що
.
Звідси і з (7) одержуємо, що![]() ,
а це означає, що
,
а це означає, що![]() і перша частина теореми доведена.
і перша частина теореми доведена.
2) Для
доведення (3) розглянемо різницю
![]()
![]() ,
а це і означає, що
,
а це і означає, що![]() і (3) доведено.
і (3) доведено.
▼
Теорема2”.
(Про можливість поленого інтегрування
ряду). Нехай
![]() ,
,![]() .
Якщо ряд
.
Якщо ряд![]() рівномірно збіжний до
рівномірно збіжний до![]() на відрізку
на відрізку![]() ,
то
,
то![]() ,
і справедлива рівність
,
і справедлива рівність![]() .
.
Далі потрібно розглянути проблему можливості по членного диференціювання послідовності і ряду. Для доведення теорем нам потрібне одне твердження, яке тісно зв’язане з теоремою про рівномірну збіжність і неперервність.
Теорема3.
Нехай
![]() - рівномірно збіжна на множині
- рівномірно збіжна на множині![]() до функції
до функції![]() послідовність і
послідовність і![]() – гранична точка множини
– гранична точка множини![]() .
Якщо
.
Якщо![]() існує
існує
![]() ,
(8)
,
(8)
то:
існує
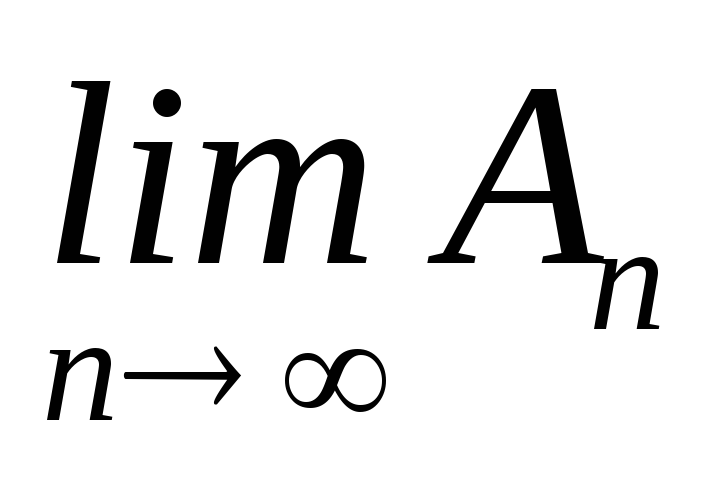 ;
;існує
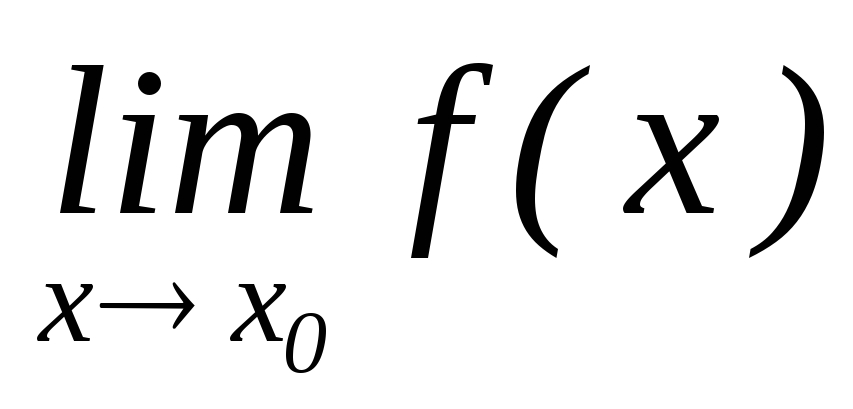 ;
;справедлива рівність
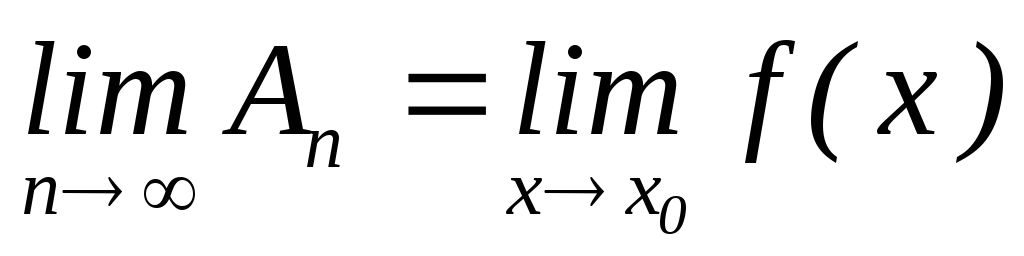 .
.
▲
З умови теореми маємо, що:
![]() .
(9)
.
(9)
Перейшовши
в (9) до границі при
![]() ,
з використанням (8) отримаємо:
,
з використанням (8) отримаємо:![]() ,
а це, за критерієм Коші для числових
послідовностей означає, що існує
,
а це, за критерієм Коші для числових
послідовностей означає, що існує
![]() .
(10)
.
(10)
Розглянемо різницю
![]() (11)
(11)
З того,
що послідовність
![]() – рівномірно збіжна на множині
– рівномірно збіжна на множині![]() до функції
до функції![]() і з умов (8) та (10) матимемо, що
і з умов (8) та (10) матимемо, що![]() ,
для
,
для![]() і
і![]() та
та![]() .
Взявши в (11) довільне
.
Взявши в (11) довільне![]() і
і![]() ,
та використавши три останні нерівності,
одержимо, що
,
та використавши три останні нерівності,
одержимо, що![]() ,
а це означає, що
,
а це означає, що![]() .
.
▼
До речі, з цієї теореми можна ще раз одержати доведену вище теорему1.
Тепер вже можна розглянути проблему граничного переходу під знаком похідної. Зауважимо тільки, що якщо вимагати навіть рівномірної збіжності послідовності чи ряду, то цього виявиться замало для справедливості рівності (2).
Теорема4.
(Про граничний перехід під знаком
похідної). Нехай про послідовність
![]() відомо наступне:
відомо наступне:
існує точка
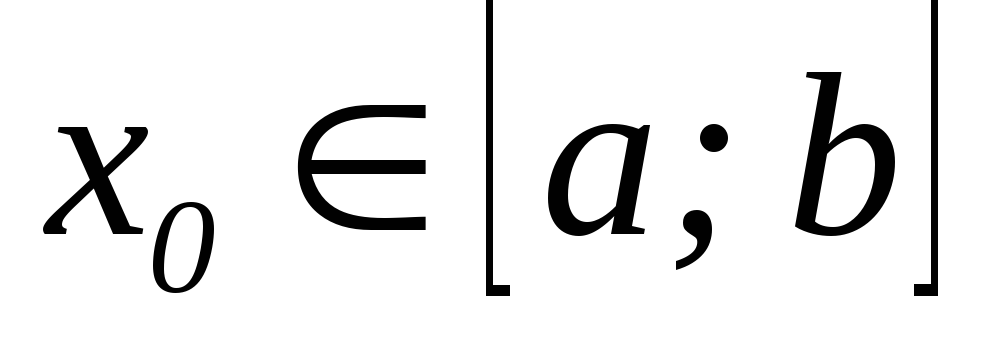 ,
така, що
,
така, що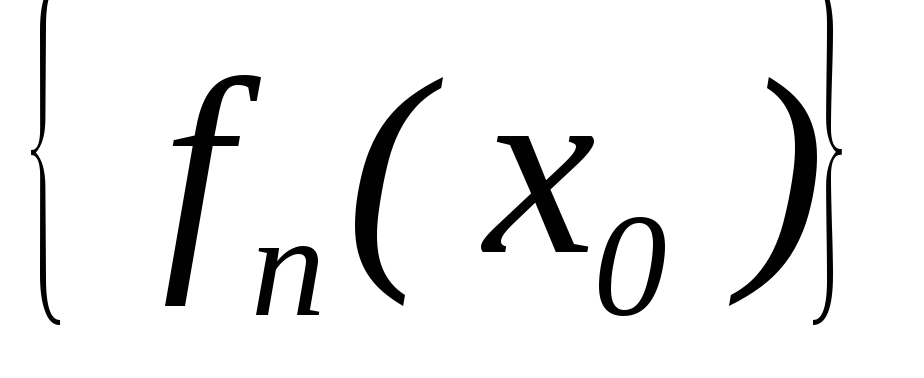 – збіжна;
– збіжна;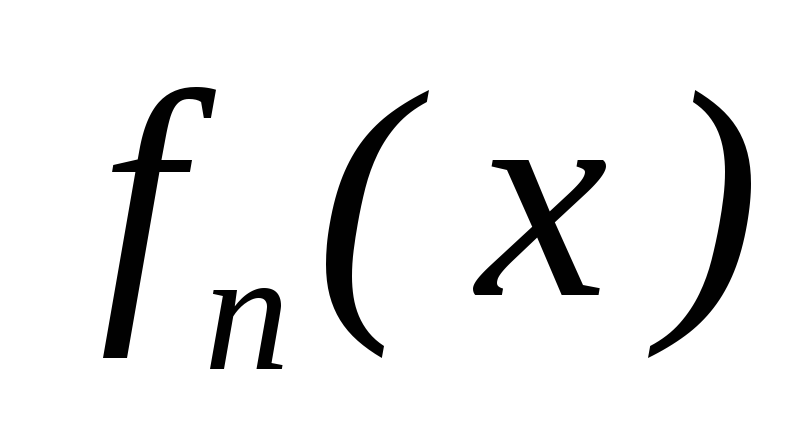 для
для
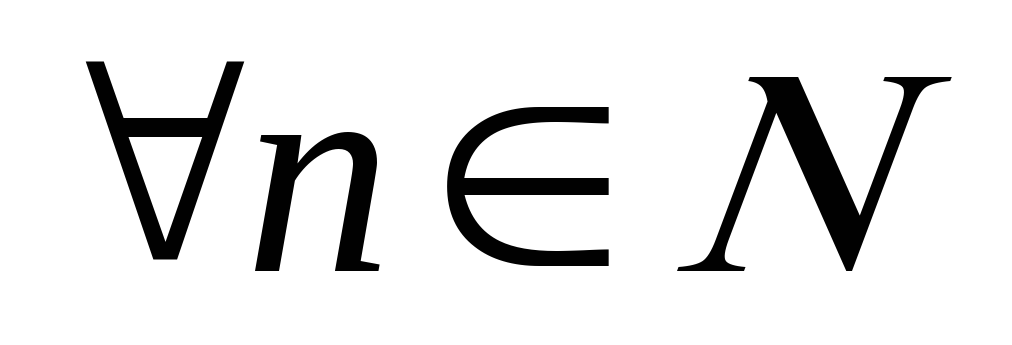 – диференційовані на
– диференційовані на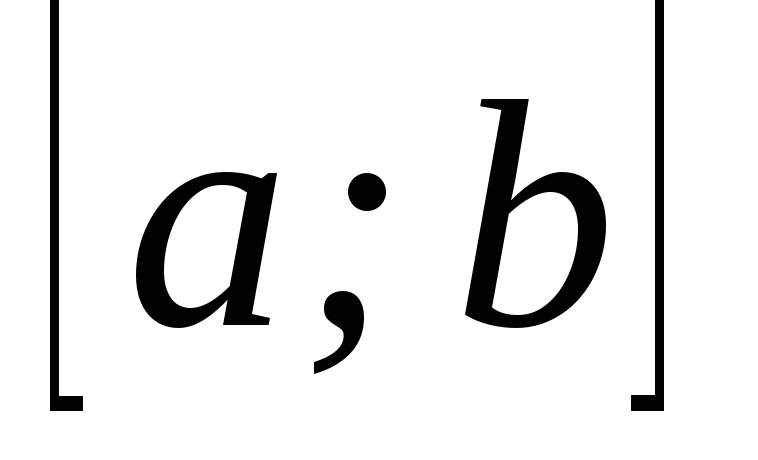 функції;
функції;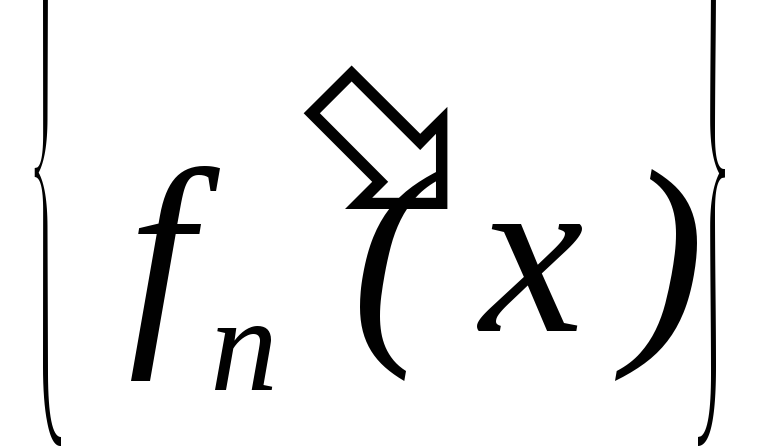 –рівномірно
збіжна на
–рівномірно
збіжна на
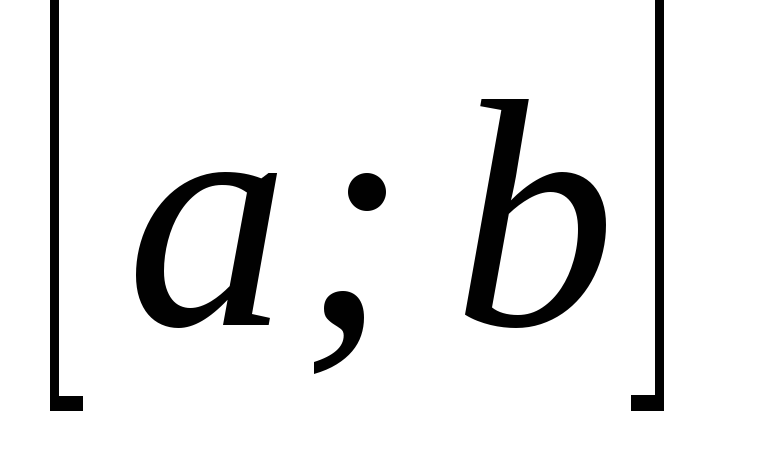 послідовність.
послідовність.
Тоді:
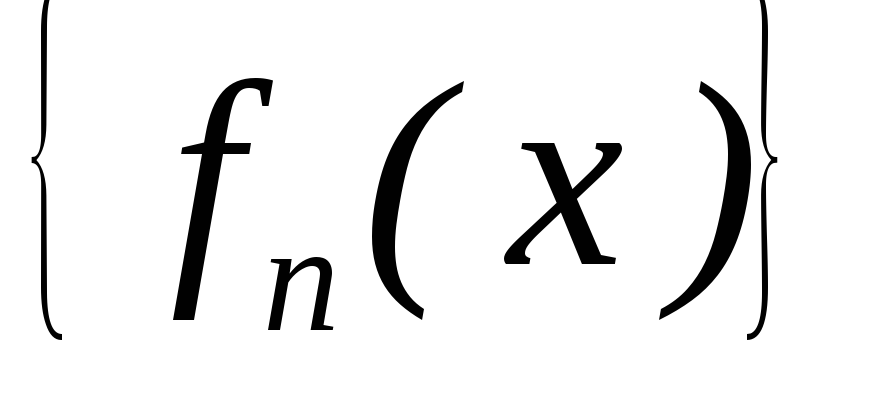 –рівномірно
збіжна до деякої функції
–рівномірно
збіжна до деякої функції
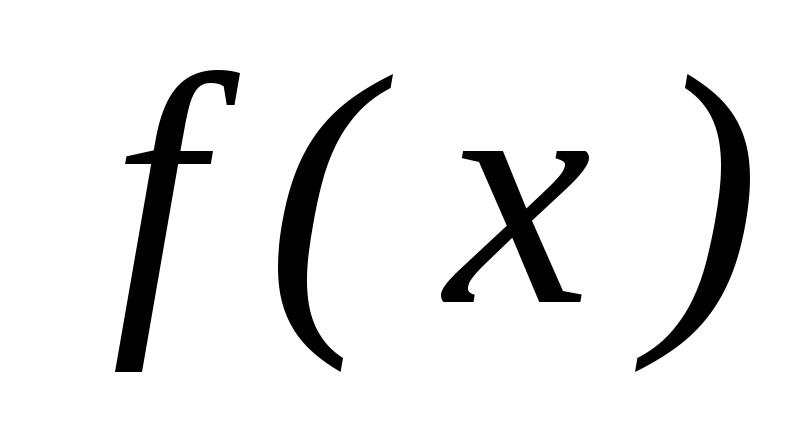 на
на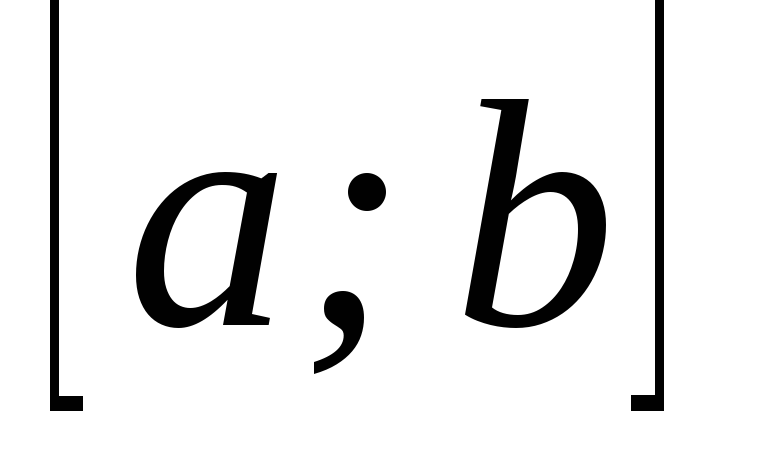 послідовність;
послідовність;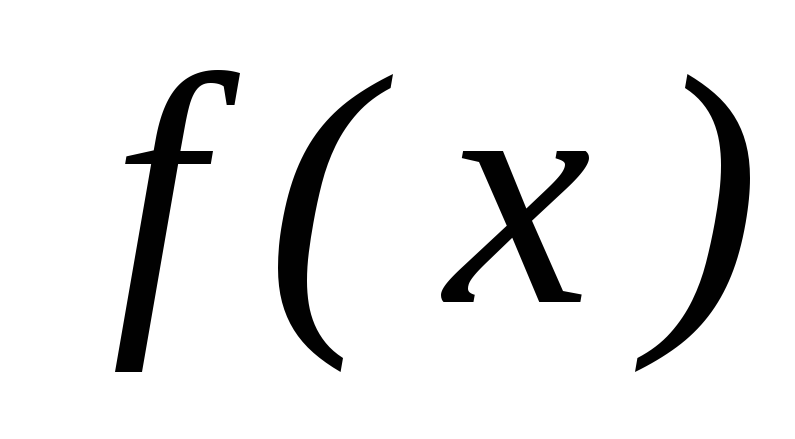 –диференційована
на
–диференційована
на
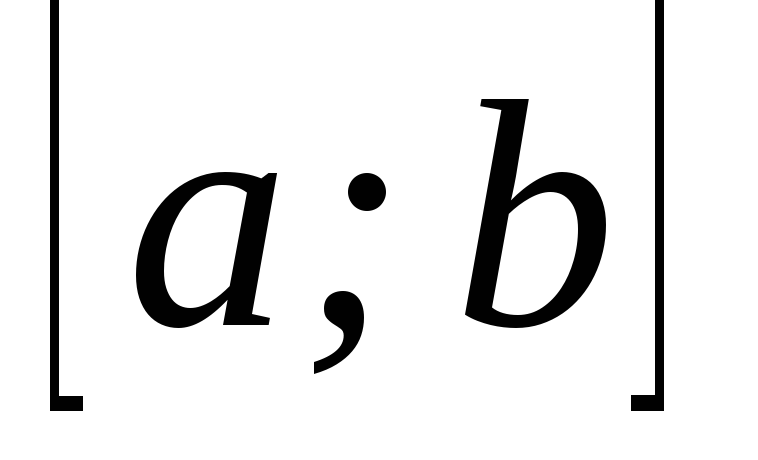 ;
;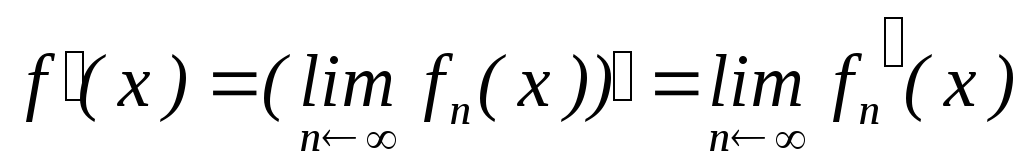 для
для
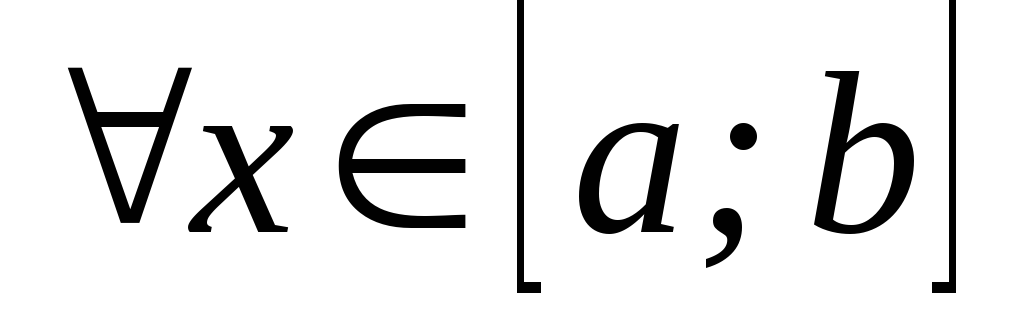 .
.
▲
Проаналізувавши формулювання цієї теореми і теореми про по членне інтегрування, можемо зробити висновок, що для граничного переходу під знаком похідної слід накладати серйозніші умови, ніж ті, які потрібні для граничного переходу під знаком інтеграла.
Доведемо спочатку умову а). Для цього з умов теореми матимемо, що
![]() ,
(12)
,
(12)
![]() .
(13)
.
(13)
Розглянемо
далі таку функцію
![]() на проміжку з кінцями
на проміжку з кінцями![]() і
і![]() ,
де
,
де![]() і
і![]() – будь-які точки з відрізка
– будь-які точки з відрізка![]() .
Зрозуміло, що введена вище функція, на
цьому відрізку буде задовольняти всім
умовам теореми Лагранжа. Тоді, матимемо,
що між
.
Зрозуміло, що введена вище функція, на
цьому відрізку буде задовольняти всім
умовам теореми Лагранжа. Тоді, матимемо,
що між![]() і
і![]() існує
існує![]() ,
таке що
,
таке що
![]() .
(14)
.
(14)
Звідси і з (13) матимемо,
![]() .
(15)
.
(15)
Далі
для
![]() оцінимо таку величину
оцінимо таку величину![]() ,
,![]()
![]() ,
а це (за критерієм Коші) означає, що
послідовність
,
а це (за критерієм Коші) означає, що
послідовність![]() – рівномірно збіжна на
– рівномірно збіжна на![]() до деякої функції
до деякої функції![]() .
.
Для
подальшого доведення теореми введемо
в розгляд наступні функції. Спочатку
візьмемо
![]() і зафіксуємо її. Позначимо через
і зафіксуємо її. Позначимо через![]() і
і![]() на множині
на множині![]() .
Із (15) випливає
.
Із (15) випливає
![]() ,
(15)”
,
(15)”
або
згадавши означення функції
![]() одержуємо, що
одержуємо, що![]() .
Останнє співвідношення, разом з вимогами
накладеними на
.
Останнє співвідношення, разом з вимогами
накладеними на![]() ,
,![]() і
і![]() ,
означає що
,
означає що![]() – рівномірно збіжна до
– рівномірно збіжна до![]() на множині
на множині![]() послідовність, причому точка
послідовність, причому точка![]() для
для![]() є граничною.
є граничною.
Розглянемо
границю
![]() ,
бо функція
,
бо функція![]() диференційована на
диференційована на![]() ,
значить і в точці
,
значить і в точці![]() .
Щойно одержане
.
Щойно одержане![]() грає роль
грає роль![]() із теореми 3, і отже, виконані всі умови
теореми 3 для
із теореми 3, і отже, виконані всі умови
теореми 3 для![]() на
на![]() .
Згідно цієї теореми матимемо, що:
.
Згідно цієї теореми матимемо, що:
існує
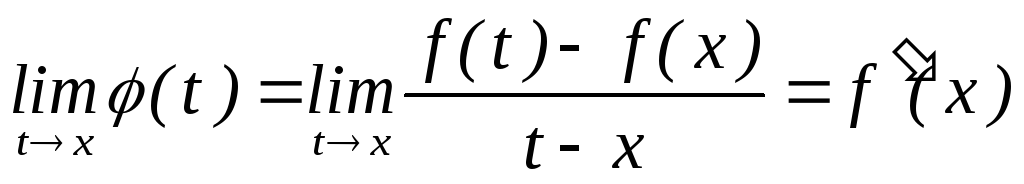 ,
а це означає, що функція
,
а це означає, що функція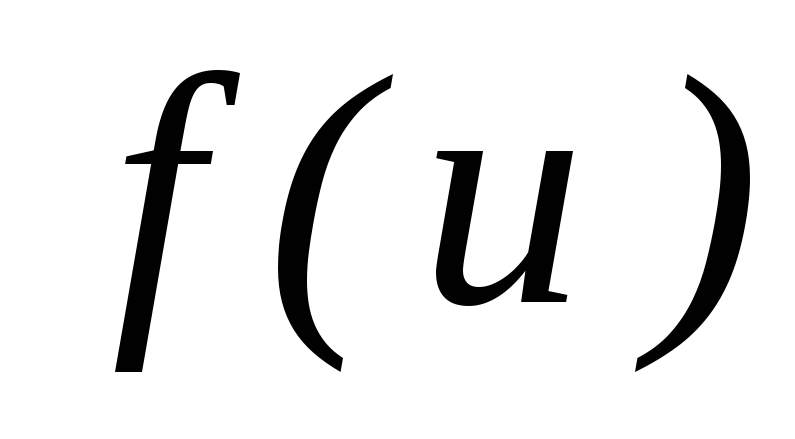 диференційована в точці
диференційована в точці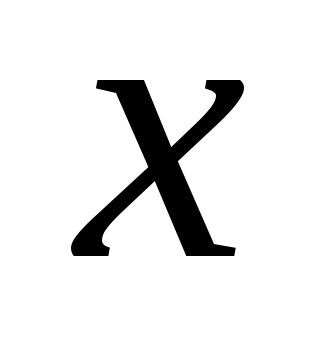 ;
;існує
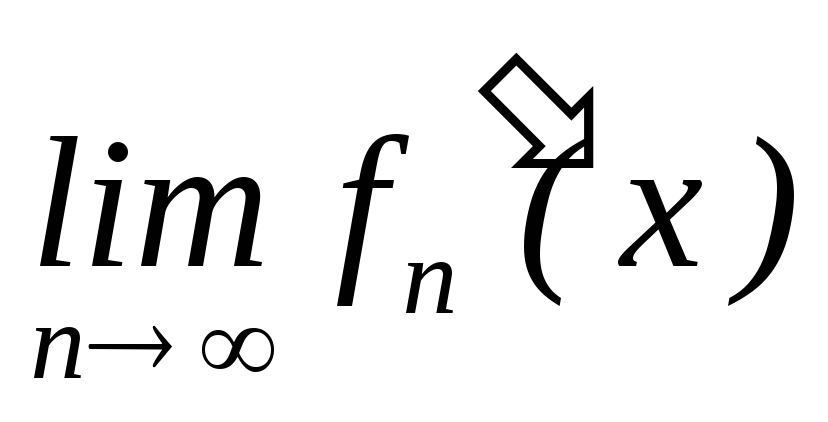 ;
;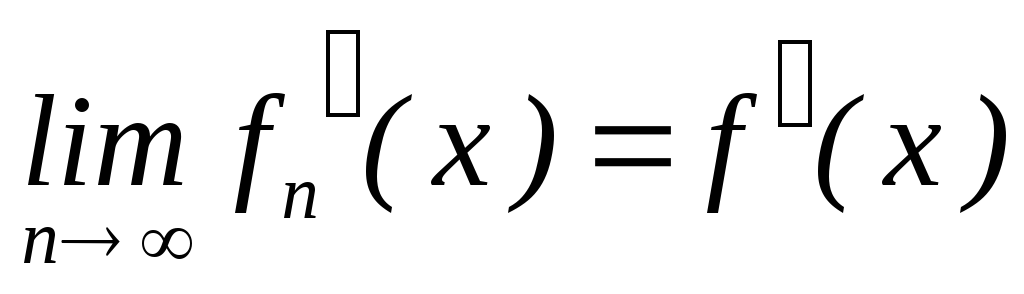 .
.
Оскільки
точка
![]() - довільна з
- довільна з![]() ,
то теорема 4 доведена повністю.
,
то теорема 4 доведена повністю.
▼
Теорема4”.
(Про можливість по членного диференціювання
ряду). Нехай
![]() – ряд, членами якого є диференційовані
на
– ряд, членами якого є диференційовані
на![]() функції. Якщо:
функції. Якщо:
існує точка
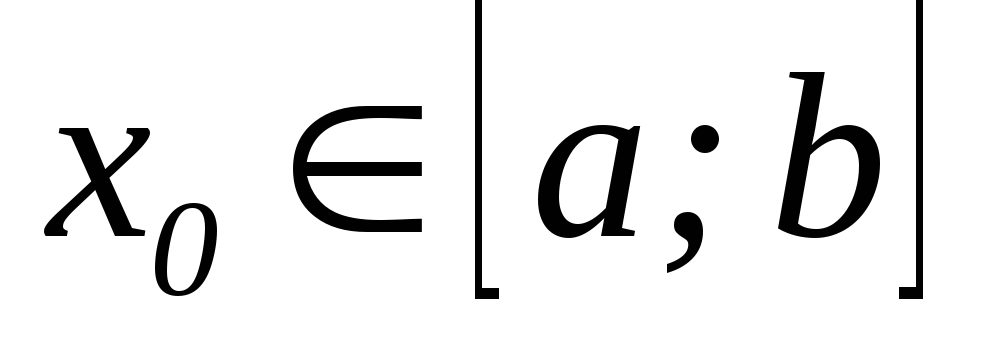 така, що
така, що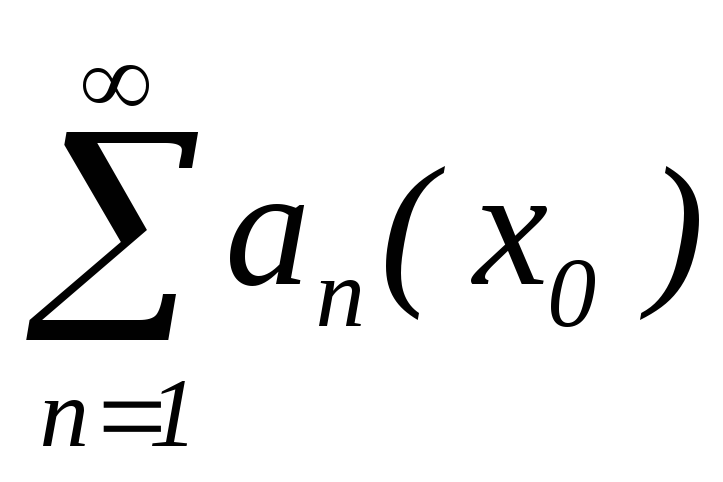 – збіжний;
– збіжний;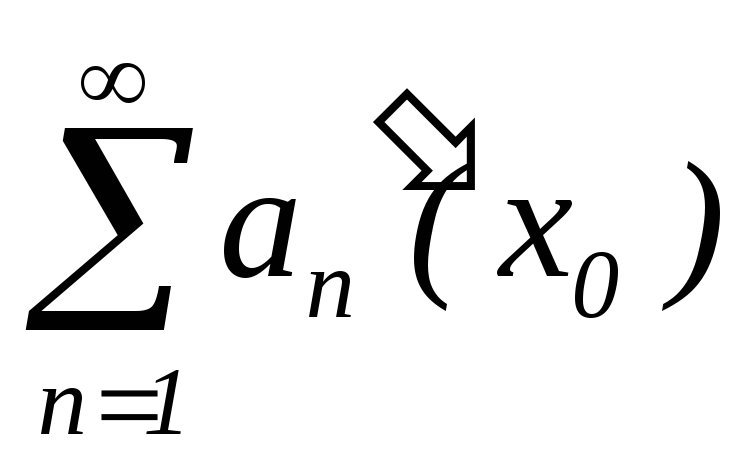 –рівномірно
збіжний на
–рівномірно
збіжний на
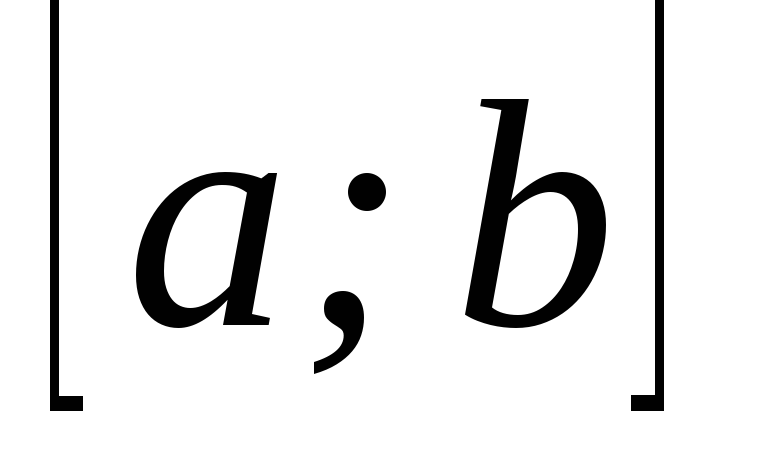 .
.
Тоді:
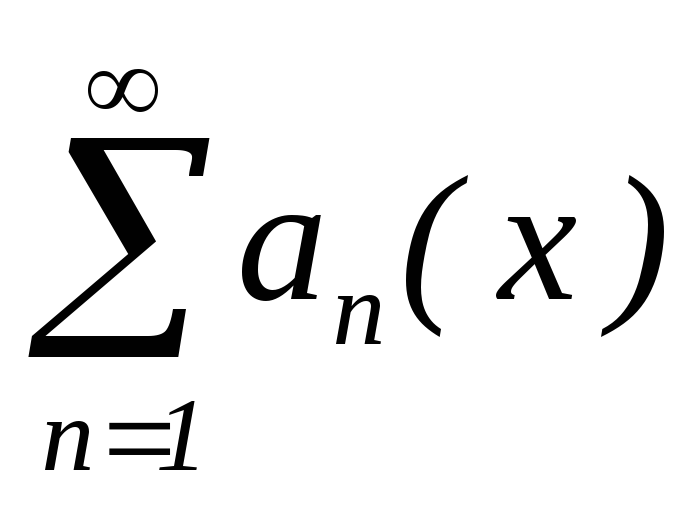 –рівномірно
збіжний на
–рівномірно
збіжний на
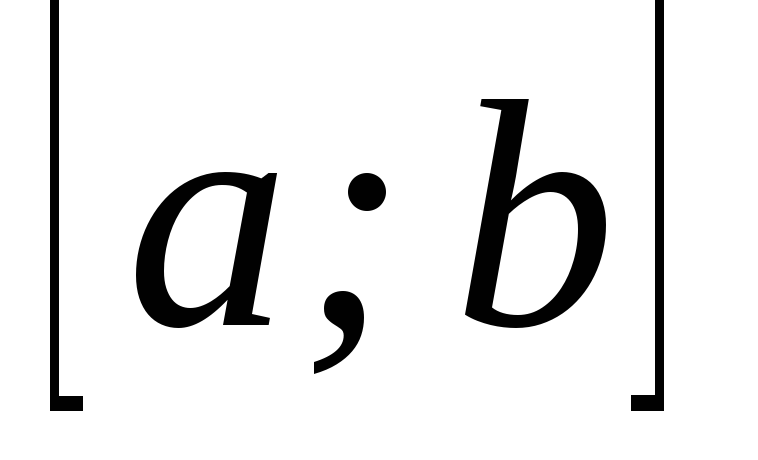 ;
;сума ряду
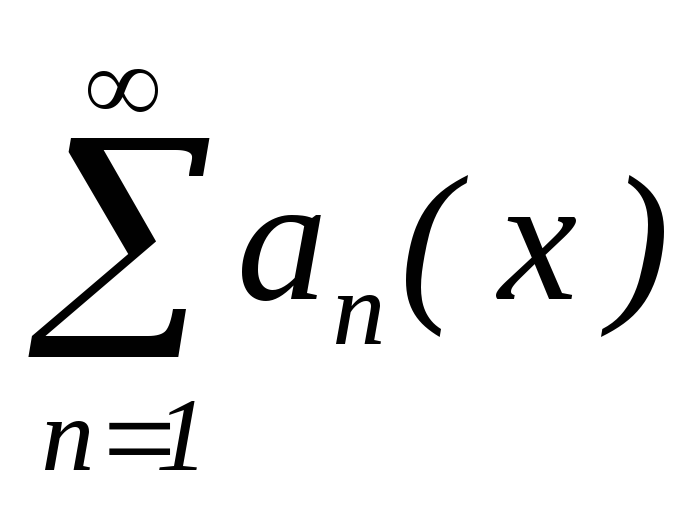 – диференційована на
– диференційована на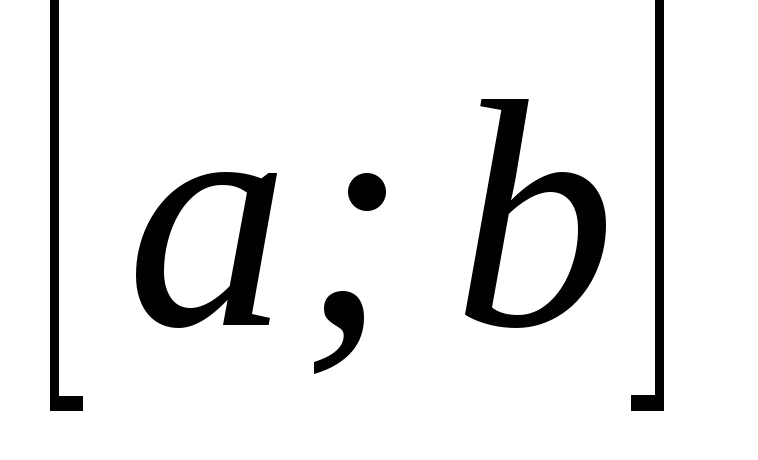 функція;
функція;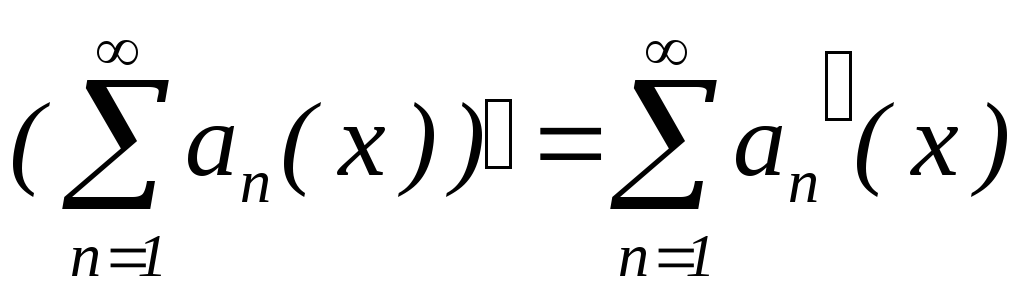 ,
для
,
для
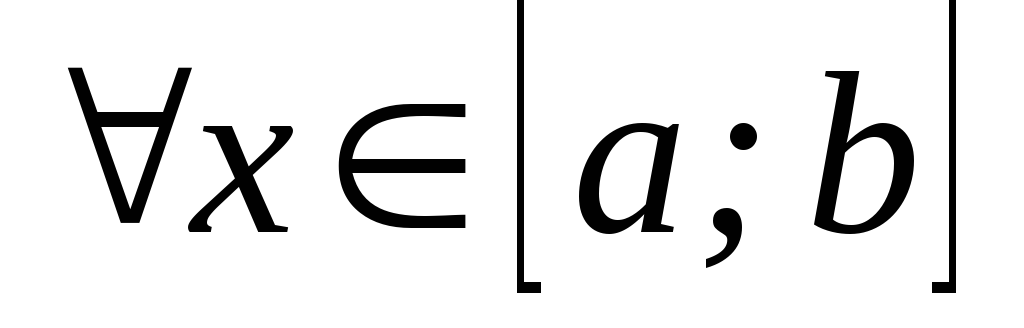 .
.
