15. Функции. Непрерывность функции в точке и в области

Функция f(x) назыв. непрерывной в точке x0, если существует lim(x→x0) f(x), равный значению функции f(x) в этой точке:

lim(x → x0) f(x) = f(x0),

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

Говорят, что функция f (x) имеет точку разр. первого рода при x = a, если в этой точке

1. Сущ. левостор. и правостор. предел

2. Эти односторонние пределы конечны.

Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.

Ф-ция y=f(x) назыв непрерывной в т.x₀, если предел ф-ции в этой точке равен значению ф-ции в этой точке т.е.,

Выполняется условия:

-существует знач. ф-ции в т.x₀

-сущ. конечн. предел в т. x₀

-этот предел равен значению ф-ции f(x₀).

Если в определении непрерывности ф-ции не выполняется хотя бы одно из трёх условий, то ф-ция f(x) не явл. непрерывной в т. x₀ или имеет в этой точке разрыв, а саму т. x₀ назыв. точкой разрыва ф-ции.

Точку x₀ ф-ции f(x) назыв. точкой разрыва первого рода, если оба односторонних предела существуют или конечны. Точку x₀ ф-ции f(x) назыв. точкой разрыва второго рода, если хотя бы один из односторонних предела бесконечны или не существ. вообще.

Точка разрыва предела первого рода назыв. точкой устранённого разрыва, если левый и правый в этой точке равны между собой.

Ф-ция назыв. непрерывной справа, если правый предел равен значению ф-ции:

Очевидно, что ф-ция f(x) непрерывна в т. x₀ тогда, когда она в этой точке одновременно непрерывна справа и слева.

Св-ва непрерывных ф-ций: 1. Сумма двух непрерывных ф-ций есть непрерывная ф-ция. 2. Произведение двух непрерывных ф-ций есть непрерывная ф-ция. 3. Частное двух непрерывных ф-ций есть непрерывная ф-ция, за исключением точек в кот делитель не равен нулю. 4. Если в ф-ции у=f(u) u=f(x) , явл непрерывн ф-ями своих аргументов, то сложн ф-ция y=f(φ(x)) явл непрерывной. Осн. теоремы о непрерыв ф-циях: Теорема Вейерштрассе: Если ф-ция f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке. Теорема Больцана-Коши: Если ф-ция f(x) непрерывна на отрезке [a,b] и на концах разных знаков, то сущ-ет точка такая, что f( )=0.

16. Производная ф-ции. Смысл.

Производной ф-ции y=f(x) в тч. Х₀ наз. предел отношения приращения этой ф-ции к приращению аргумента , когда последнее стремится к нулю.

Формулавыражаетгеометрический смысл производной: производная от данной ф. в данной точке = tg угла наклона касательной графика ф-ции в этой тчк. Производительность труда есть производная объема продукции по времени. Рассмотрим некоторые понятия, иллюстрирующие экономический смысл производной. Пусть y(x) – ф-ция, характеризующая, например, издержки производства, где x - количество выпускаемой продукции. Тогда отношение 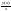описывает средние издержки, приходящиеся на одно изделие. Средняя величина обозначается Ay или Af (от английского "average".) Среднее приращение, средний прирост, средняя скорость изменения определяется отношением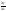. 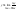Производнаявыражает предельные издержки производства. Величину Mf(x) = y' наз. мгновенным приростом или мгновенной скоростью изменения y. Аналогично можно определ. предельную выручку, предельный доход, предельную полезность и др. предельные величины.

Правила дифференцирования: 1.Производная сум.(разности) двух дифференц-ых ф-ций =сумме(разности) производных этих ф-ций

2.Производная произведения двух диффиренц-ых ф-ций = произведению первой ф-ции на роизводную второй + произведение второй ф-ции на производную первой:

3.Производная частного двух дифференц-ых ф-ций определ. формулой: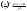

где