7. Векторы. Сложение, вычитание векторов, умножение вектора на число.

Вектор – это объект, кот.имеет длину и направление. Это пара точек, про кот.известно, какая является началом, а какая концом.

Векторы бывают: 1) свободными (начало несущественно для рассмотрения задачи, их можно переносит пар-но самому себе как угодно.) 2) связанными (начало существенно для рассмотрениязадачи).

Длина вектора обозначается: |AB|

Если начало и конец совпад, то вектор наз-ся нулевой. Его направление считается неопределенным.

Сложение векторов: по правилу параллелограмма.

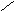
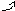
Умножение вектора на число: результатом умножения свобод.вектора на положительное число 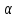будет вектор, имеющий то же направление, что и исходный, но с длиной в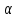раз больше.

8. Операции над векторами, заданными в координатной форме.

Равенство векторов и линейные операции (сложение векторов и умножение вектора на число) удобно представлять в координатной форме. При этом справедливы следующие свойства.

1. Равные векторы имеют равные координаты (в одном и том же базисе).

2. Каждая координата суммы векторов равна сумме соответствующих координат слагаемых.

3. Каждая координата произведения вектора на число равна произведению этого числа на соответствующую координату вектора.

4. Каждая координата линейной комбинации векторов равна линейной комбинации соответствующих координат векторов.

Вектора можно:

1. Складывать и вычитать.

2. Умножать на число.

3. Искать их скалярное произведение.

4. Искать угол между векторами.

9. Скалярное произведение векторов, его свойства.

Скал.произведение (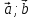) – число, равное произвед.длин этих векторов наcos угла между ними.

Свойства скал.произведения:

1.Не зависит от порядка умножения.

2.Скал.произведение вектора на самого себя = квадрату этого вектора.

3.Скал.произведение взаимоперпендикулярных векторов = 0.

10. Векторное произведение векторов, его свойства.

Векторное произвед.векторов – операция над ними, результатом кот.явл-ся вектор, обладающий след.свойствами:

1.Векторное произвед.вектора на самого себя = 0.

2.Постоянный множитель можно выносить за знак векторного произведения.

3. [] = [;

[] = ([) + []

[] =[] + []

=

=

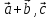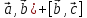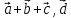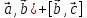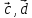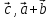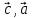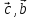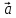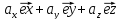
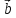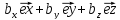
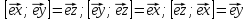–правые тройки векторов.

Если в декартовой системе координат 1 напр-е изменилось на противоположное, то получается левая тройка векторов.

Смысл векторного произвед.: длина векторного произв. 2х векторов = площади параллел-ма, построенного на этих векторах:

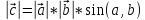
11. Системы линейных алгебраических уравнений. Решение их методами Гаусса, Крамера, матричным.

Метод Гаусса: Процедура решает неоднородную систему n линейных алгебраических уравнений с n неизвестными: a₁₁ x₁+a₁₂ x₂+ . . .+a_1n x_n=a_1n+1

a₂₁ x₁+a₂₂ x₂+ . . .+a_2n x_n=a_2n+1 . .

a_n1 x₁+a_n2 x₂+ . . .+a_nn x_n=a_nn+1

Вначале находим отличный от нуля коэффициент при x₁. Соответствующее уравнение переставляем с первым (если это необходимо). Получаем систему с a₁₁ отличным от нуля. Разделив коэффициенты этого уравнения на a₁₁, получим:

x₁+b₁₂ x₂+ . . .+b_1n x_n=b_1n+1

При помощи этого уравнения исключаем x₁ из исходной системы:

a⁽¹⁾₂₂ x₂+a⁽¹⁾₂₃ x₃+ . . .+a⁽¹⁾_2n x_n=a⁽¹⁾_2n+1 .

a⁽¹⁾_n2 x₂+a⁽¹⁾_n3 x₃+ . . .+a⁽¹⁾_nn x_n=a⁽¹⁾_nn+1

где

a⁽¹⁾_{i j}=a_{i j}-a_{i 1}b_{1 j}, i,j= 2...n

Полученная система содержит n-1 уравнение. Применяем описанную выше процедуру к этой системе. Операции повторяем требуемое число раз, пока не приведем систему к треугольному виду:

x₁+с₁₂ x₂+ . . .+с_1n x_n=с_1n+1

x₂+ . . .+c_2n x_n=c_2n+1

x_n=c_nn+1

Теперь легко определить x_n,x_n-1, . . ., x₁.

Если det(A)=0, то исходная система не имеет решений и процедура выдает S=0 иначе S=1 и решения находятся в массиве X.

Метод Крамера: каждый из неизвестных x – дробь, в знаменателе кот.нах-ся определитель системы, а в числителе определитель, получ.из определителя системы путем замены столбца, №кот. = № x на столбц свободных членов. a₁₁ x₁+a₁₂ x₂+ . . .+a_1n x_n=a_1n+1

a₂₁ x₁+a₂₂ x₂+ . . .+a_2n x_n=a_2n+1 . .

a_n1 x₁+a_n2 x₂+ . . .+a_nn x_n=a_nn+1

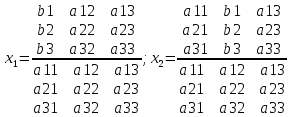
Матричный метод:

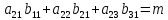
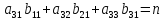
Пусть знаменатель = =

А числитель = D. Для =

==

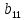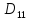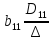. Для остальных – аналогично.