46. Дифференциальные уравнения (основные понятия)

Дифференциальным уравнением наз-ся уравнение относительно неизвестной ф-ии и ее производных различных порядков. Порядком дифференциального урав.назыв-ся порядок старшей производной ,входящей в это уравнение.

Решением диф.ур-ния порядка n наз-ся функция y(x), имеющая на некот.интервале (a,b) производные

 до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием.

В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные.

Решения дифференциальных уравнений подразделяются на общие и частные решения. Общие решения включают в себя неопределенные постоянные, а для уравнений в частных приозводных — произвольные функции от независимых переменных, которые могут быть уточнены из дополнительных условий интегрирования (начальных условий для обыкновенных дифференциальных уравнений, начальных и граничных условий для уравнений в частных производных). После определения вида указанных постоянных и неопределенных функций решения становятся частными.

47. Дифференциальные ур-я 1-го порядка с разделяющимися переменными:

Дифференциальным уравнением 1-го порядка с разделяющимися переменными называется уравнение вида: P(x)dx+Q(y)dy=0 (1). Его общим интегралом будет: 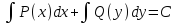(2). Уравнение вида: M₁(x)·N₁(y)dx+M₂(x)·M₂(y)dy=0 (3), а также уравнение вида: y'=f₁(x)·f₂(y) (4) уравнения, которые с пом. алгебраических преобразований приводятся к ур-ям (3) или (4) наз. ур-ми с разделяющимися переменными. Рассмотрим ур-е (3). Допустим, что N₁(y)·M₂(x)≠0. Разделим обе части ур-я (3) на N₁(y)·M₂(x). Получим: ,

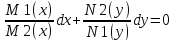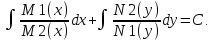Рассмотрим ур-е (4): 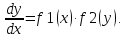Домножим обе части ур-я на dx и разделим на f₂(y) в предположении, что f₂(y)≠0.

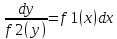
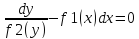
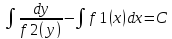–общий интеграл.

Замечание: При выводе общих интегралов ур-ий (3) и (4) сделаем нек. допущения, к-е могут привести к потере решений. Случай, когда M₁(y)·M₂(x)=0 или f₂(y)=0 необходимо рассматривать отдельно, чтобы не потерять возможных решений дифференциальных ур-ий.

48. Однородные дифференциальные уравнения

Однородное дифференциальное уравнение может быть записано в видеили

где , - однородные функции одной и той же степени, т.е. для некоторого натурального числа k и для произвольного справедливы равенства

Для решения однородного дифференциального уравнения необходимо сделать замену переменных , которая сводит однородное дифференциальное уравнение к дифференциальному уравнению с разделяющимися переменными.

49. Линейные дифференциальные уравнения с постоянными коэффициентами

 Уравнение

                       наз. линейным дифференциальным уравнением  n-го порядка с постоянными коэффициентами;  a_k - постоянные вещественные числа.  Если  функция f(x)  не равна тождественно нулю, то иногда говорят, что  уравнение с правой частью. 

 Уравнение

наз. линейным  однородным  дифференциальным ур-го порядка с постоянными коэффициентами;  a_k - постоянные вещественные числа.  Т. к.  функция f(x)  равна тождественно нулю, то иногда говорят, что ур-ние без правой части. 

Уравнение     наз.характеристическим ур-ем, а его корни – характер-ми числами уравнения. 

 Система функций

  наз. линейно независимой в интервале  (a,b), если тождество   (- постоянные числа)

 может выполняться только когда все c_k=0. Если к  тому же каждая из функций   y_k явл. частным решением однородного уравнения , то система решений одно-родного ур-ния наз.  фундамент. системой решений.

Если фундаментальная система решений найдена, то функция

 

дает общее решение однородного уравнения ,  ( все c_k - константы ).