34. Частные производные высших порядков.
Производные второго и более высокого порядков наз. произв-ми высших порядков.
Пусть f ’(x) – производная первого порядка ф-и f(x). Производной второго порядка ф-и f(x) наз. производная от ф-и f ’(x), если она сущ-т. Обозначается вторая произв-я f ’’(x).
Производную от второй производной наз. производной третьего порядка ф-и f(x) и обозначают f ’’’(x).
Произв-я n-го порядка явл-ся произв-й от произв-й (n-1)-го порядка. Она обозначается f (n)(x).
35. Независимость частных производных от порядка дифференцирования.
36. Метод наименьших квадратов.
При обработке опытных данных часто встречаются с задачей об определении параметров функциональной зависимости между переменными величинами x и y посредством формулы y=f(x).Эта задача решается с помощью метода наименьших квадратов, сущность которого состоит в следующем. При измерении двух величин x и y получены следующие данные:
|
x |
Х1 |
X2 |
… |
xn |
|
y |
Y1 |
Y2 |
… |
yn |
Известен также вид функциональной зависимости, т.е.
y=f(x,
,
,…,
)=φ(x)
(1),
где f-заданная
функция;
,
,…,
—
параметры, значения которых требуется
определить. Значения у,
полученные
из формулы (1) при заданных значениях
(i=1,
2,..., п),
как
правило, не совпадают с экспериментальными
значениями
,приведенными
в указанной таблице, т.е. разность
-φ(
)
отлична от нуля для всех или некоторых
точек
(i
= 1, 2, ..., n).
Для каждого i
эту разность обозначим через ε
,
и назовемпогрешностью:
-φ(
)=ε
(i
= 1, 2,..., п)
(2) .
Значения
параметров
(k
=
0, 1,..., m)
функции (1) требуется выбрать так,
чтобы сумма квадратов погрешностей
была наименьшей, т.е. так, чтобы функция
u=
ε
=
(
-φ(
))
(3)
принимала наименьшее значение. Поскольку эта функция - сумма квадратов некоторых чисел, она принимает неотрицательные значении (каждое слагаемое суммы неотрицательно).
Функция
(3) является функцией т+1
переменых
,
,...,
ат
,т.е.
и=и(
,
,
...., ат)=
(
-f(
,
,
,…,
))2
(4).
Если
функция и=и(
,
...,
ат)
имеет
непрерывные частные производные по
всем переменным, то необходимое условие
ее минимума выражается системой
уравнений
=0,
=0,
…,
=0
(5)
Из этой системы т +1 уравнений находятся искомые значения параметров a0,a1 ,...,am.
Во многих случаях функция (1) определяется формулой
y=
(x),
(6)
где
(x),
(x),...,
f
т
(
x
)- известные
функции, например, f
(x)=x
,f
(x)=sin
kx,
f
(x)=cos
kx
и т.д.
Функция (4) в таких случаях принимает вид
u=
y
-
(
))
(7),
а система (5) запишется так:
(
-
(
))(-
(
))=0
(
-
(
))(-
(
))=0(8)
…………………………………….
(
-
(
))(-
(
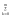
))=0
Решение этой системы может быть получено с помощью метода Гаусса (метод последовательного исключения неизвестных).
Если
(x)=
(k
= 0, 1, 2,..., m),
то
f(x,
,
,…,
)=
+
x+
+…+
+
(9)
и система (8) принимает вид:
n+
+…+
=
;
+
+…+
=
;
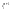(10)
+
+…+
*
*
=
.
