88

Ярославский филиал федерального государственного

бюджетного образовательного учреждения высшего

профессионального образования «Московский государственный

университет экономики, статистики и информатики (МЭСИ)»

Жолудева В.В.

Математика (для студентов заочной формы обучения)

Учебное пособие

Ярославль 2012

УДК

ББК

Жолудева В.В. Математика (для студентов заочной формы обучения): учебное пособие/ В.В.Жолудева, Ярославский филиал МЭСИ. – Ярославль:

Учебное пособие предназначено для организации практических занятий и самостоятельной работы студентов I курса заочной формы обучения по направлениям «Менеджмент» (бакалавриат) и «Экономика» (бакалавриат). Каждая тема содержит теоретический материал, образцы задач с полным, подробным их решением, задания для самостоятельной работы.

Рецензенты: Зиновьев К.А., заведующий кафедрой математики и информационных технологий ФГБОУ ВПО Ярославская ГСХА, профессор, канд. ф.-м. наук

Рассмотрено и рекомендовано к изданию Учебно-методическим советом Ярославского филиала МЭСИ,

© ЯФ МЭСИ, 2012

© Жолудева В.В., 2012

Содержание

Раздел 1. Линейная алгебра………………………………………………………4

1. Матрицы и определители………………………………………4

2. Системы линейных уравнений…………………………..........11

3. Векторные пространства. Арифметические векторы……….16

4. Контрольные задания для студентов по разделу 1 «Линейная алгебра»………………………………………………………...19

Раздел 2. Элементы аналитической геометрии…………………………..........23

2.1 Векторы на плоскости и в пространстве…………………….23

2.2 Аналитическая геометрия на плоскости……………………..27

2.3 Аналитическая геометрия в пространстве…………………...34

2.4 Контрольные задания для студентов по разделу 2 «Элементы аналитической геометрии»…………………………………...36

Раздел 3. Математический анализ. Дифференциальное и интегральное исчисление функции одной переменной………………………..42

3.1 Предел последовательности, предел функции………………42

3.2 Производная функции и ее применение к исследованию функций………………………………………………………..48

3.3 Неопределенный интеграл……………………………………54

3.4 Определенный интеграл. Несобственный интеграл………...56

Раздел 4. Математический анализ. Функции нескольких переменных……...58

4.1 Понятие функции нескольких переменных…………………58

4.2 Дифференциальное исчисление функций нескольких переменных……………………………………………………59

Раздел 5. Математический анализ. Дифференциальные уравнения………….61

5.1 Комплексные числа и действия над ними……………….…..61

5.2 Дифференциальные уравнения первого порядка…………...62

5.3 Дифференциальные уравнения второго порядка…………...66

Раздел 6. Математический анализ. Числовые и степенные ряды…………….69

6.1 Знакоположительные числовые ряды. Признаки сходимости…………………………………………………….69

6.2 Знакочередующиеся числовые ряды. Признак Лейбница.....72

6.3 Степенные ряды……………………………………………….74

6.4 Контрольные задания для студентов по разделам

3 – 6 «Математический анализ»……………………………...76

Раздел 1. Линейная алгебра

1. Матрицы и определители

Прямоугольной матрицей порядка m×n называется таблица чисел, состоящая из m строк и n столбцов.

Сокращенно обозначается .

Числа называются элементами матрицы А.

Если m=n, то матрица называется квадратной, а число n называют порядком матрицы.

Совокупность элементов образует главную диагональ квадратной матрицы, а элементы- побочную диагональ.

Так, для матрицы

главная диагональ – это числа 1, 4, 3, побочная диагональ – 7, 4, 6.

Нулевой матрицей называют матрицу, все элементы которой равны нулю:

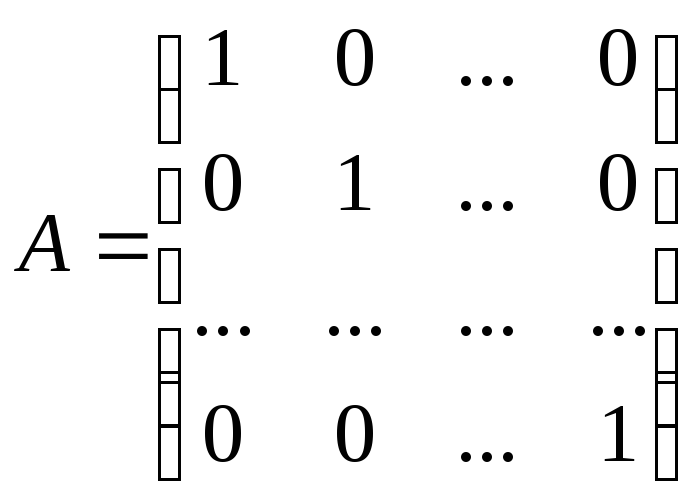
Единичная матрица – это матрица, на главной диагонали которой стоят единицы, все остальные элементы равны нулю:

Квадратная матрица, под главной диагональю которой стоят нули, называется верхнетреугольной; соответственно определяется нижнетреугольная матрица:

- верхнетреугольная матрица,

- нижнетреугольная матрица.

Симметричной называется квадратная матрица, у которой все элементы симметричны относительно главной диагонали.

Действия над матрицами

1. Суммой двух матриц иодного порядка называется матрица, каждый элемент которой равен сумме соответствующих элементов матриц А и В.

Из определения следует, что выполняются операции коммутативности сложения А+В=В+А и ассоциативности сложения А+(В+С)=(А+В)+С.

2. При умножении матрицы на числоk каждый ее элемент умножается на это число.

Отсюда следует, что общий множитель всех элементов матрицы можно вынести за знак матрицы.

Операция умножения матрицы на число обладает свойствами:

(α+β)А=αА+β;

α (А+В)= αА+ αВ,

где α и β – числа.

3. Умножение матриц. Пусть заданы матрицы и.

Произведением А×В называется матрица С порядка m×k:

А·В=·=С=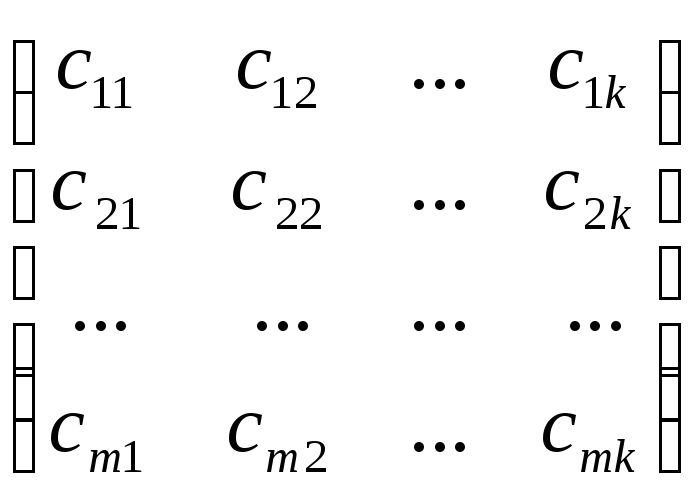

элементы которой вычисляются по формулам:

;

и т.д.

Операция перемножения матриц не коммутативна, то есть АВ≠ВА.

4. Транспонирование матрицы - это операция, при которой строки матрицы становятся столбцами, и наоборот.

Пример. Найти матрицу С=В(3А-2В), где А=и В=.

Решение. 1) Найдем матрицу (3А-2В)= 3- 2=-=.

2) С=В(3А-2В) = =.

Элементарные преобразования. Приведение матрицы к ступенчатому виду

1) можно менять строки (столбцы) местами;

2) можно умножать элементы строки на одно и то же число, отличное от нуля;

3) можно складывать (вычитать) строки друг с другом.

Верхнетреугольная матрица, у которой под главной диагональю все элементы равны нулю, называется приведенной к ступенчатому виду. При этом элементы, стоящие на главной диагонали называются угловыми элементами.

Ранг матрицы А – это максимальное число линейно независимых строк этой матрицы.

Утверждение. В ступенчатой матрице строки, содержащие ненулевые угловые элементы, линейно независимы. Отсюда следует, что ранг ступенчатой матрицы равен числу ее угловых элементов.

Приведение матрицы к ступенчатому виду с помощью метода Гаусса

Рассмотрим этот метод на примере матрицы А=

Поменяем вторую и первую строки местами (для ручного счета удобно, чтобы элемент был равен 1 или -1 (если это возможно)).

Получим матрицу

В дальнейшем первую строку менять не будем. Теперь с помощью элемента =-1 образуем нули в первом столбце, во второй, третьей и четвертой строках. Для этого ко второй строке прибавим первую, умноженную на число 2, из третьей строки вычтем первую, к четвертой прибавим первую строку:

Поменяем местами в этой матрице вторую и третью строки, и в дальнейшем первая и вторая строки меняться не будут. И с помощью элемента 1 получим нули во втором столбце в третьей и четвертой строках:

Здесь из третьей строки вычли вторую, умноженную на 5, а из четвертой – вторую, умноженную на 6.

Из четвертой строки вычтем третью, получим матрицу:

Угловые элементы -1, 1, 1, их число равно 3. следовательно, ранг матрицы равен 3.

Справедливы следующие теоремы.

Теорема 1. Элементарные преобразования не меняют ранга матрицы.

Теорема 2. Любую прямоугольную матрицу с помощью элементарных преобразований можно привести к ступенчатому виду.