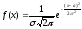Определенный интеграл
Интегральная сумма
∑f(ki)Δxi ( от i=1 до n )
где ki — произвольная точка соответствующего отрезка. Определенный интеграл функции f(x) на отрезке [а, b]
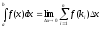
Формула Ньютона — Лейбница
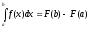
где F′ — первообразная функцию f(x), т е
F′(x)=f(x)
Некоторые свойства определенного интеграла
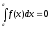
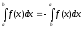

Площадь криволинейной трапеции, ограниченной графиком функции f(x), осью абсцисс и прямыми х=а и х=b,
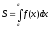
Площадь фигуры, ограниченной двумя кривыми y=.f1(x) и у = = f2(x) [ f'2(x)≥f1(x)] и двумя прямыми х=а и х=b,
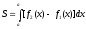
Дифференциальные уравнения
Общий вид дифференциального уравнения
F(x ,y,y′,y″,…yn) = О
Общee решение дифференциального уравнения
y=f(x, C1,C2, , Сn)
Общий вид дифференциального уравнения первого порядка
F(x,y,y') = 0
Общее решение дифференциального уравнения первого порядка
y= f(x,C)
примеры
1 Дифференциальное уравнение типа y'=f(x)
dy/dx=f(х) , dx = f(x)dx
Общее решение
y=∫f(x)dx=F(x)+C
-
Дифференциальное уравнение типа у' = f(y)
dy/dx=f(y), dy/f(y)=dx
Общее решение
∫dy/f(y)=F(y)+C
Дифференциальное уравнение с разделенными переменными
f(x) dx + φ(y)dy = 0
Общее решение
∫f(x) dx + ∫φ(y)dy = C, F(х) + Ф(у) = С
Дифференциальное уравнение с разделяющимися переменными
f(x)φ(y)dx+ψ(x)Ф(y)dy=0
Приведем это уравнение к уравнению с разделенными переменными
(f(x)/ψ(x))dx+(Ф(y)/φ(y))dy=0
Общее решение
∫(f(x)/ψ(x))dx+∫(Ф(y)/φ(y))dy=C, F1(x)+F2(y)=C
Теория вероятностей. Математическая статистика
Относительная частота события P*(A)=m/n
где п — число независимых испытаний, в которых случайное событие А происходит m раз.
Вероятность случайного события
P(A)=lim(m/n) (при n→∞)
Вероятность появления одного (безразлично какого) из нескольких несовместных событий (теорема сложения вероятностей). Для двух событий
P( А и В) = Р(А) + Р(В).
Вероятность совместного появления независимых событий (теорема умножения вероятностей) Для двух событий
P(А и В) = Р(А)Р(В].
вероятность того, что событие А произойдет l раз при п испы-таниях (биномиальное распределение)
Pin=n(n-1)•••(n_-l+1)Pl(1-P)n-1 ⁄ l!,
где Р — вероятность наступления события А.
Распределением дискретной случайной величины называют сово-
купность ее значений: х1, х2, ... и соответствующих вероятностей:
p(x1)=p1, p(x2)=p2 ….
Условие нормировки для дискретной случайной величины, имеющей п значений,
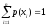
Среднее значение дискретной случайной величины
‹X›=(m1 x1+m2x2+…+mnxn)/n=x1m1/n+..+xnmn/n
где тi, — число дискретных случайных величин, имеющих значе-
ние xi.
Математическое ожидание дискретной случайной величины
M(X)= x1p1 +..+xnpn
Дисперсия дискретной случайной величины
D(X) = M{[X-M(X)]2},
D(X) = M(X2)-[M(X)]2,
Среднее квадратическое отклонение
Σ(X)=(D(X))1/2
Вероятность того, что непрерывная случайная величина принимает какое-либо значение в интервале (а, b)
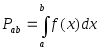
где f(x) — плотность вероятности (функция распределения вероятностей) .
Условие нормировки для непрерывной случайной величины
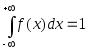
Функция распределения случайной величины

Математическое ожидание непрерывной случайной величины
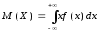
Дисперсия непрерывной случайной величины
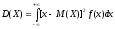
|
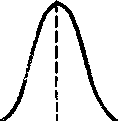
Нормальный закон распределения (закон Гаусса)
|
|
|
где а — математическое ожидание случайной величины, σ - среднее квадратическое отклонение. График закона распределения представлен на рис.
|
|
Функция распределения по нормальному закону
F(x)=Ф((x-a)/σ)
Значения функции Ф даны в табл
Плотность вероятности для проекции скорости молекул газа
на ось Ох
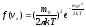
где то — масса молекулы, Т — термодинамическая температура газа, k — постоянная Больцмана.
Плотность вероятности для модуля скорости молекул газа (распределение Максвелла по скоростям)
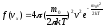
Средняя, средняя квадратичная и навероятнейшая скорости молекул

где R — молярная газовая постоянная, М — молярная масса Плотность вероятности нахождения молекулы газа в однородном гравитационном поле (пример распределения Больцмана)
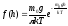
Давление газа (воздуха), находящегося в однородном гравитационном поле, на высоте h (барометрическая формула)
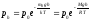
где рh— давление на высоте h=0
Концентрация молекул газа (воздуха), находящегося в однородном гравитационном поле, на высоте h
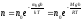
где nо — концентрация молекул газа на высоте h = О
Интервальная оценка генеральной средней (среднее значение генеральной совокупности)
‹ xв› - ε< μ < ‹ xв› + ε,
где ‹ xв› — выборочная средняя Эти неравенства выполняются с доверительной вероятностью Р Положительное число ε характеризует точность оценки и называется доверительным интервалом
При большой выборке (n>30)
τ=(εn0,5)/σ
где σ — генеральное среднее квадратическое отклонение Обычно в расчетах берется выборочное среднее квадратическое отклонение
Связь между τ и P
Ф(τ)=(1+P)/2
Значения функции Ф даны в табл
Значение функции Ф (t) для решения задач на нормальный закон распределения
|
t |
Ф(t) |
t |
Ф(t) |
t |
Ф(t) |
t |
Ф(t) |
|
0,0 |
0,5000 |
1,0 |
0,8413 |
2,1 |
0,9821 |
3,1 |
0,9990 |
|
0,1 |
0,5398 |
1,1 |
0,8643 |
2,2 |
0,9861 |
3,2 |
0,9993 |
|
0,2 |
0,5793 |
1,2 |
0,8840 |
2,3 |
0,9893 |
3,3 |
0,9995 |
|
0,3 |
0,6179 |
1,3 |
0,9032 |
2,4 |
0,9918 |
3,4 |
0,9997 |
|
0,4 |
0,6554 |
1,4 |
0,9192 |
2,5 |
0,9938 |
3,5 |
0,9998 |
|
0,5 |
0,6915 |
1,5 |
0,9332 |
2,6 |
0,9953 |
3,6 |
0,9998 |
|
0,6 |
0,7257 |
1,6 |
0,9452 |
2,7 |
0,9965 |
3,7 |
0,9999 |
|
0,7 |
0,7580 |
1,7 |
0,9554 |
2,8 |
0,9974 |
3,8 |
0,9999 |
|
0,8 |
0,7881 |
1,8 |
0,9641 |
2,9 |
0,9981 |
3,9 |
1,000 |
|
0,9 |
0,8159 |
1,9 |
0,9713 |
3,0 |
0,9986 |
|
|
|
|
|
2,0 |
0,9772 |
|
|
|
|
Интервальная оценка генеральной средней при малой выборке
n≤30
ε=ts/n0,5
Здесь s2=nσb2/(n-1)— исправленная выборочная дисперсия,
где σb2 — выборочная дисперсия Параметр t (коэффициент Стьюдента) для заданных п и Р находят по табл.
Коэффициент Стьюдента
|
п |
Р |
||||||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
0,999 |
|
|
2 |
0,16 |
0,33 |
0,51 |
0,73 |
1,00 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
31,8 |
63,7 |
636,6 |
|
3 |
14 |
29 |
45 |
62 |
0,82 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
31,6 |
|
4 |
14 |
28 |
42 |
58 |
77 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,5 |
5,8 |
12,9 |
|
5 |
13 |
27 |
41 |
57 |
74 |
94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
8,6 |
|
6 |
13 |
27 |
41 |
56 |
73 |
92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
6,9 |
|
7 |
13 |
27 |
40 |
55 |
72 |
90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
3,7 |
6,0 |
|
8 |
13 |
26 |
40 |
55 |
71 |
90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
3,5 |
5,0 |
|
9 |
13 |
26 |
40 |
54 |
71 |
90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
3,4 |
5,0 |
|
10 |
13 |
26 |
40 |
54 |
70 |
88 |
1,1 |
1,4 |
1,9 |
2,3 |
2,8 |
3,3 |
4,8 |
|
11 |
13 |
26 |
40 |
54 |
70 |
88 |
1,1 |
1,4 |
1,8 |
2,2 |
2,8 |
3,2 |
4,6 |
|
12 |
13 |
26 |
40 |
54 |
70 |
87 |
1,1 |
1,4 |
1,8 |
2,2 |
2,7 |
3,1 |
4,5 |
|
13 |
13 |
26 |
40 |
54 |
70 |
87 |
1,1 |
1,4 |
1,8 |
2,2 |
2,7 |
3,1 |
4,3 |
|
14 |
13 |
26 |
39 |
54 |
69 |
87 |
1,1 |
1,4 |
1,8 |
2,2 |
2,7 |
3,0 |
4,2 |
|
15 |
13 |
26 |
39 |
54 |
69 |
87 |
1,1 |
1,3 |
1,8 |
2,1 |
2,6 |
3,0 |
4,1 |
|
16 |
13 |
26 |
39 |
54 |
69 |
87 |
1,1 |
1,3 |
1,8 |
2,1 |
2,6 |
2,9 |
4,0 |
|
17 |
13 |
26 |
39 |
54 |
69 |
86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,6 |
2,9 |
4,0 |
|
18 |
13 |
26 |
39 |
53 |
69 |
86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,6 |
2,9 |
4,0 |
|
19 |
13 |
26 |
39 |
53 |
69 |
86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,6 |
2,9 |
3,9 |
|
20 |
13 |
26 |
39 |
53 |
69 |
86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,5 |
2,9 |
3,9 |
|
21 |
13 |
26 |
39 |
53 |
69 |
86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,5 |
2,8 |
3,8 |
|
22 |
13 |
26 |
39 |
53 |
69 |
86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,5 |
2,8 |
3,8 |
|
23 |
13 |
26 |
39 |
53 |
69 |
86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,5 |
2,8 |
3,8 |
|
24 |
13 |
26 |
39 |
53 |
69 |
86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,5 |
2,8 |
3,8 |
|
25 |
13 |
26 |
39 |
53 |
69 |
86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,5 |
2,8 |
3,7 |
|
26 |
13 |
26 |
39 |
53 |
68 |
86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,5 |
2,8 |
3,7 |
|
27 |
13 |
26 |
39 |
53 |
68 |
86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,5 |
2,8 |
3,7 |
|
28 |
13 |
26 |
39 |
53 |
68 |
86 |
1,1 |
1,3 |
1,7 |
2,0 |
2,5 |
2,8 |
3,7 |
|
29 |
13 |
26 |
39 |
53 |
68 |
86 |
1,1 |
1,3 |
1,7 |
2,0 |
2,5 |
2,8 |
3,7 |
|
30 |
13 |
26 |
39 |
53 |
68 |
85 |
1,1 |
1,3 |
1,7 |
2,0 |
2,5 |
2,8 |
3,7 |
|
40 |
13 |
26 |
39 |
53 |
68 |
85 |
1,1 |
1,3 |
1,7 |
2,0 |
2,4 |
2,7 |
3,6 |
|
60 |
13 |
25 |
39 |
53 |
68 |
85 |
1,1 |
1,3 |
1,7 |
2,0 |
2,4 |
2,7 |
3,5 |
|
120 |
13 |
25 |
39 |
53 |
68 |
85 |
1,1 |
1,3 |
1,7 |
2,0 |
2,4 |
2,6 |
3,4 |
|
00 |
13 |
25 |
39 |
52 |
67 |
84 |
1,1 |
1,3 |
1,7 |
2,0 |
2,3 |
2,6 |
3,3 |