Дерево Штейнера с евклидовой метрикой

_{Огромный практический интерес представляет решение проблемы дерева Штейнера на плоскости. Для любых двух пар вершин графа u=(ux,uy) и v=(vx,vy), заданных координатами на плоскости, расстояние задается в Lp-метрике (1 p ):}

||uv||_p=(|u_x–v_x|^p+ |u_y–u_y|^p)^1/p.

Для двух специальных случаев:

• Евклидово расстояние ||uv||₂=((u_x–v_x)²+ (u_y–u_y)²)^1/2;

• Прямоугольное расстояние ||uv||₁=|u_x–v_x| + |u_y–u_y|.

Алгоритм построения дерева Штейнера с евклидовой метрикой

На плоскости задано Nточек, изF- терминальные.

Алгоритм приблизительного построения дерева Штейнера:

1. Построить полносвязный граф G’=(N,E’) на вершинахN. Расстоянием между двумя вершинами этого графа будет кратчайшее расстояние между этими вершинами. Взять эти расстояния в качестве весов.

2. Найти минимальное каркасное дерево Т’ полносвязного графа G’.

3. Подставить минимальное каркасное дерево T’ в исходный графG. Заменить каждое ребро дереваT’ минимальным путем исходного графаG. В результате получится новый графT’’ (не всегдаT’’ будет деревом).

4. Найти каркасное дерево графа T’’, которое будет приблизительным деревом Штейнера.

Аппроксимационное отношение этого алгоритма равно 2.

Пример

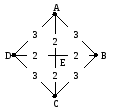
G=(V,E)

N={A,B,C,D}

G’=(N,E’)

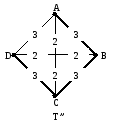
Рис.3.4.4. Построение дерева Штейнера (выделено жирным)

Замечание

Е

Пример

сли допускается введение на плоскости дополнительных «искусственных» вершин (они становятся вершинами Штейнера), то вес минимального дерева Штейнера можно уменьшить соответствующим подбором вершин Штейнера.

Исходная задача

Дерево Штейнера

(длина=9)

Дерево Штейнера с дополнительными вершинами Штейнера

(длина=7)

Рис.3.4.5. Решение задачи Штейнера в прямоугольных координатах

4. Деревья Штейнера с ограничениями

   1. Д

      Определение

      ерево Штейнера с ограничением степеней

Задан простой связной ненаправленный G=(V,E)cnвершинами, неотрицательными весами реберc_ij, подмножеством терминальных вершинZVи ограничениями степеней вершинk_i2.

Проблемой Штейнера с ограничениями на степени вершин (TheDegree-constrainedSteinerProblem–DCSP) является нахождение на графе дерева Т такого, что степень каждой вершины дереваdeg(i)k_i, а сумма весов ребер этого дерева минимальна среди всех возможных деревьев с ограничениями на степени вершин.

Класс сложности

Класс сложности DCSP–NP-тяжелая.

Алгоритмы

Точные алгоритмы решения DCSP(алгоритм перечисления каркасных деревьев и динамический программный алгоритм) имеют сложностьO(p²2^(n-p)+n³) иO(n3^p+n²2^p+n) соответственно. Получить решения в приемлимое время для графа с десятком вершин проблематично.

Существует достаточно большое число эвристических алгоритмов, ряд из них дает расхождение решения на 10% от точного решения.

2. Д

   Определение

   ерево Штейнера с ограничением запаздывания

Задан простой связный ненаправленный граф G=(V,E) и две весовые функции на ребрах графа: функция стоимости с_ij и функция запаздыванияD_ij. Обе функции являются целыми положительными числами. Кроме того, задана вершина-истокsи терминальные вершиныSV.

Проблема нахождения дерева Штейнера с ограничением запаздывания:

Найти дерево Штейнера при условии, сумма запаздываний всех путей этого дерева от вершины sво все терминальные вершины не превышает некоторой положительной величины.

Класс сложности

Класс сложности данной проблемы – NP-тяжелый.

Алгоритмы

Имеется несколько эвристических алгоритмов решения данной проблемы.