
Роздивимося невизначені інтеграли виду де— раціональна функція віді.
Можливі такі випадки:
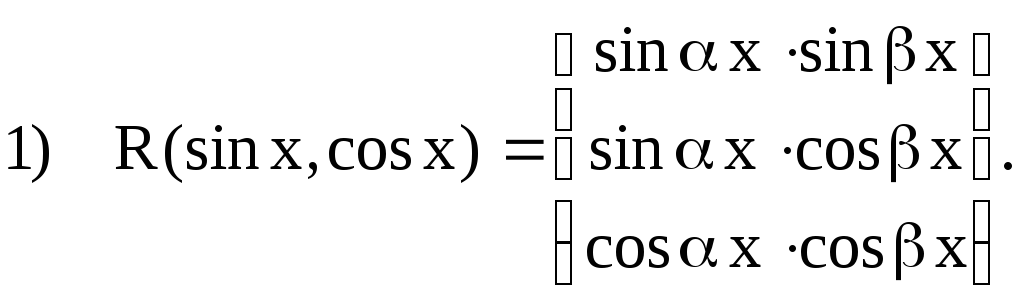
У даному випадку використовуються такі формули:
![]()
![]()
Приклад 1:

![]() (добуток парних
позитивних степенів синусів і косинусів).
(добуток парних
позитивних степенів синусів і косинусів).
У даному випадку використовуються формули:
![]()
Приклад 2:

3)
![]() підінтегральна
функція непарна відносно синуса. У цьому
випадку застосовується підстановка
підінтегральна
функція непарна відносно синуса. У цьому
випадку застосовується підстановка
![]()
Перед тим , як виконати заміну перемінної необхідно виконати наступне:
від непарного степеня
 відокремлити в якості співмножника
відокремлити в якості співмножника в
першому степені;
в
першому степені;парний степінь
 ,
який залишився , виразити через
,
який залишився , виразити через ,
використовуючи основну тригонометричну
тотожність
,
використовуючи основну тригонометричну
тотожність ;
;виконати заміну

Приклад 3:

підінтегральна
функція непарна відносно
![]() Використовується
заміна перемінних
Використовується
заміна перемінних![]() При цьому з непарним степенем
При цьому з непарним степенем![]() здійснюються перетворення, аналогічні
тим, що були зроблені з
здійснюються перетворення, аналогічні
тим, що були зроблені з![]() у попередньому випадку.
у попередньому випадку.
![]() підінтегральна
функція парна відносно
підінтегральна
функція парна відносно
![]() і
і![]() .
.
Здійснюємо заміну
![]() тоді
тоді![]()
Приклад 4:

Якщо підінтегральна функція не відповідає жодному з випадків 1) - 5), то використовуємо універсальну тригонометричну підстановку:
![]()
Приклад 5:

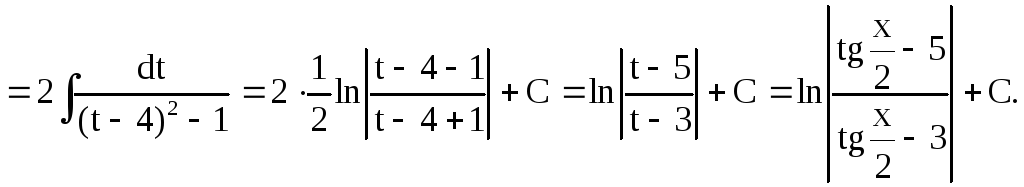
ІНТЕГРУВАННЯ ДЕЯКИХ ІРРАЦІОНАЛЬНИХ ВИРАЗІВ
![]() де
де
![]() - раціональна функція. У даному випадку
здійснюється замінаx
= tk
, де k-
найменше спільне кратне показників
коренів: k
= НСК{n,
r,
…}...
- раціональна функція. У даному випадку
здійснюється замінаx
= tk
, де k-
найменше спільне кратне показників
коренів: k
= НСК{n,
r,
…}...
Приклад 1:


Виконуємо
заміну:
![]() де
k- найменше
спільне
кратне
показників
коренів:
k = НСК{n,
r, …}...
де
k- найменше
спільне
кратне
показників
коренів:
k = НСК{n,
r, …}...
Приклад 2:
![]() Виконаємо заміну:
Виконаємо заміну:
![]()
Тоді маємо:
![]()



У даному випадку використовуються такі тригонометричні підстановки, які дозволяють позбутися ірраціональності в підінтегральній функції:

Приклад 3:
![]() Введемо заміну:
Введемо заміну:
![]()

![]() де
де
![]() - раціональна функція від зазначених
змінних.
- раціональна функція від зазначених
змінних.
Розглянемо окремі випадки:
4.1. ![]() У даному випадку необхідно:
У даному випадку необхідно:
винести a за знак радикала,
під радикалом виділити повний квадрат.
У результаті
приходимо до інтеграла
Зауваження. Слід зазначити, що для перебування інтегралів, які мають вигляд
![]() більш ефективним
є метод інтегрування по частках.
більш ефективним
є метод інтегрування по частках.
Приклад 4:
![]()
Знайдемо
 відкіля,
якщо перенести шуканий інтеграл у ліву
частину рівності, одержимо:
відкіля,
якщо перенести шуканий інтеграл у ліву
частину рівності, одержимо:
![]()
Остаточно
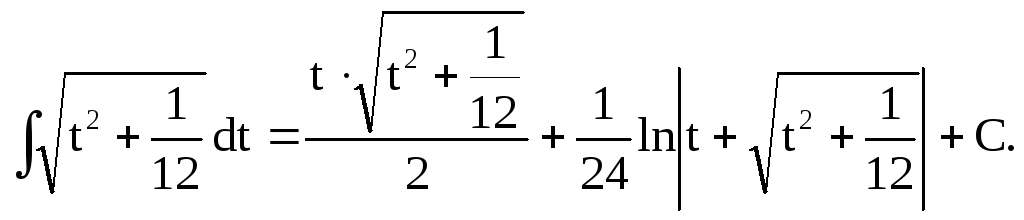
Відповідь:
![]()
![]()
4.2. ![]()
У даному випадку необхідно виконати такі дії:
винести коефіцієнт а за радикал,
виділити під радикалом повний квадрат.
У результаті приходимо до одного з інтегралів:
![]()
![]() .
.
4.3. ![]()
Тут необхідно:
у чисельнику виділити похідну від підкореневого виразу знаменника,
перейти до суми двох інтегралів (один - табличний:
 другий - інтеграл типу 4.2.).
другий - інтеграл типу 4.2.).
Приклад 5:


4.4. ![]() У цьому випадку підстановка типу
У цьому випадку підстановка типу![]() приводить до інтеграла типу 4.3.
приводить до інтеграла типу 4.3.
Варіанти індивідуальних завдань
Варіант 1
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
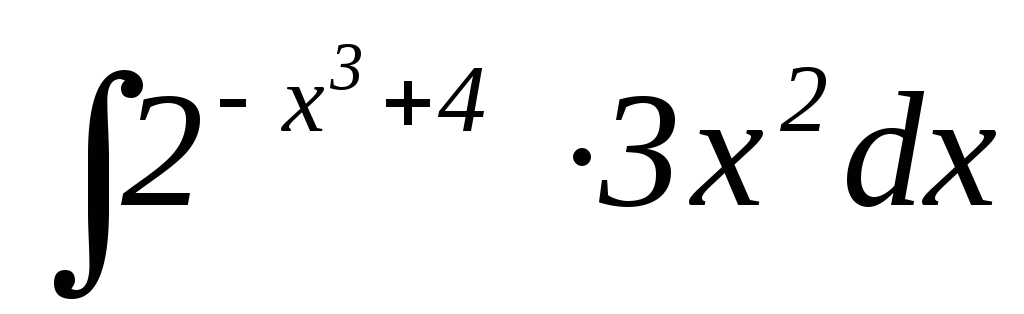 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 
Варіант 2
 15.
15. 
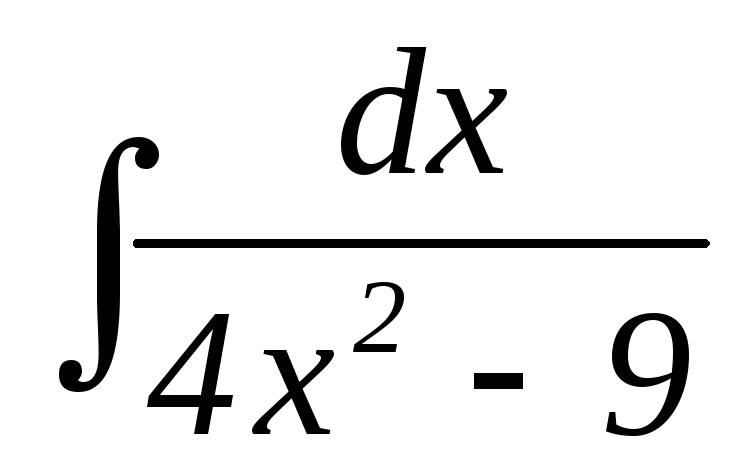 16.
16.

 17.
17.

 18.
18. 
 19.
19. 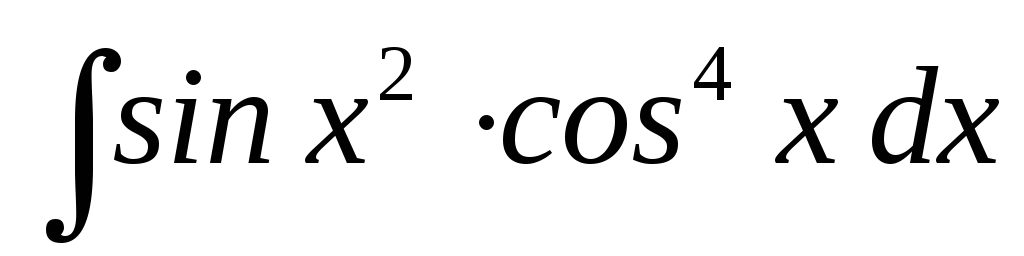
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 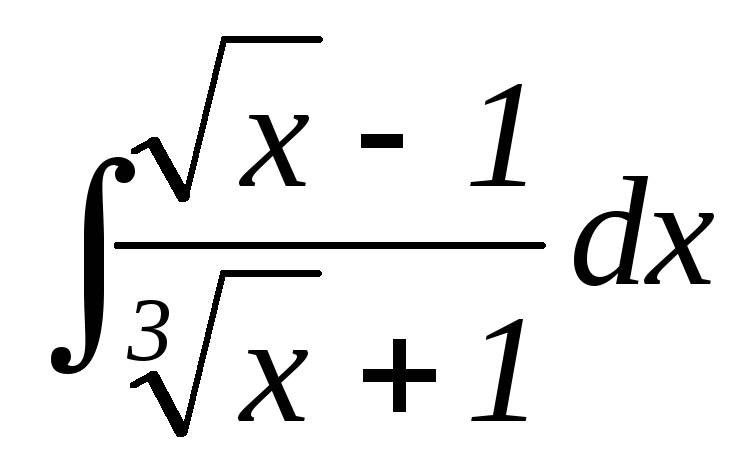
 26.
26. 
 27.
27. 
 28.
28. 
Варіант 3
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
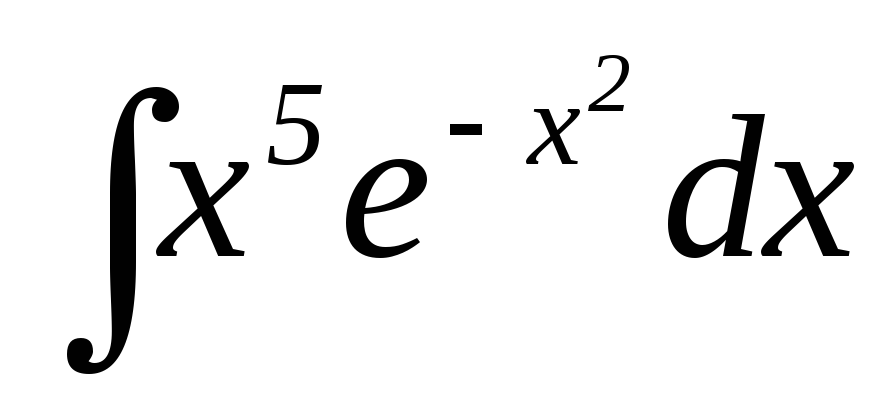 26.
26. 
 27.
27. 
 28.
28. 
Варіант 4
 15.
15. 
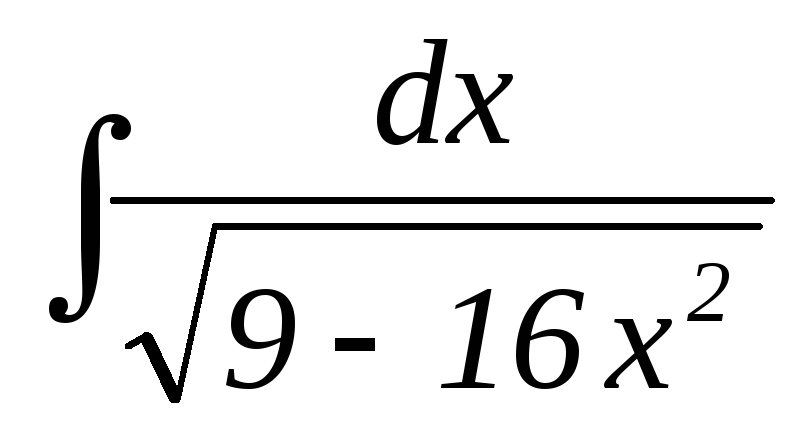 16.
16.
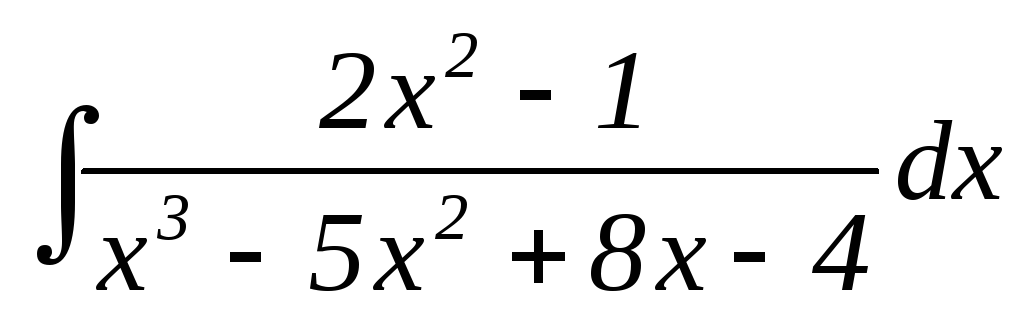
 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 
Варіант 5
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 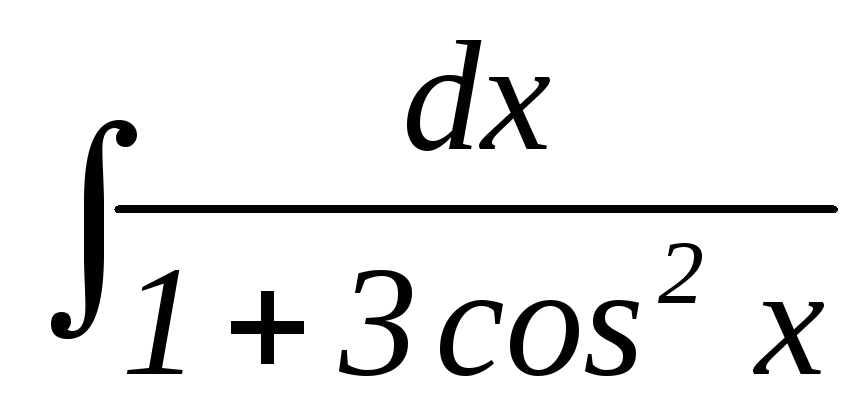
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 
Варіант 6
 15.
15. 
 16.
16.

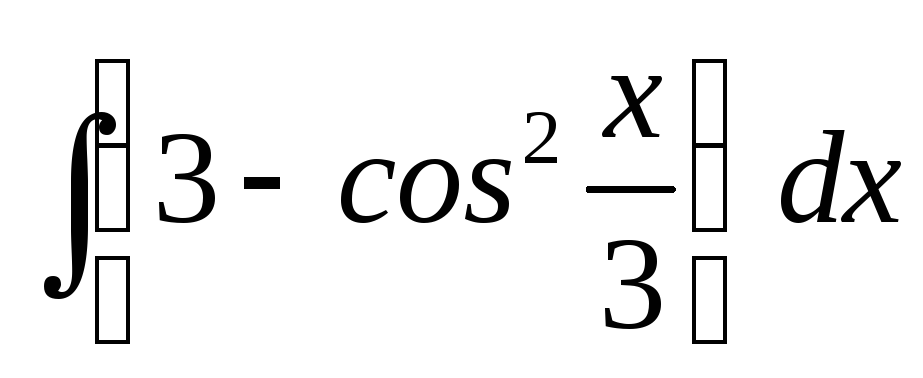 17.
17.

 18.
18. 
 19.
19. 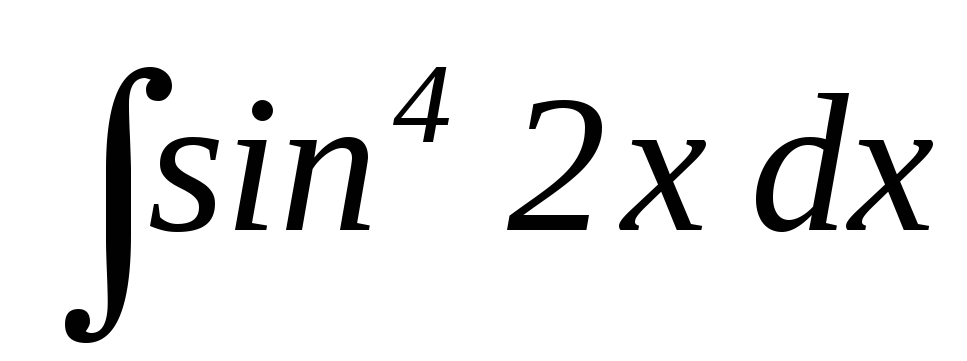
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 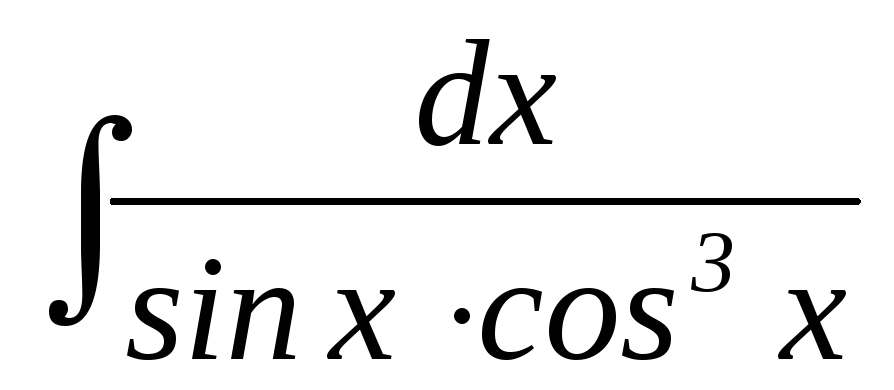
 25.
25. 
 26.
26. 
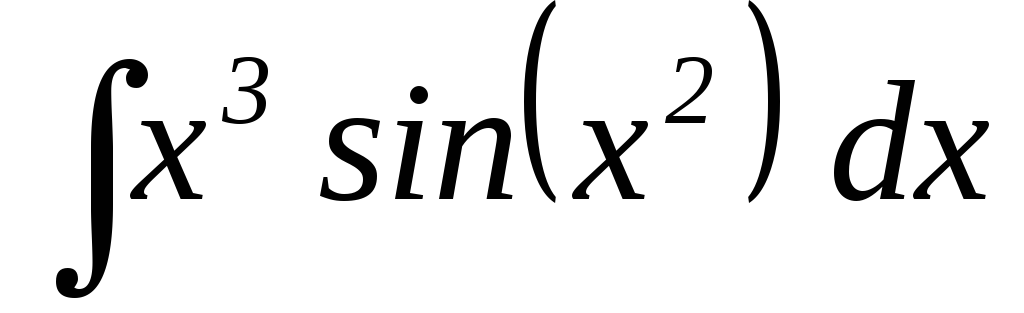 27.
27. 
 28.
28. 
Варіант 7
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 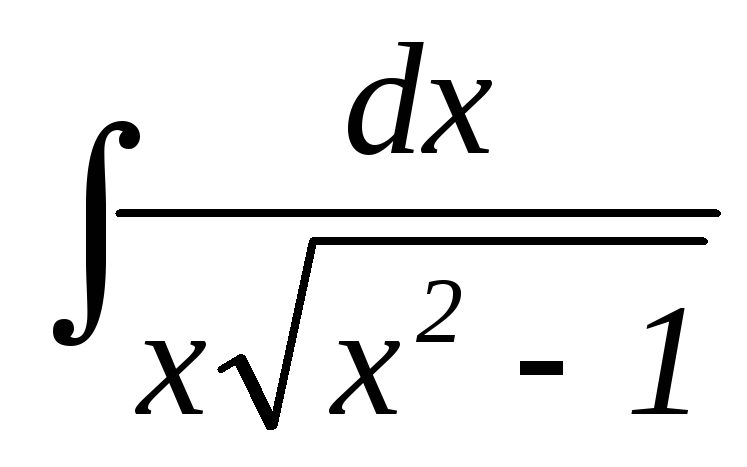
 28.
28. 
Варіант 8
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
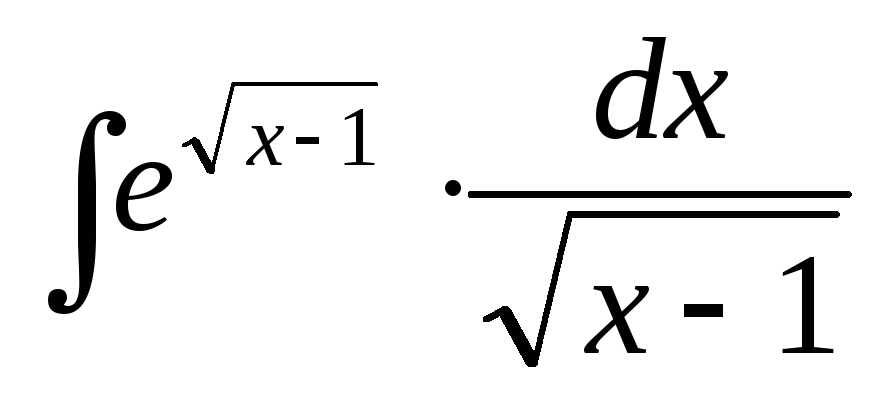 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 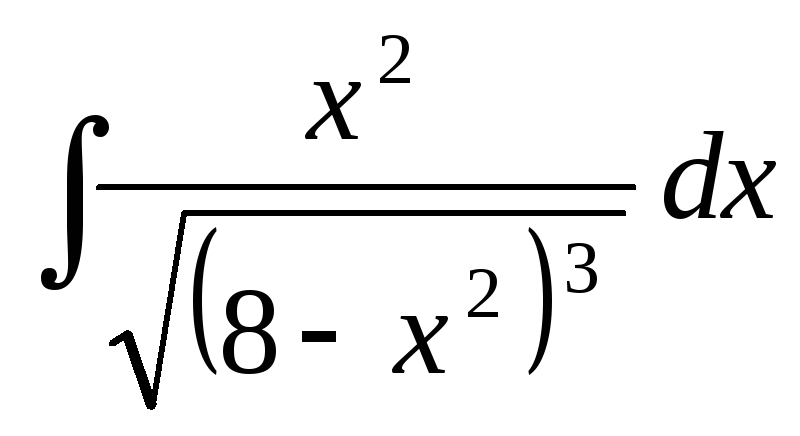
 27.
27. 
 28.
28. 
Варіант 9
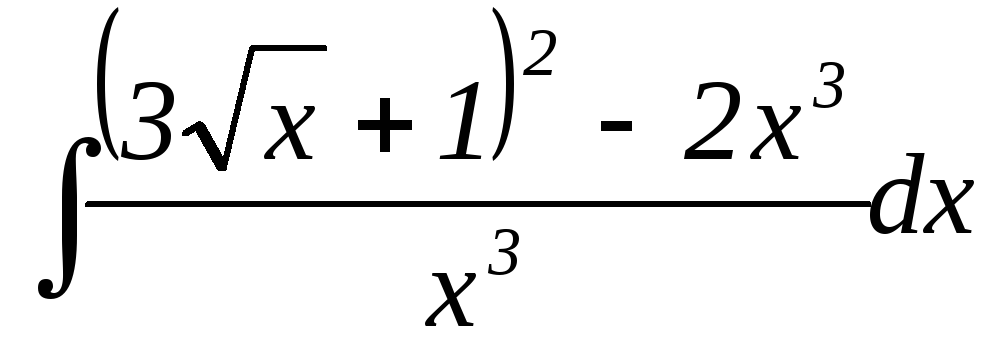 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 
Варіант 10
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
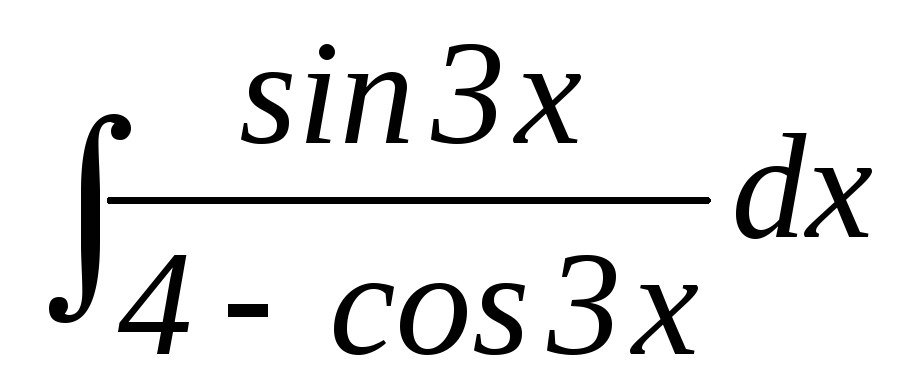 19.
19. 
 20.
20. 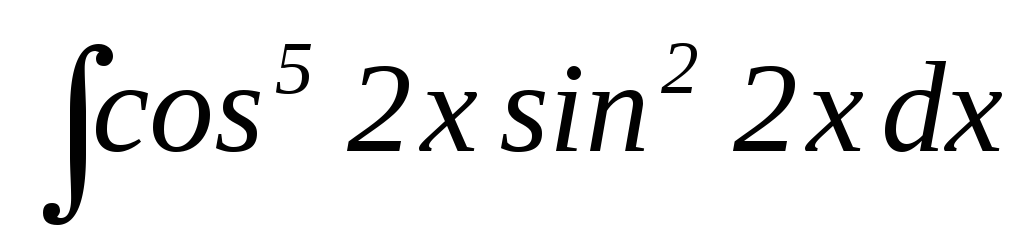
 21.
21. 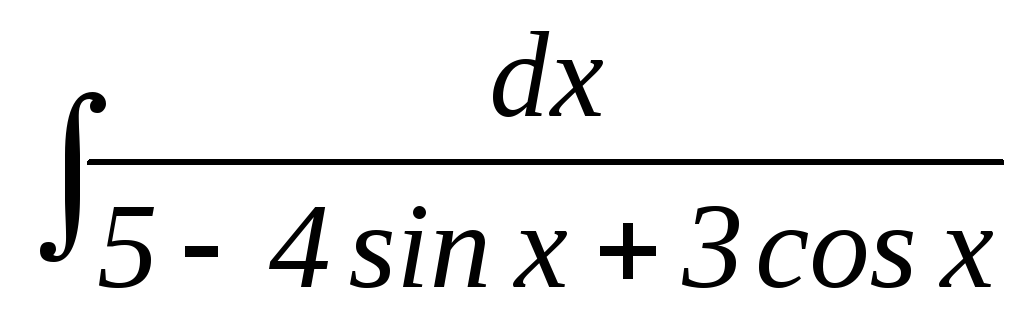
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 
Варіант 11
 15.
15. 
 16.
16.
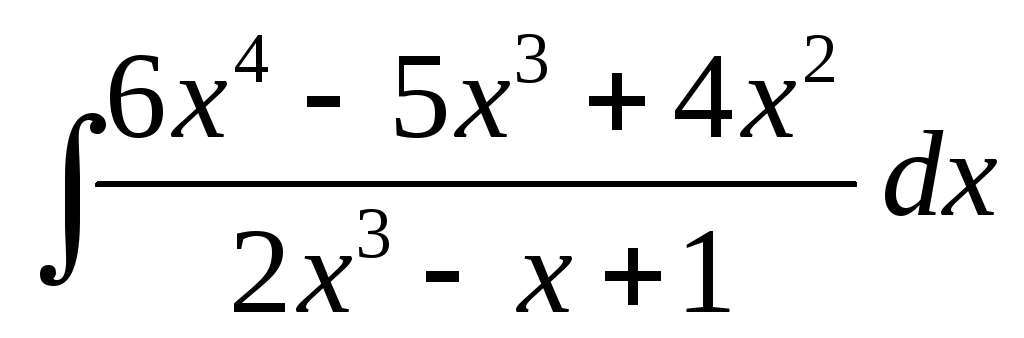
 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
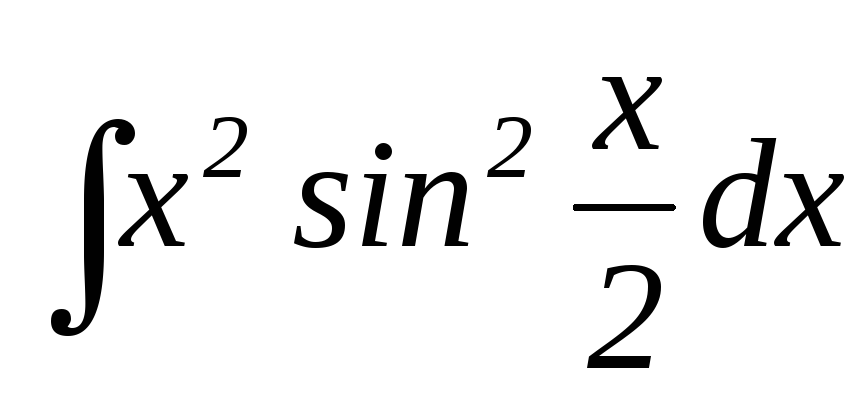 26.
26. 
 27.
27. 
 28.
28. 
Варіант 12
 15.
15. 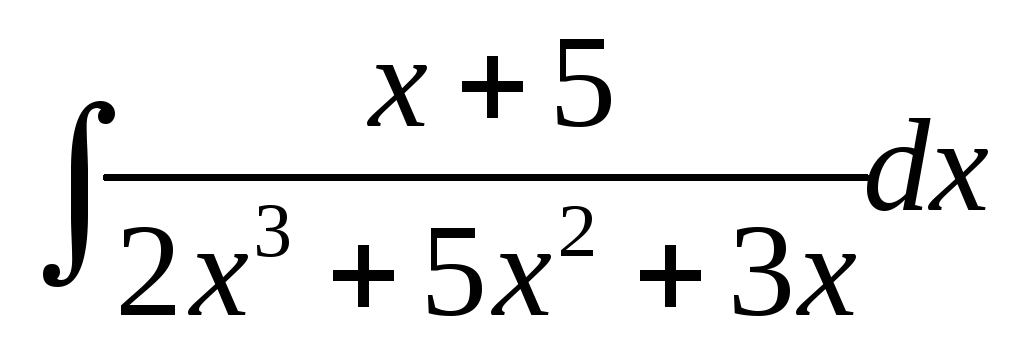
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
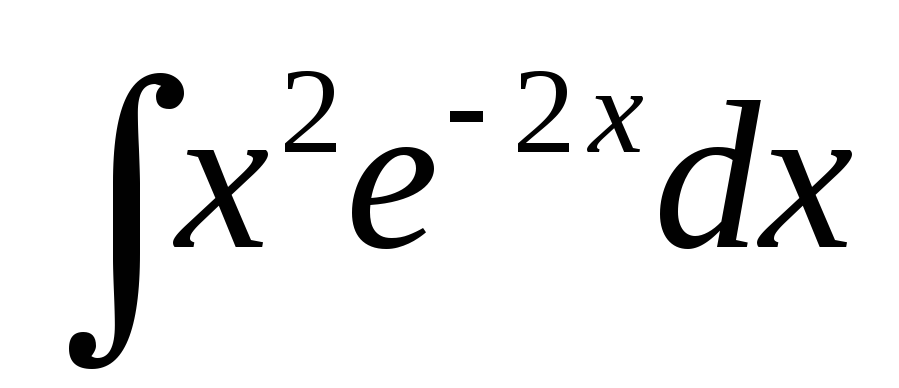 26.
26. 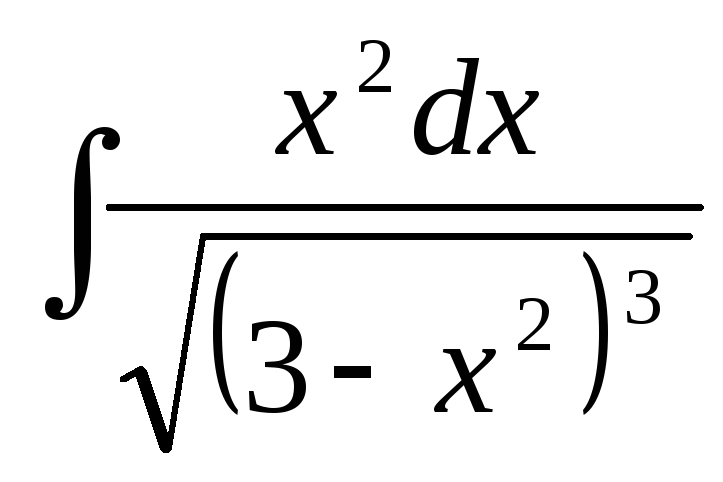
 27.
27. 
 28.
28. 
Варіант 13
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
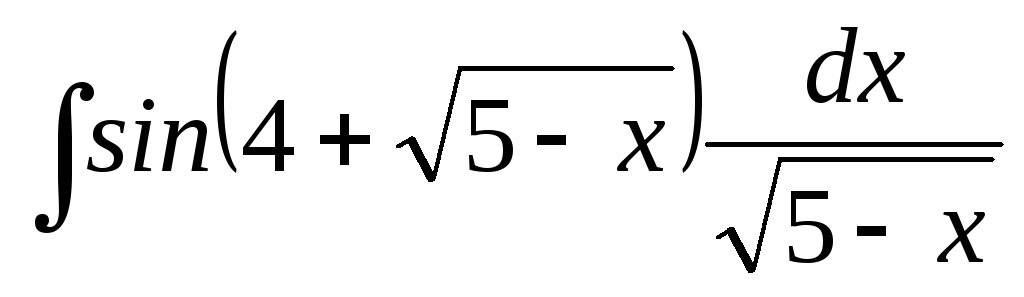 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
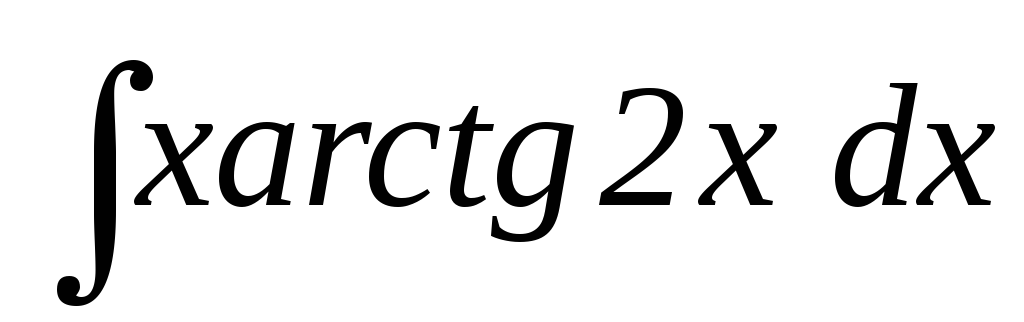 27.
27. 
 28.
28. 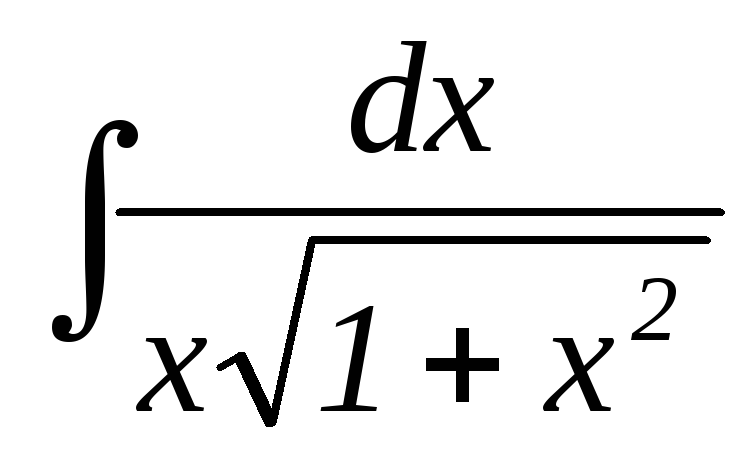
Варіант 14
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 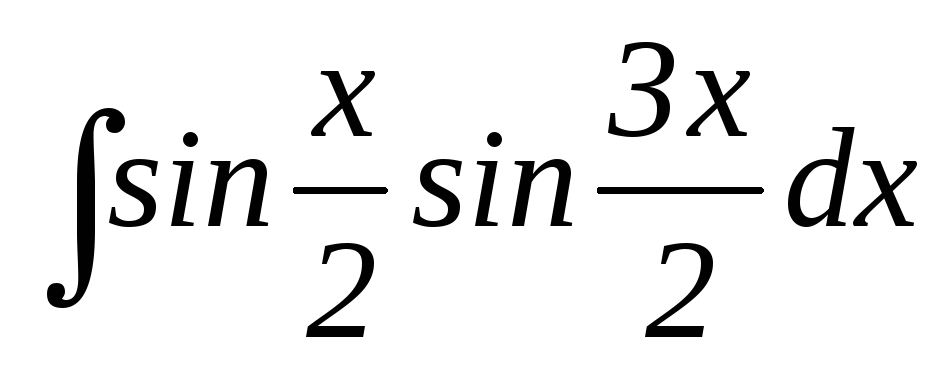
 19.
19. 
 20.
20. 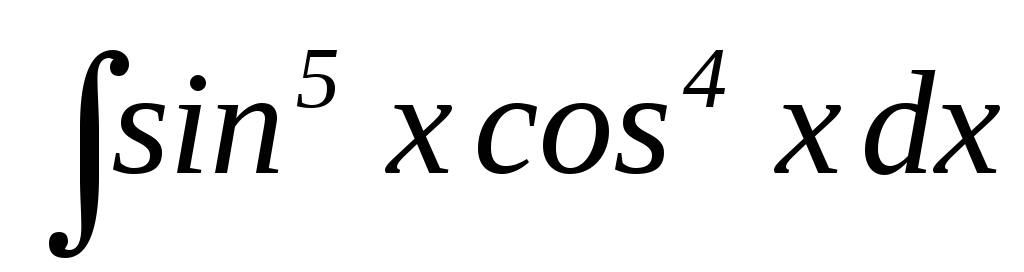
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
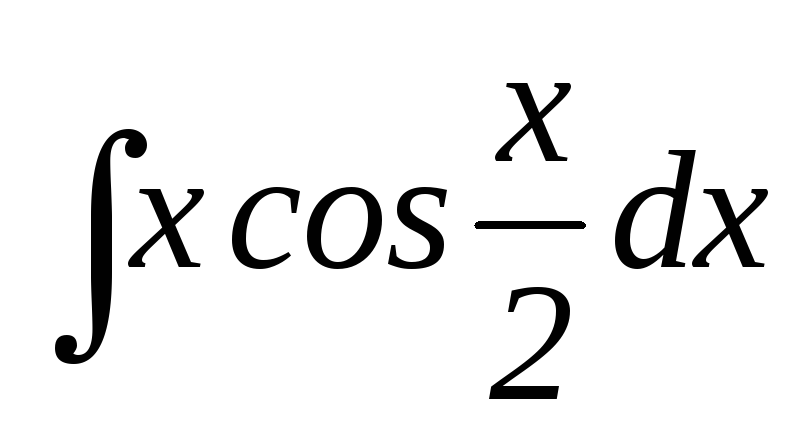 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 
Варіант 15
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
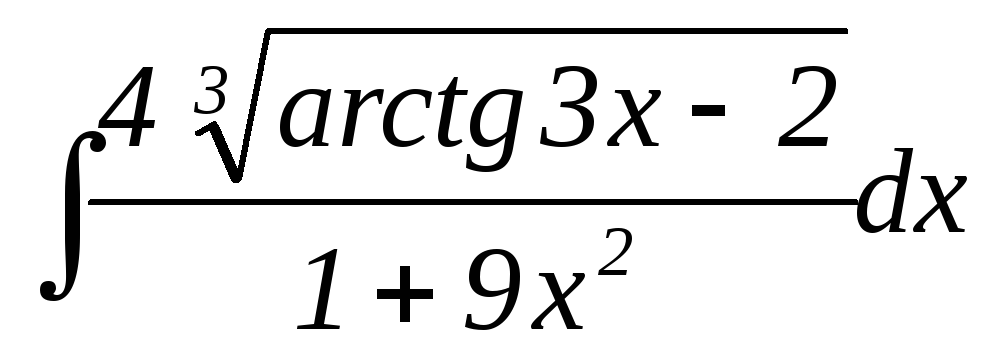 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
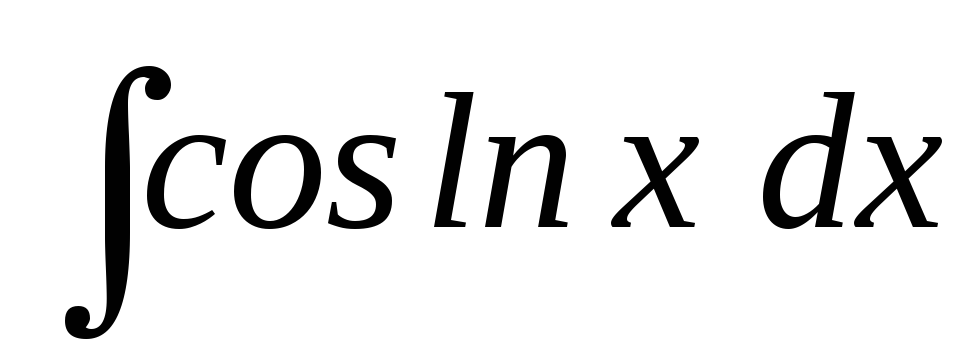 28.
28. 
Варіант 16
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 
Варіант 17
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
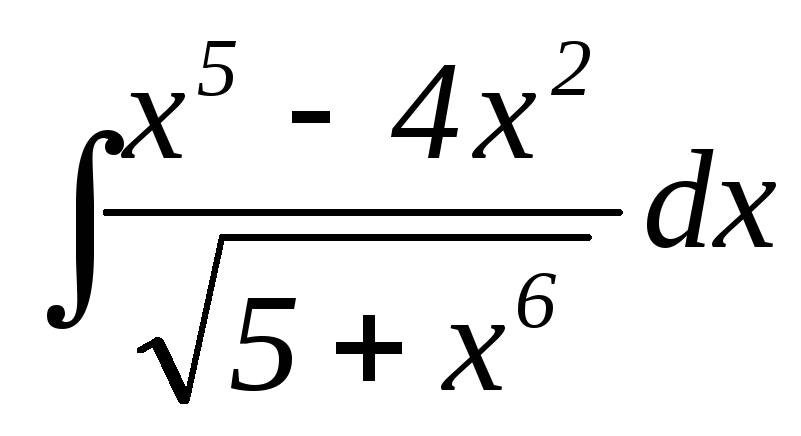 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
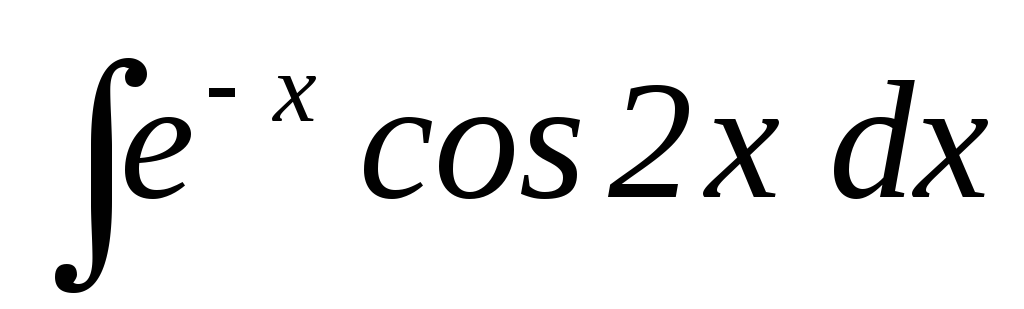 28.
28. 
Варіант 18
 15.
15. 
 16.
16.
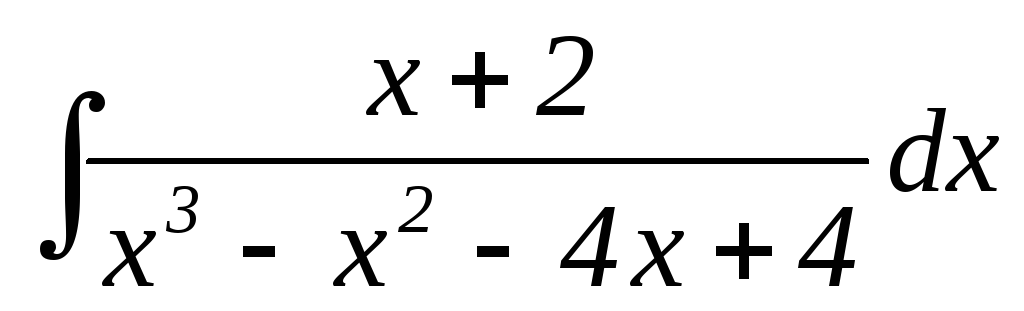
 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
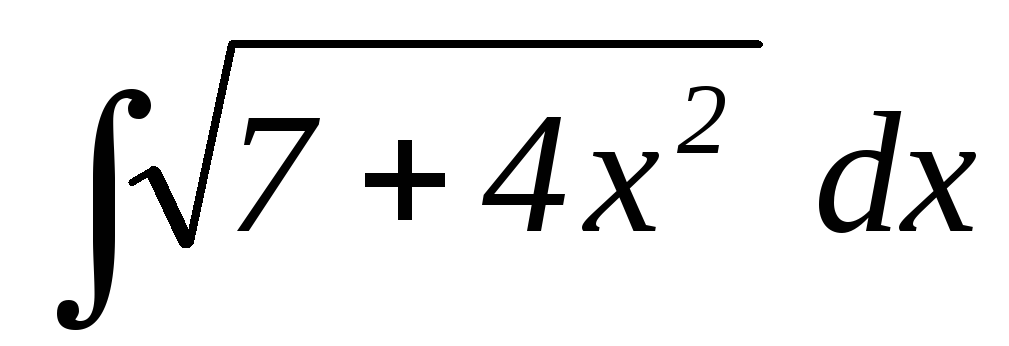 28.
28. 
Варіант 19
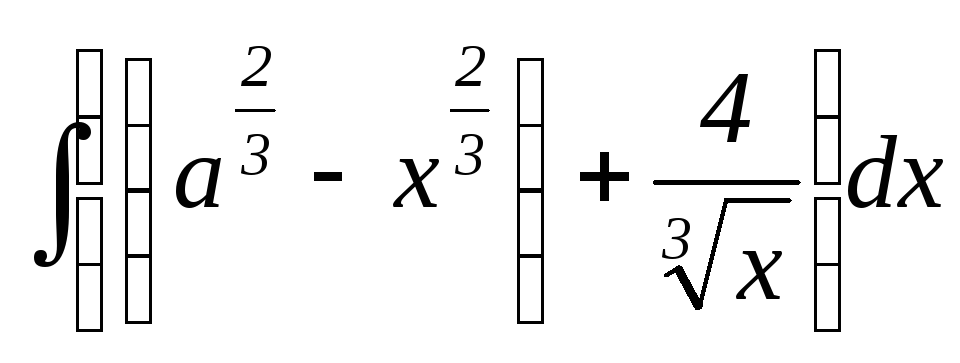 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
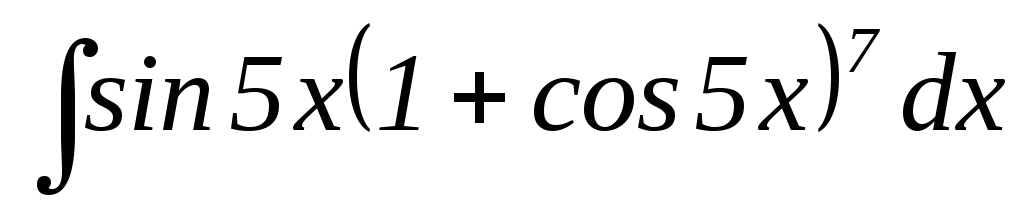 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
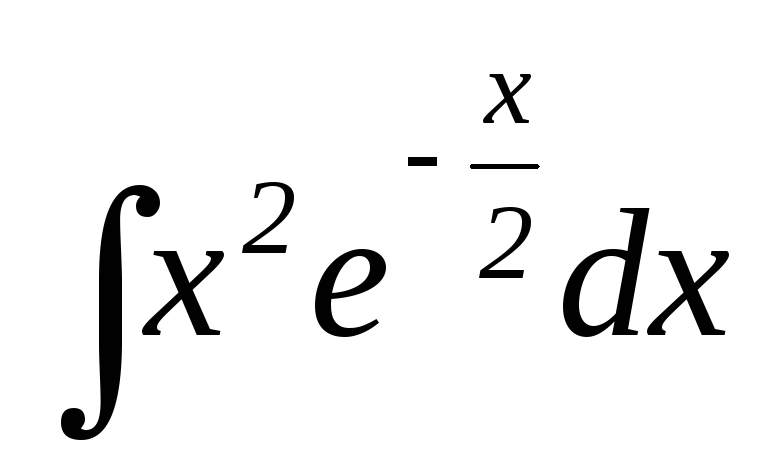 26.
26. 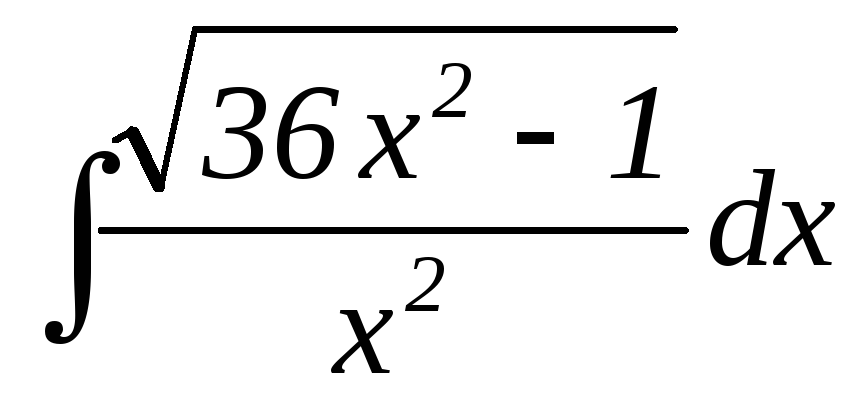
 27.
27. 
 28.
28. 
Варіант 20
 15.
15. 
 16.
16.

 17.
17.

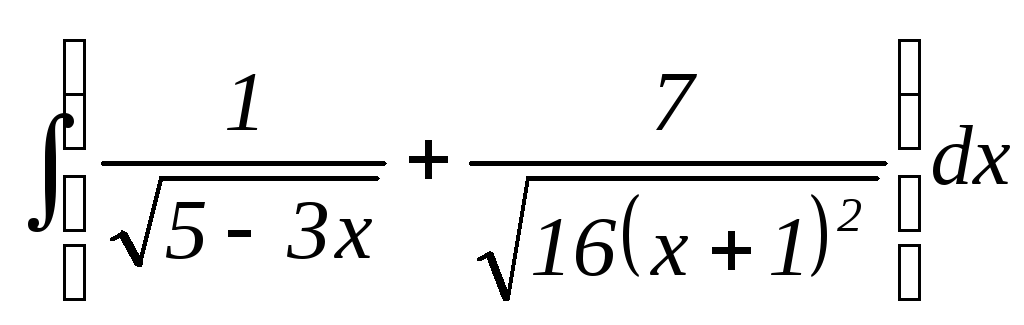 18.
18. 
 19.
19. 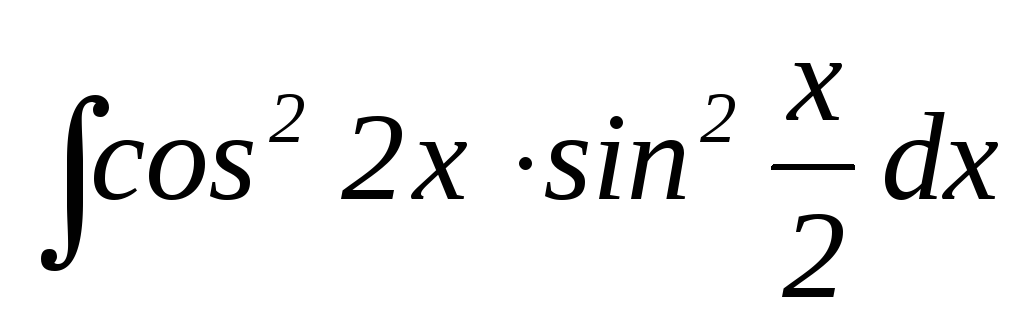
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
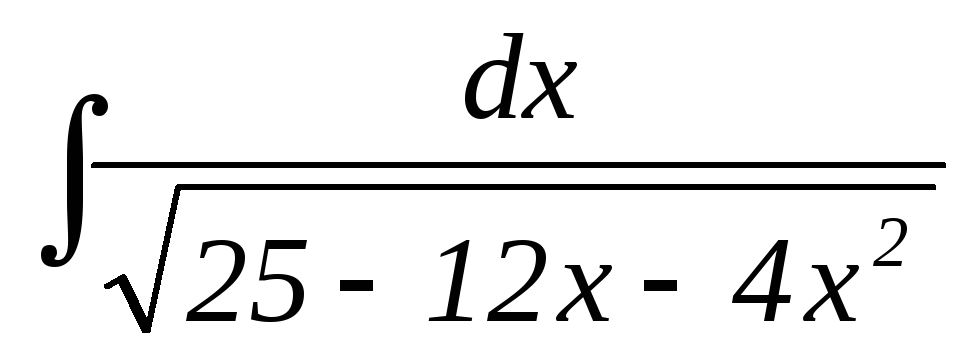 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 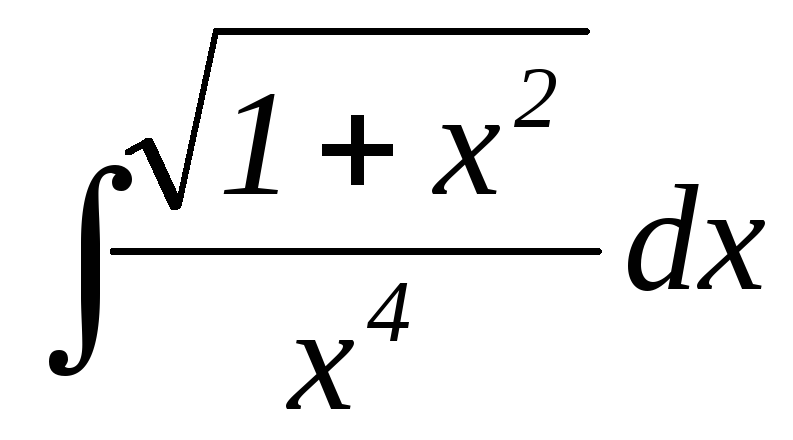
Варіант 21
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 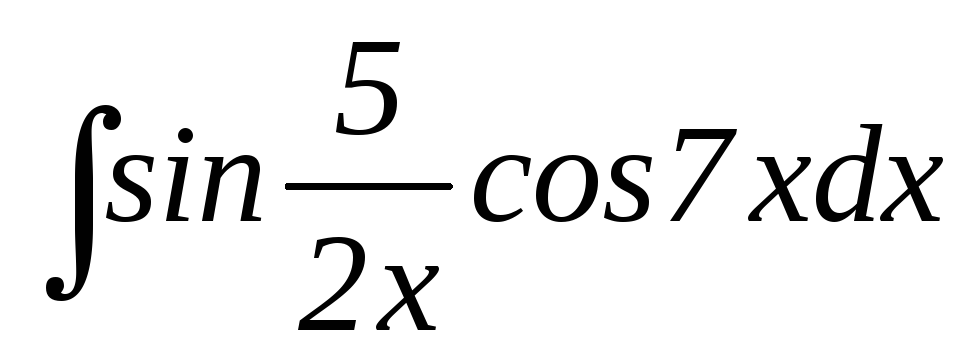
 19.
19. 
 20.
20. 
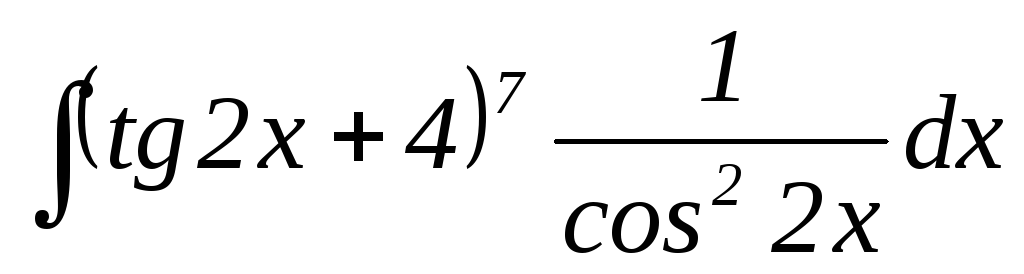 21.
21. 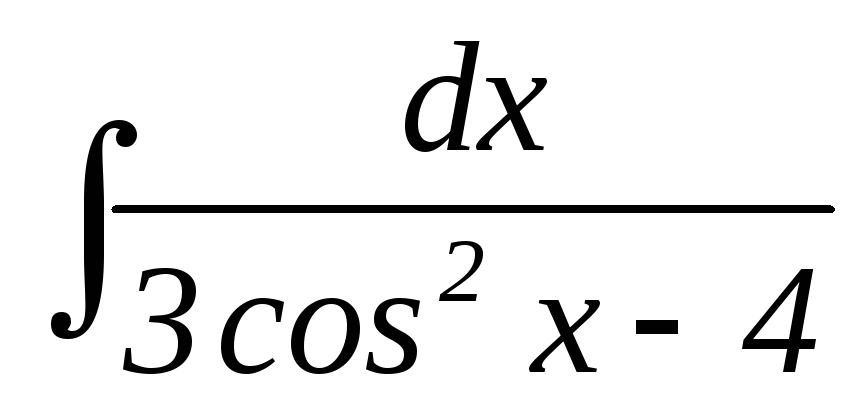
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 
Варіант 22
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 
Варіант 23
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 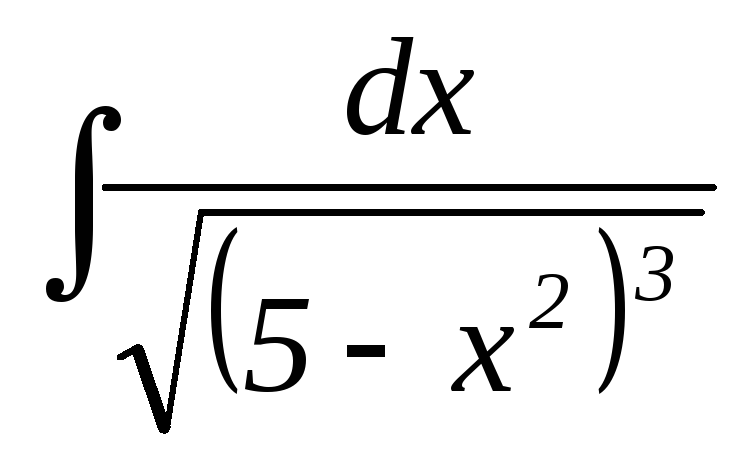
Варіант 24
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 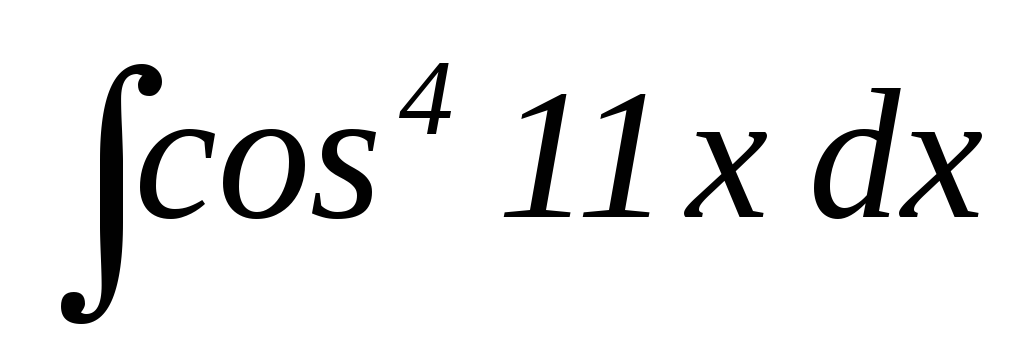
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 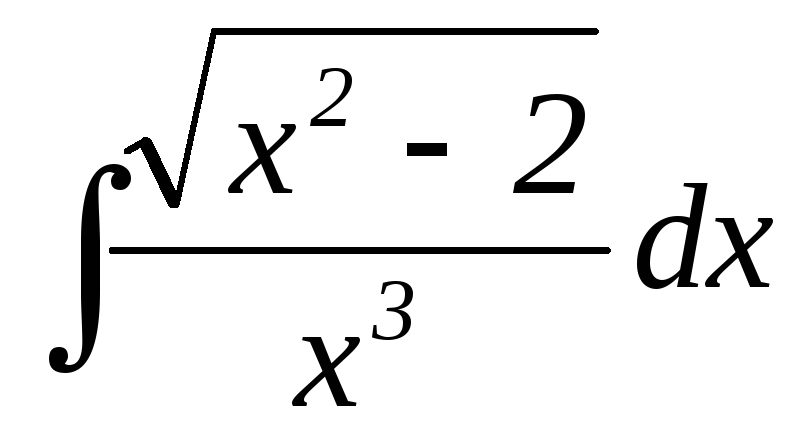
Варіант 25
 15.
15. 
 16.
16.

 17.
17.
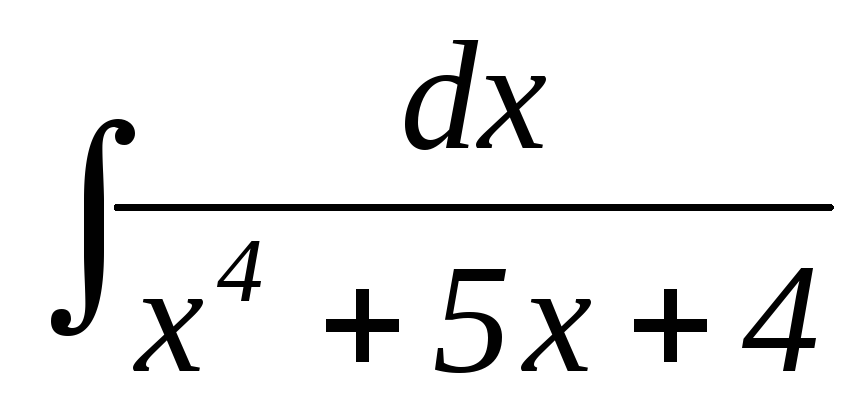
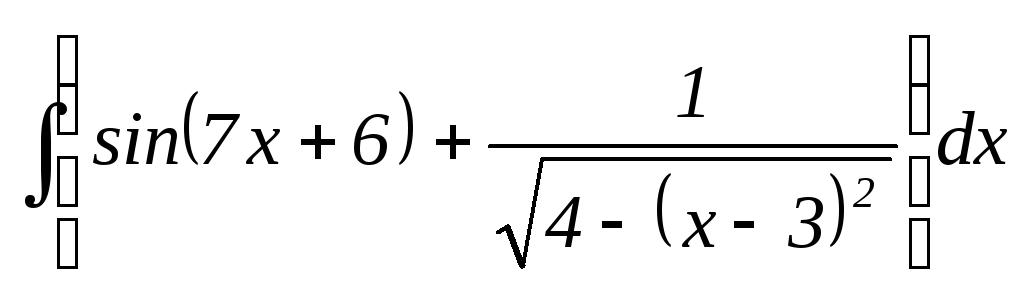 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
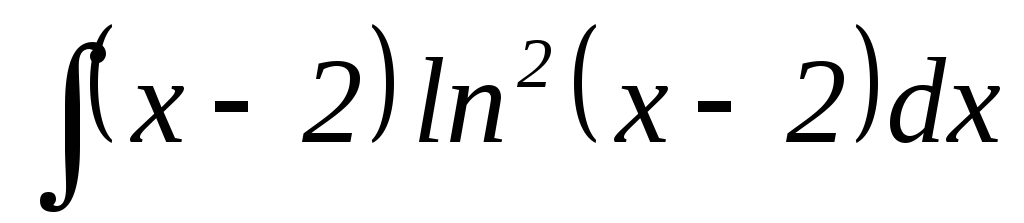 26.
26. 
 27.
27. 
 28.
28. 
Варіант 26
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 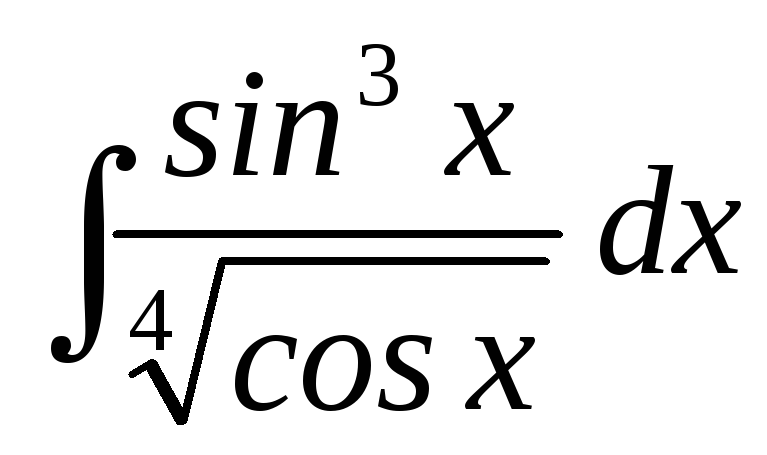
 20.
20. 
 21.
21. 
 22.
22. 
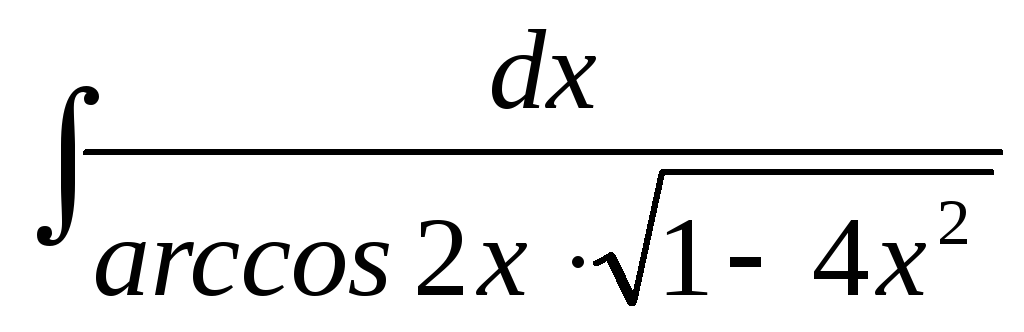 23.
23. 
 24.
24. 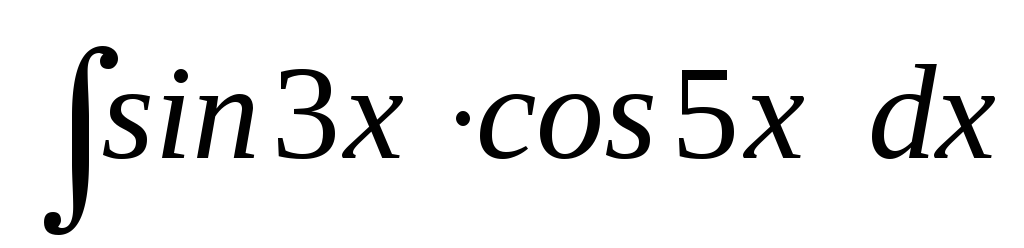
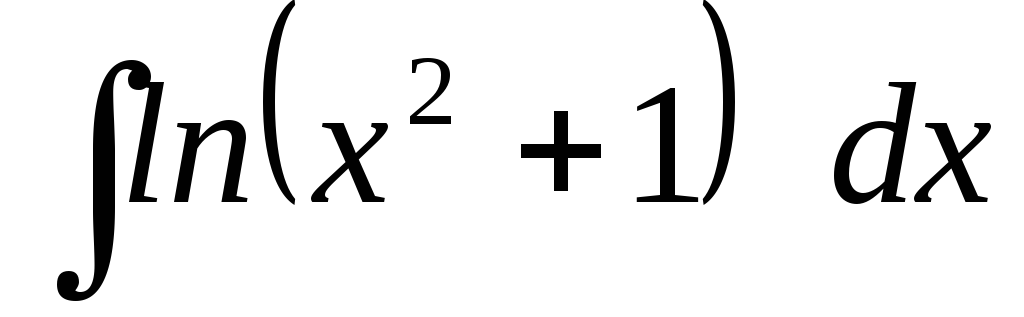 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 
Варіант 27
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
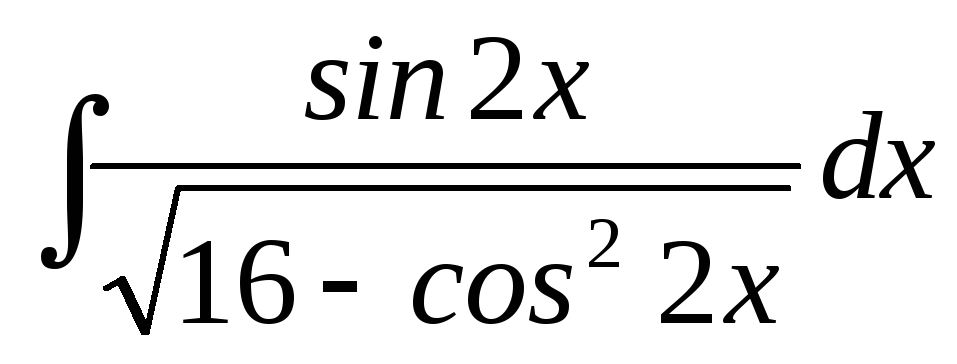 21.
21. 
 22.
22. 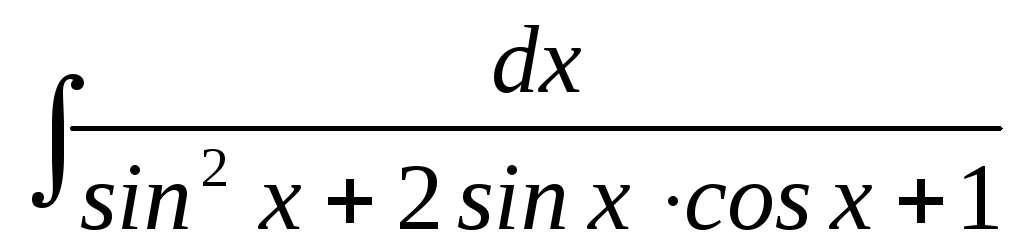
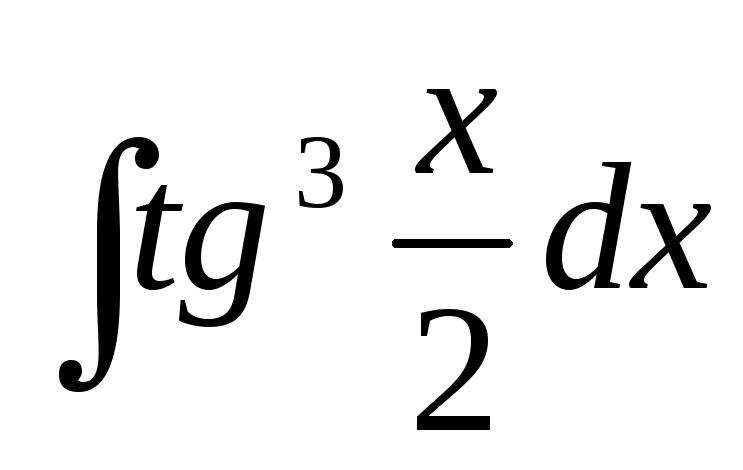 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 
Варіант 28
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 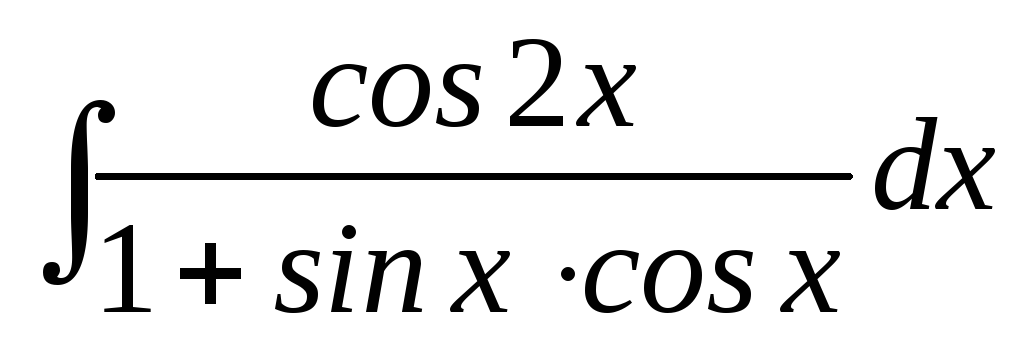
 26.
26. 
 27.
27. 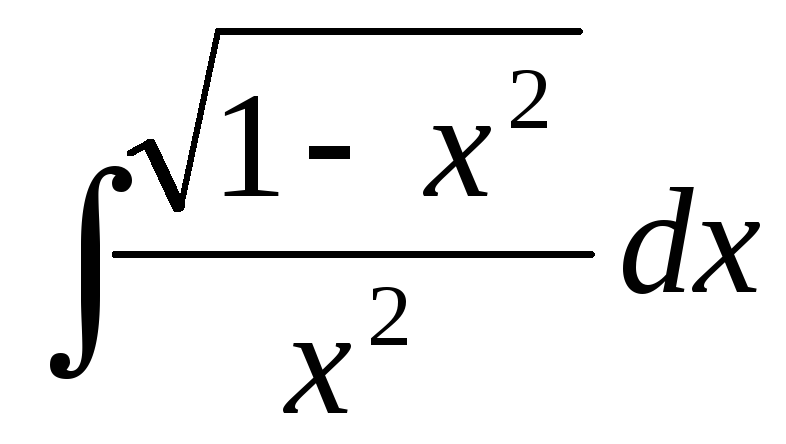
 28.
28. 
Варіант 29
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 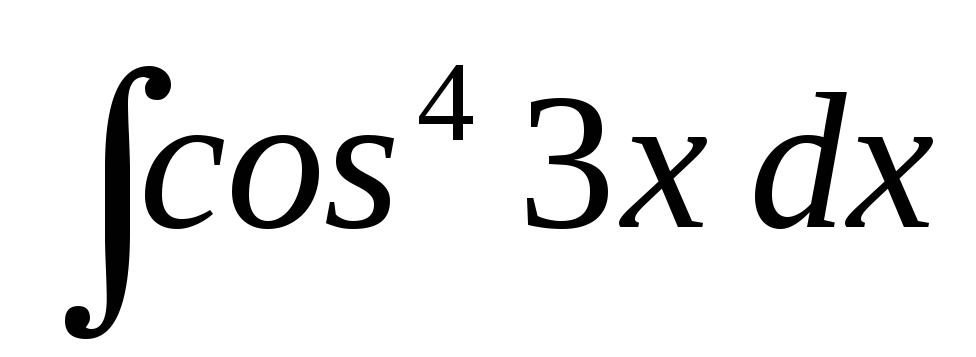
 20.
20. 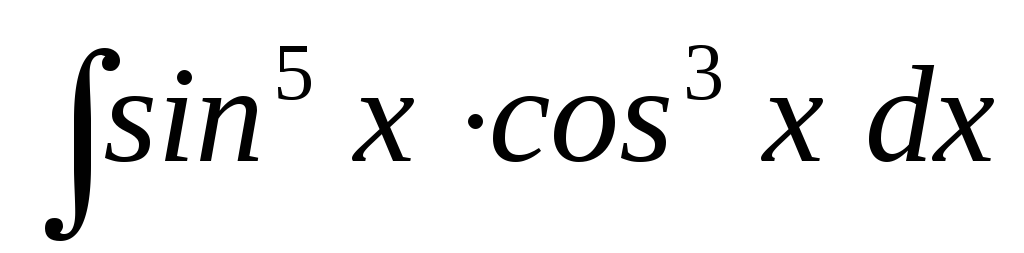
 21.
21. 
 22.
22. 
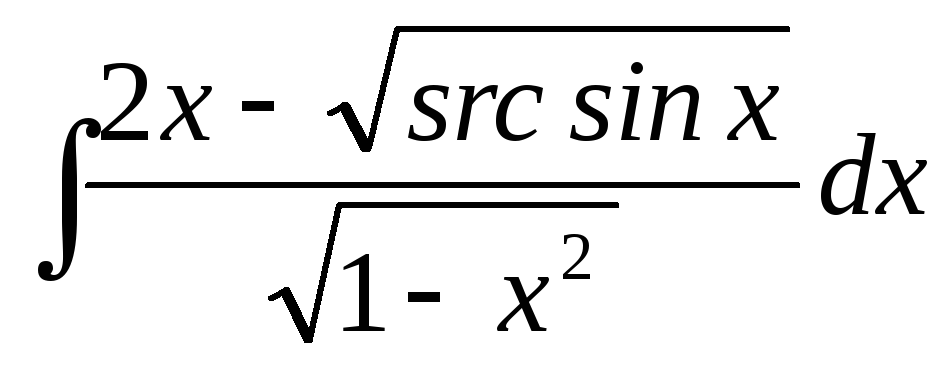 23.
23. 
 24.
24. 
 25.
25. 
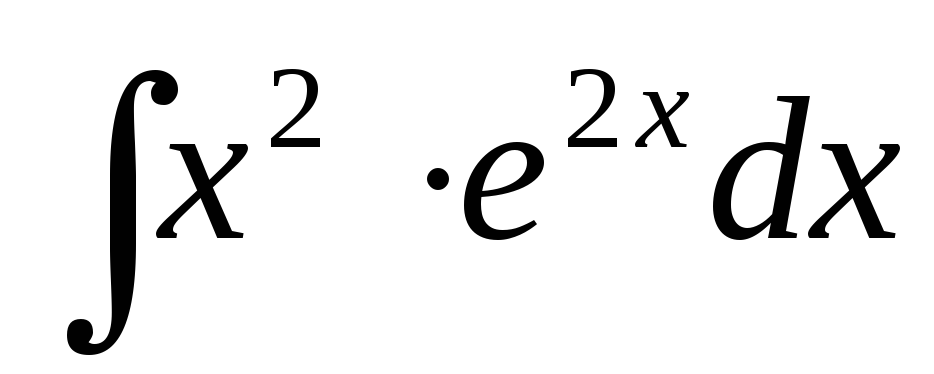 26.
26. 
 27.
27. 
 28.
28. 
Варіант 30
 15.
15. 
 16.
16.

 17.
17.

 18.
18. 
 19.
19. 
 20.
20. 
 21.
21. 
 22.
22. 
 23.
23. 
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 
