МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦИОНАЛЬНА МЕТАЛЛУРГІЙНА АКАДЕМІЯ УКРАЇНИ

Методичні вказівки та ідивідуальні завдання

ДО ТЕМИ “ДОСЛІДЖЕННЯ ПОВЕДІНКИ ФУНКЦІЇ ЗА ДОПОМОГОЮ ПОХІДНИХ ”

З КУРСУ “МАТЕМАТИКА ДЛЯ ЄКОНОМИСТІВ ”

ДЛЯ СТУДЕНТІВ I КУРСУ

ЄКОНОМИЧНИХ СПЕЦІАЛЬНОСТЕЙ

Дніпропетровськ НМетАУ2009

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦИОНАЛЬНА МЕТАЛЛУРГІЙНА АКАДЕМІЯ УКРАЇНИ

МЕТОДИЧНІ ВКАЗІВКИ ТА ІДИВІДУАЛЬНІ ЗАВДАННЯ

ДО ТЕМИ “ДОСЛІДЖЕННЯ ПОВЕДІНКИ ФУНКЦІЇ ЗА ДОПОМОГОЮ ПОХІДНИХ ”

З КУРСУ “МАТЕМАТИКА ДЛЯ ЄКОНОМИСТІВ ”

ДЛЯ СТУДЕНТІВ I КУРСУ

ЄКОНОМИЧНИХ СПЕЦІАЛЬНОСТЕЙ

Затверджено на засіданні

кафедри ПМ таОТ

Протокол № від

Дніпропетровськ НМетАУ2009

Методичні вказівки та ідивідуальні завдання до теми “ДОСЛІДЖЕННЯ ПОВЕДІНКИ ФУНКЦІЇ ЗА ДОПОМОГОЮ ПОХІДНИХ ”З КУРСУ “МАТЕМАТИКА ДЛЯ ЄКОНОМИСТІВ ”ДЛЯ СТУДЕНТІВ I КУРСУ ЄКОНОМИЧНИХ СПЕЦІАЛЬНОСТЕЙ / Укл. Коноваленков В.С., Заборова Т.М– Дніпропетровськ: НМетАУ, 2009. – с.

Відповідальний за випуск Г.Г.Швачіч, проф.

Методичні вказівки та ідивідуальні завдання

до теми “ДОСЛІДЖЕННЯ ПОВЕДІНКИ ФУНКЦІЇ ЗА ДОПОМОГОЮ ПОХІДНИХ ”З КУРСУ “МАТЕМАТИКА ДЛЯ ЄКОНОМИСТІВ ”ДЛЯ СТУДЕНТІВ I КУРСУ ЄКОНОМИЧНИХ СПЕЦІАЛЬНОСТЕЙ

Навчальне видання

Укладачі: В.С.Коноваленков канд. техн. наук

Т.М. Заборова

Редактор: Л.М. Тонкошкур

1.ПОНЯТТЯ ФУНКЦІЇ.ХАРАКТЕРІСТІКИ ФУНКЦІЇ.

блиця інтегралів

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

Теорема про інваріантність формул інтегрування

Найважливішим при знаходженні невизначеного інтеграла є таке твердження:

Якщо має місце формула то вона залишається справедливою й у випадку, коли замістьнезалежної змінної в цій формулі знаходиться будь-яка функція від якої можна взяти диференціал, тобто.

Пояснимо зміст цієї теореми на прикладі: тоді.

Корисними при рішенні конкретних прикладів є формули , які випливають з теореми про інваріантність формул інтегрування:

15. 

16. ,

17. 

18. 

19. 

Найпростіші прийоми і методи інтегрування

Безпосереднє інтегрування містить у собі використання таблиці інтегралів (1-19), властивостей невизначених інтегралів і тотожних перетворень.

Розглянемо приклади.

Приклад 1:

.

Якщо піднести до квадрата чисельник підінтегральної функції, а потім результат почленно поділити на знаменник, одержимо три інтеграли, кожний із яких є табличним:

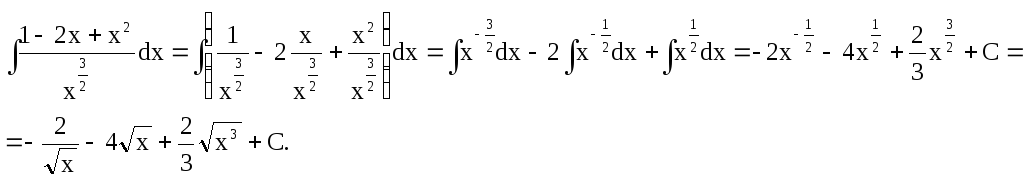
Вище використані відомі властивості: інтеграл від суми дорівнює сумі інтегралів, сталий множник можна виносити за знак інтеграла.

Приклад 2:

. Використання бінома Ньютона для розкладання підінтегральної функції практично неможливе. Скористуємося формулою 18 і формулою 1 таблиці інтегралів

Результат може бути отриманий, якщо вибрати такий шлях: ввести допоміжну змінну : тоді .

Використовуючи ці співвідношення і формулу 1 таблиці, отримаємо:

Той же результат отримаєм, якщ використаєм еквівалентні перетворення ,, де — стала.

Тоді

Під знак диференціала можна підводити сталий множник, перемінну інтегрування у будь-якому степені, а також різні функції. При цьому формули таблиці інтегралів застосовуються при інтегруванні не по x, а по допоміжній змінній інтегрування (теорема про інваріантність (незмінність) формул інтегрування). Наприклад, перша формула таблиці інтегралів залишається в силі, якщо неохідно знайти інтеграл, що має вигляд:

Аналогічно можна переписати інші формули таблиці інтегралів. Радимо проробити цю корисну вправу самостійно.

У ролі може виступати як лінійна функція, дивись розглянутий вище приклад, так і усяка інша елементарна функція.

Приклад 3:

.

Із формул 1 і 19 виходить:

Хід міркувань може бути і таким: інтеграл є табличним. Інтегралстане табличним, якщо замістьdx запишемо -1/5d (3-5x). Роздивимося ланцюжок очевидних рівностей (формула 19 таблиці):

.

Тоді

.

Аналогічний результат одержимо, якщо скористаємося підстановкою

Приклад 4:

Похідна знаменника підінтегральної функції дорівнюєтобто в чисельнику з точністю до множника (-1) маємо похідну знаменника. Використовуємо формулу 15 таблиці

Приклад 5:

таким чином, у чисельнику підінтегральної функції з точністю до множника (-16) маємо похідну підкореневого виразу знаменника. З формули 16 випливає:

Приклад 6:

Скористаємось тригонометричною тотожністю або

Далі, застосовуючи властивості невизначеного інтеграла і таблицю, одержуємо:

Розкладання підінтегрального виразу і виділення повного квадрата

Роздивимося інтеграли, у яких підінтегральна функція має вигляд дробу, у чисельнику якої - одиниця, а в знаменнику або квадратний тричлен, або корінь квадратний з нього. Почнемо з випадку раціональних дробів.

Приклад 7:

.

Знаменник підінтегральної функції - квадратний тричлен із позитивним дискримінантом. Отже, він має два дійсні різноманітні корені. У цьому випадку можна діяти таким чином: або уявити знаменник у вигляді добутку лінійних множників, а підінтегральну функцію уявити у вигляді суми найпростіших дробів, або виділити в знаменнику повний квадрат і призвести рішення до табличного інтеграла 14 .

Повернемося до приклада. Корені квадратного тричлена рівні 5 і 2. У такому випадку

Числа А и В називаються невизначеними коефіцієнтами. Для їхнього перебування складемо систему лінійних рівнянь (1). Для її отримання прирівняємо коефіцієнти при подібних членах у чисельниках першої й останньої дробів, що записані нижче:

Система лінійних рівнянь щодо А і В така:

(1)

Звідси

Шуканий інтеграл дорівнює сумі двох інтегралів:

Нехай тепер дискримінант квадратного тричлена менший нуля. У цьому випадку інтеграл приводиться до вигляду:+С.

Звернемося до конкретного приклада.

Приклад 8:

Нарешті, якщо дискримінант квадратного тричлена дорівнює нулю, то інтеграл приводиться до вигляду

Як бачимо, спосіб виділення повного квадрата є достатньо ефективним, тому що швидко призводить до результату. Якщо квадратний тричлен у знаменнику до того ж знаходиться під знаком квадратного кореня, то повний квадрат виділяється під знаком кореня, після чого застосовуються формули 9, 13 або 14 таблиці інтегралів.