Малиновський андрій едуардович

(1884-1937)

Працював над питаннями електронної теорії провідності металів. Довів неспроможність класичної теорії щодо розрахунку взаємодії вільних електронів і позитивних іонів у металах, представив свою інтерпритацію цієї взаємодії. Дав уточнення до теорії дослідів Толмена і Стюарта з приводу визначення питомого заряду електронів. Спростував точку зору Лоренца про інертність електронів провідності.

§60. Закон Відемана-Франца. Недоліки класичної електронної теорії провідності металів

У 1853 році німецькі вчені Відеман і Франц на основі експериментів встановили закон, згідно з яким:

для всіх металів при одній і тій самій температурі відношення коефіцієнта теплопровідності æ до коефіцієнта питомої електропровідності є величина стала:

.

Оскільки величини тазалежать від температури (неявно, а через середню арифметичну швидкість та швидкість теплового руху), то наступні дослід­ження Лоренца довели, що

.

Відомо, що теплопровідність металів переважно здійснюється за рахунок руху вільних електронів. Електронний газ в металах подібний до одноатомного ідеального газу. Тому згідно з молекулярно-кіне­тичною теорією коефіцієнт теплопровідності становитиме

звідси

,

де n – концентрація вільних електронів, – стала Больцмана.

Оскільки питома електропровідність

,

тоді

.

Середня кінетична енергія однієї молекули ідеального газу дорівнює

,

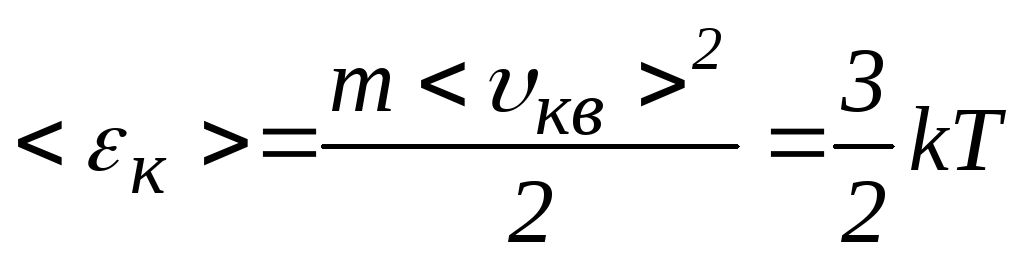де - середня квадратична швидкість.

Якщо знехтувати, як це зробив Друде, відмінністю між середньою швидкістю теплового руху і їхньою середньою квадратичною швидкістю, тобто припустити, що

,

тоді

.

Отже,

і .

Це значення добре узгоджується з дослідними даними.

Але це узгодження класичної електронної теорії з експериментом виявилось випадковим. Друде вважав, що всі елек­трони мають однакову швидкість теплового руху. Лоренц вдосконалив теорію Друде, застосувавши до електронного газу статис­тику Максвелла, тобто розподіл молекул за швидкостями. Виявилось, що в цьому разі

.

Коефіцієнт згідно з теорією Лоренца гірше узгоджується з дослідними даними, ніж результат Друде. Виявляється, що уточнена класична елек­тронна теорія, яка враховує статистичні властивості електронного газу в металах, гірше узгоджується з дослідними даними, ніж теорія Друде.

Спроби застосувати класичну електронну теорію Друде-Лоренца для пояснення ряду закономірностей електрики і теплових явищ, які спостерігаються на досліді, не завжди приводили до позитивних результатів. Нездатність класичної електронної теорії пояснити деякі закони і явища свідчать про її обмеженість. Розглянемо кілька таких прикладів.

І. Молярна теплоємність металу

Згідно з класичною електронною теорією молярна теплоємність металу дорівнює сумі молярної теплоємності кристалічної ґраткиі молярної теплоємностіелектронного газу, який може розглядатися як одноатомний ідеальний газ:

.

Іони, що утворюють кристалічну ґратку металу, здійснюють коливання біля вузлів ґратки. Кожний іон має три коли­вальні ступені вільності, на які в середньому припадає енергія . Внутрішня енергія моля іонів

.

Отже,

.

Молярна теплоємність електронного газу як ідеального

.

Отже, молярна теплоємність металів

.

Але експериментальні дані показують, що теплоємність металів, так само, як і теплоємність твердих діелектриків, близька до 3R. Отримали неочікуване і незрозуміле явище практичної відсутності теплоємності в електронного газу.