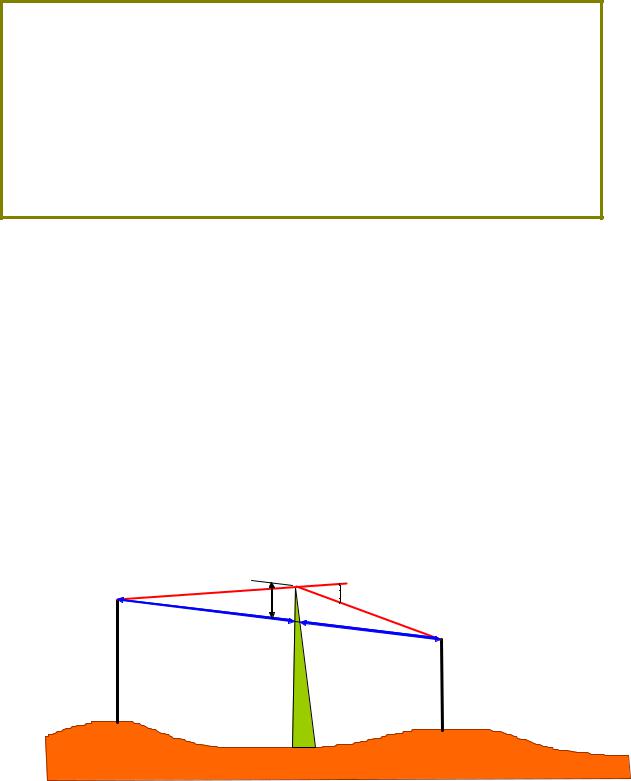
Упражнение 7
Мобильный приемник расположен на расстоянии 5 км от базовой станции и использует в качестве антенны четвертьволновый диполь. На расстоянии 1 км амплитуда электрического поля составила 10-3 В/м. Частота 900 МГц. Найти:
а) длину и усиление приемной антенны;
б) мощность на выходе приемной антенны Pr , если используется 2- лучевая модель распространения радиоволн. Высота подвеса излучающей антенны 50 м, приемной - 1.5 м.
7.1.2. Дифракция радиоволн
Явление дифракции позволяет радиоволнам распространяться вокруг сферической земной поверхности за горизонт и за различные препятствия. Несмотря на перекрытие прямой видимости и существенное уменьшение уровня сигнала, он все таки остается достаточным для приема.
Феномен дифракции объясняется принципом Гюйгенса – вторичного переизлучения точек фронта волны с различной фазой (зон Френеля). Напряженность поля определяется векторной суммой вклада вторичных излучателей.
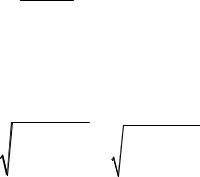
Пусть между излучателем и приемником расположено препятствие – экран высотой h бесконечных размеров в поперечном сечении. Расстояние от экрана до излучателя d1 , до приемника – d2 .
Передающая |
|
h |
α |
|
d1 |
|
|
||
антенна |
|
d2 |
Приемная |
|
|
|
|
||
|
|
|
|
антенна |
Рис. 7.7. Дифракция радиоволн на клиновидном препятствии
Ясно, что путь через кромку препятствия больше прямого. Полагая, что h<<d1,d2 и h>>λ, разность хода прямого и через кромку лучей будет:
103
|
∆ ≈ |
h2 |
d +d |
2 . |
|
|
(7.35) |
||
|
|
2 |
1 |
|
|
|
|||
|
|
|
d d |
2 |
|
|
|
||
|
|
|
|
1 |
|
|
|
||
Соответствующая ему разность фаз |
|
|
|
|
2 d +d |
|
|
||
Φ= |
2π∆ |
= |
2π h |
2 , |
(7.36) |
||||
λ |
|
|
|
1 |
|
||||
|
|
|
λ 2 d d |
2 |
|
||||
|
|
|
|
|
|
1 |
|
||
где используется приближение для малого аргумента |
tg x ≈ x, |
а угол α ап- |
|||||||
проксимирован выражением |
|
|
|
|
|
|
|
|
|
α≈ h d1+d2 .
d1d2
Выражение (7.36) может быть аппроксимировано с использованием безразмерного дифракционного параметра Френеля-Кирхгофа:
ν=h |
2(d1+d2 ) |
=α |
2d1d2 |
|
|
, |
(7.37) |
|
|
λ(d +d |
|
) |
|||||
|
λd d |
2 |
|
2 |
|
|
||
|
1 |
|
1 |
|
|
|
||
где α подставляется в радианах, все остальные параметры в метрах. Таким образом, разность фаз Ф может быть вычислена из выражения
Φ = |
π |
ν2 . |
(7.38) |
|
2 |
|
|
Из выражения (7.38) следует, что сдвиг фазы между прямым и дифракционным лучами является функцией высоты h и взаимного расположения препятствия, излучателя и приемника.
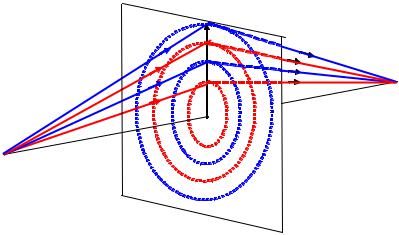
Дифракционные потери мощности в радиоканале могут быть объяснены с помощью зон Френеля. Зоны Френеля представляют собой области, разность хода через которые от излучателя до приемника составляет nλ/2 по сравнению
спрямым лучом (λ – длина волны, n – целое число).
Вмобильной связи обычно наблюдается затенение части зон (источников вторичных волн) и, следовательно, уменьшение доли принятой мощности. В зависимости от геометрии препятствия принятая энергия определяется через векторное суммирование вторичных волн.
104
h
Приемная
антенна
d2 1
Передающая d1 234 антенна
Рис. 7.8. Формирование зон Френеля
Если препятствие не затеняет первую зону Френеля, то дифракционные потери минимальны и ими пренебрегают. Используют следующее свойство: если открыто не менее 55% первой зоны Френеля, то дальнейшее открытие первой зоны Френеля не уменьшает дифракционные потери.
Определение степени ослабления поля холмами и зданиями является достаточно сложной задачей при расчете зон обслуживания. Обычно точный расчет ослабления невозможен, поэтому используют методы расчета поля с необходимыми экспериментальными поправками.
Препятствие в виде одиночного холма или горы может быть обсчитано с использованием модели клина. Это простейшая модель препятствия, и быстрый расчет ослабления возможен с использованием классического решения Френеля для дифракции поля на полуплоскости.
Напряженность поля в точке расположения приемной антенны определяется векторной суммой вторичных источников, лежащих в плоскости, расположенной над препятствием. Напряженность поля при дифракции на клине определяется выражением
Ed |
|
1+ j |
∞ |
− |
jπt2 |
|
|
|
|
2 dt , |
(7.39) |
||||||
= F(ν) = |
∫ e |
|
||||||
E0 |
2 |
|
|
|||||
|
|
ν |
|
|
|
|
||
где Е0 – напряженность поля в точке расположения приемной антенны при отсутствии препятствия и земли, а F(n) – комплексный интеграл Френеля. Значение интеграла F(n) определяется из графиков и таблиц.
105
излучающая |
|
приемная |
|
излучающая |
приемная |
||||
антенна |
α |
|
антенна |
антенна |
|||||
антенна |
|
|
|
|
|||||
|
h |
|
|
|
|
|
|
|
|
d1 |
d2 |
|
|
|
|
|
|
d1 |
d2 |
αиνположительны, |
|
|
|
|
|
|
αиνравны0, |
||
т.к. h>0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
т.к. h=0 |
|
излучающая |
|
|
|
|
|
|
приемная |
|
|
антенна |
d1 |
|
h |
d2 |
|
антенна |
|
||
|
αиνотрицательны, |
|
|
|
|||||
|
|
|
|
т.к. h<0 |
|
|
|
||
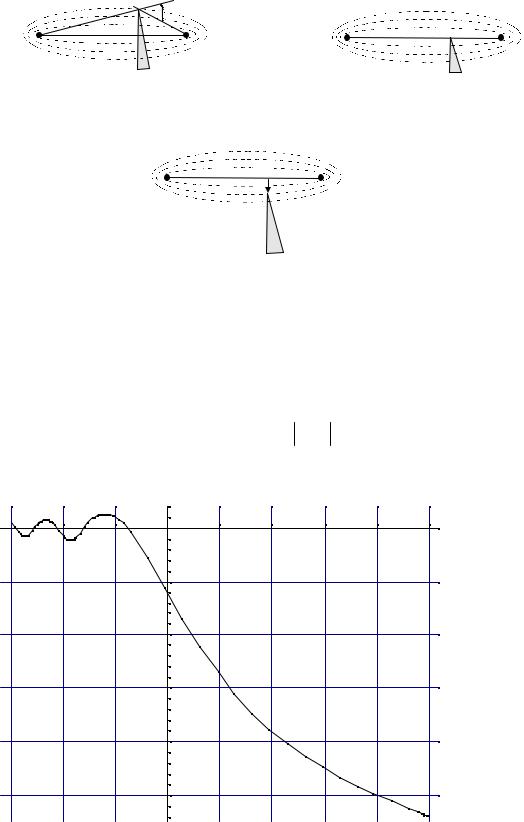
Рис. 7.9. Варианты перекрытия видимости антенн препятствием |
|||||||||
Коэффициент дифракционного усиления с препятствием (обычно он |
|||||||||
меньше 1) по сравнению со свободным пространством |
|
||||||||
|
|
G |
d |
= 20lg F(ν) , дБ. |
(7.40) |
||||
|
|
|
|
|
|
|
|
||
График этой функции показан на рис. 7.10. |
|
|
|||||||
Gd, дБ |
ν |
|
|
|
|
|
|
|
|
-2 |
-1 |
1 |
|
|
|
2 |
3 |
4 |
5 |
|
-5 |
|
|
|
|
|
|
|
|
|
-10 |
|
|
|
|
|
|
|
|
|
-15 |
|
|
|
|
|
|
|
|
|
-20 |
|
|
|
|
|
|
|
|
|
-25 |
|
|
|
|
|
|
|
|
Рис. 7.10. Зависимость коэффициента дифракционного усиления |
|||||||||
|
от значения параметра дифракции n |
|
|||||||
106
Приближенно можно считать:
G d = 0, дБ, |
ν ≤ −1; |
(7.41a) |
Gd = 20lg(0,5 −0,62ν), дБ, |
−1≤ν ≤ 0; |
(7.41б) |
|
|
|
d |
( |
|
|
|
) |
|
|
|
|
G |
|
= 20lg 0,5e−0,95ν , дБ, |
0 ≤ ν ≤1; |
(7.41в) |
||||
Gd = 20lg |
|
0,4- 0,1184-(0,38-0,1ν) |
2 |
|
, дБ, |
1≤ ν≤ 2,4; |
(7.41г) |
|||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Gd = 20 lg(0,225ν |
), |
|
дБ ν ≤ 2,4 |
(41д) |
|||
Упражнение 8
Вычислить дифракционные потери для 3 случаев перекрытия препятствием видимости передающей и приемной антенн (рис. 7.9). Поло-
жить λ = 1/3 м; d1 = 1 км; d2 = 1 км: a) h = 25 м;
б) h = 0;
в) h = -25 м.
Сравнить результат с графиком, приведенным на рис.7.10, а также с аппроксимирующим выражением (7.41).
Если на пути между излучателем и приемником имеется несколько препятствий, то все они аппроксимируются одним эквивалентным препятствием
(рис. 7.11).
Эта модель хорошо работает для двух препятствий, для нескольких - возникают определенные математические трудности.
107