
Конспект ТФКЗ
.pdf
Коші-Рімана для заданої дійсної частини аналітичної функції однозначно можна визначити повний диференціал невідомої уявної частини v x, y :
dv v dx v dy u dx u dy.
x |
y |
y |
x |
Це означає, що функція v x, |
y є визначеною з точністю до сталої. |
||
2. Нехай функція f z є |
аналітичною |
в області D і для z D |
|
v x,y Im f z const. Тоді для z D |
f z const. |
||
Доведення.
► Якщо функція f z аналітична для виконуються умови Коші-Рімана. Оскільки,
z D, то всюди в цій області v x, y Im f z K1 const, то
|
v |
|
v |
0. |
Це |
означає, |
|
що |
|
du |
|
u |
dx |
u |
dy 0, |
|
тобто |
для |
z D |
|||||||||||||||||
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|||||||
u x, y Re f z K2 const |
f z K1 iK2. ◄ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Приклад. Знайти аналітичну функцію |
|
f z , якщо Re f z y3 3yx2, |
|
f 0 i. |
||||||||||||||||||||||||||||||||
|
|
|
• З умов Коші-Рімана маємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
u |
6xy |
v |
, |
|
u |
3y2 3x2 |
v |
. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
y |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||||
|
|
|
З першої рівності отримаємо: |
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
v 6xy dy 3xy |
2 |
g x |
|
|
|
|
|
|
2 |
|
|
|
|
3y |
2 |
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
3y |
|
|
|
|
|
|
3x . |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
x |
|
|
g x |
|
|||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
g x x |
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
C . Отже, |
v 3xy |
x |
C , а |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Тоді g x 3x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
f z y3 3yx2 |
3ixy2 ix3 iC y3 |
3yx2 i x3 |
3xy2 iC iz3 iC . |
|||||||||||||||||||||||||||||||
|
|
|
З умови |
f 0 i знаходимо, |
що C 1 і |
f z iz3 |
i. • |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
§ 4. Конформні відображення. Геометричний зміст похідної |
|
|
|||||||||||||||||||||||||||||||
|
|
|
Нехай функція комплексної змінної w f z |
є аналітичною в точці z0 C |
||||||||||||||||||||||||||||||||
і f z0 0. Це означає, що в околі точки z0 |
існує неперервна похідна |
|
f z . |
|||||||||||||||||||||||||||||||||
Означення 1. Взаємно однозначне відображення, яке здійснюється функцією w f z у цьому випадку, називається конформним у точці z0.
Означення 2. Взаємно однозначне відображення, яке є конформним у кожній точці області D C , називається конформним в області D.
Припустимо, що функція комплексної |
змінної w f z здійснює |
відображення, конформне в точці z0, тобто |
f z0 A cos isin , де |
41
A |
f z0 |
0, |
а arg f z0 . |
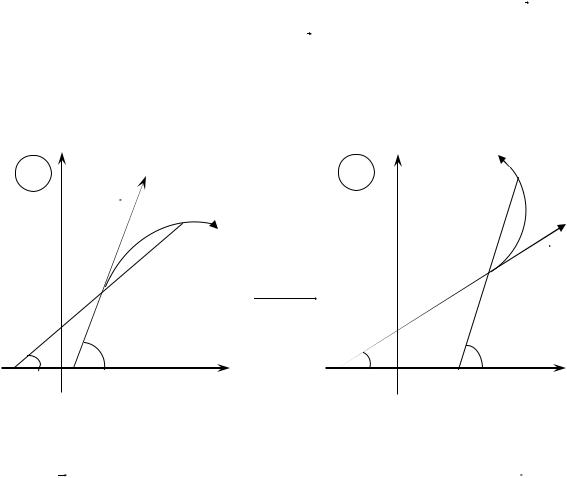
Розглянемо на площині C |
гладку |
криву з |
|||||||
початком у точці z0 |
(див. рис.). Позначимо z z z0, arg z, |
l – вектор, |
|||||||||||
дотичний до кривої в точці |
z0, |
0 |
argl. |
Припустимо, що точка |
z z0 z |
||||||||
прямує до точки z0 вздовж кривої : z , |
z z0. Тоді у площині w відповідна |
||||||||||||
точка w0 w f z0 |
z буде прямувати до точки |
w0 f z0 вздовж деякої |
|||||||||||
кривої , яка є образом кривої |
при відображенні w f z . |
|
|
|
|||||||||
|
|
Im z |
|
|
|
|
|
w |
Imw |
|
w |
||
|
z |
|
|
|
|
|
|
|
|||||
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
|
w f z |
|
|
|
|
|
l |
||
|
|
|
|
|
|
|
w0 |
|
|
||||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
O |
|
|
Rez |
|
|
|
O |
|
|
|
Rew |
|
|
Якщо точка |
z , z |
z0, то точка |
|
|
w w0 |
(оскільки |
||||||
|
w f z , |
||||||||||||
відображення |
конформне, |
тобто |
однозначне). |
Позначимо |
w w w0, |
||||||||
arg w, l f z0 :
звідки
– вектор, дотичний до кривої в точці w0 , 0 |
argl . Знайдемо |
|||||||||||||||||||||||
|
f z0 |
lim |
|
f z f z0 |
|
|
lim |
|
w |
, |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
z z0 |
|
z z0 |
z z0 z |
|
|
|
|||||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
iarg f z0 |
|
|
i |
|
|
|
|
|
|
|
w |
|
|
i |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f z0 |
|
e |
|
|
Ae |
|
|
lim |
|
|
z |
e |
|
|
|
, |
|
||||||
|
|
|
|
|
|
|
|
|
z z0 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
A lim |
|
w |
|
, |
|
|
|
|
|
|
|
|
|
|
(4.1) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
z z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
z
0 |
0 arg f z0 . |
(4.2) |
|||||||
Оскільки у формулі (4.1) права частина не залежить від вигляду і напрям- |
|||||||||
ку кривої , то лінійний розтяг |
k lim |
|
|
w |
|
|
в точці |
z0 є однаковим для всіх |
|
|
|
||||||||
|
|
|
|
|
|
||||
|
|
z |
|
|
|
||||
|
z z0 |
|
|
|
|
||||
42
кривих з початком у точці z0 і k |
f z0 |
A. |
Цю властивість називають |
властивістю постійності розтягу (чи стиску, |
якщо k 1) конформного |
||
відображення w f z в точці z0. Отже, геометричний зміст модуля похідної:
|
f z0 |
|
– лінійний розтяг в точці z0. |
|
|
w |
|
|
|
f z0 |
|
|
|
z |
|
o |
|
z |
|
, |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Оскільки для |
|
аналітичних функцій |
|
|
|
|
|
|
|
|
|
то при |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
конформному відображенні w f z коло |
|
z z0 |
|
|
|
z |
|
з точністю |
до o |
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
переходить в коло |
|
w w0 |
|
|
|
f z0 |
|
. Тому властивість постійності |
розтягу |
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
називають також круговою властивістю відображення w f z в точці z0.
Права частина формули (4.2) теж не залежить від вигляду кривої (та її
напряму, |
тобто вектора l ). Це означає, що кут arg f z0 повороту вектора |
|||||
l в точці z0 |
при конформному відображенні w f z є одним і тим же для всіх |
|||||
кривих |
з початком у точці |
z0. Отже, геометричний |
зміст |
аргументу |
||
похідної: |
arg f z0 – кут повороту кривих. |
|
|
|
||
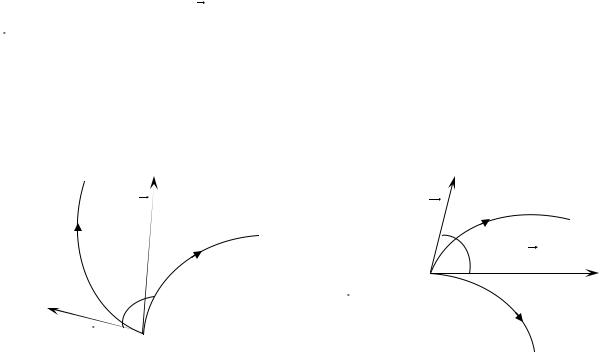
Кутом між кривими 1 і |
2, які мають спільний початок |
у точці z0, |
||||
називають кут між їх дотичними векторами. |
|
|
|
|||
2 |
|
l1 |
|
l2 |
2 |
|
|
|
|
|
|||
|
|
1 |
|
|
l1 |
|
|
|
|
|
|
||
|
|
|
w f z |
w0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
||
|
l2 |
z0 |
|
1 |
|
|
|
|
|
|
|
||
Оскільки при конформному відображенні w f z всі криві з початком у |
||||||
точці z0 |
повертаються на один і той же кут |
arg f z0 , то при такому |
||||
конформному відображенні кут між кривими 1 |
і 2 (як кут між дотичними |
|||||
векторами) |
в точці z0 буде дорівнювати куту між кривими |
1 і |
2 в точці |
|||
w0 f z0 |
як за абсолютною |
величиною, так |
і за напрямком відліку. Цю |
|||
властивість називають властивістю збереження кутів. |
|
|
||||
Отже, якщо функція w f z аналітична в точці z0 і |
f z0 0, то всі |
|||||
криві площини z, які проходять через точку z0 |
і мають дотичні в цій точці, |
|||||
за допомогою функції w f z |
відображаються на криві площини w, які |
|||||
проходять через точку w0 f z0 і також мають дотичні в цій точці,
причому кути між кривими у площині z і кути між їх відображеннями на площину w зберігаються як за величиною, так і за напрямом їх відліку.
Конформні відображення є відображеннями локальної подібності.
43
Основні принципи конформних відображень
Нехай функція комплексної змінної w f z визначена в області D. З’я- суємо, які умови повинна задовольняти функція комплексної змінної w f z , щоб вона здійснювала конформне відображення області D на область E.
Теорема 4.1. (Достатні умови конформності відображень). Нехай функція
w f z |
– однолиста і аналітична в області |
D і |
|
|
f z 0 для |
||||
z D. Тоді відображення w f z є конформним в області D. |
||||
Доведення. |
z 0, то відображення |
w f z |
|
|
|
має |
властивість |
||
► Оскільки f |
||||
збереження кутів та сталості розтягу, тобто є конформним у кожній точці області D. Однолистість функції w f z в області D забезпечує однозначне відображення області D на область E значень функції w f z . Отже, відображення w f z є конформним в області D. ◄
Теорема 4.2. (Необхідні умови конформності відображень). Якщо функція w f z , яка здійснює конформне відображення області D на область E комплексної площини, є обмеженою в області D, то вона є однолистою і аналітичною в області D і при цьому f z 0 для z D.
Доведення.
► Оскільки функція w f z є обмеженою для z D, то для z D і
z z D |
існує скінчений |
приріст |
w f z z f z . |
Відображення |
|||||||||||||
w f z є конформним в області D, |
тому для всіх z D існує |
|
w |
|
A 0 (з |
||||||||||||
|
|
||||||||||||||||
|
z |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
точністю до |
o z ) і, відповідно до властивостей збереження кутів та сталості |
||||||||||||||||
розтягу, існує arg |
w |
. Звідси отримуємо, що |
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
z |
|
w |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
A cos isin |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
z |
|
|
w |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
з точністю до o z , що означає, що |
lim |
|
A cos isin |
|
|
||||||||||||
|
|
||||||||||||||||
|
f z . |
||||||||||||||||
|
|
A 0, |
то f |
|
z 0 z |
|
|
|
|
||||||||
Оскільки |
для |
z D. Внаслідок |
конформності, |
||||||||||||||
z 0 |
|||||||||||||||||
відображення |
w f z |
є однозначним, |
тому функція w f z |
є однолистою |
|||||||||||||
всюди в області D. ◄ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Теорема 4.3. Для того, щоб функція w f z здійснювала конформне відображення області D, необхідно і достатньо, щоб функція f z була однолистою і аналітичною в області D і f z 0 для z D.
44
І. Принцип взаємно однозначної відповідності границь.
Теорема 4.4. Нехай в обмеженій однозв’язній області D, межа якої , задано однозначну аналітичну функцію w f z , яка неперервна у площині w і здійснює взаємно однозначне відображення контуруна деякий контур Γ комплексної площини w. Тоді, якщо для заданого відображення контурів зберігається напрям обходу, то функція w f z реалізує конформне відображення області D на внутрішню область G, обмежену контуром Γ .
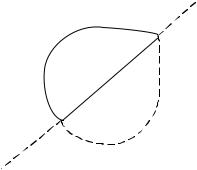
ІІ. Принцип симетрії.
D |
|
D
Нехай область D обмежена контуром , в який входить прямолінійна ділянка (скінчений чи не-
скінченний інтервал) . Область D , отримана дзеркальним відображенням області D відносно прямої, на якій лежить , називають
симетричною до області D відносно .
Теорема 4.5. (Принцип симетрії Рімана-Шварца). Нехай D – область,
обмежена контуром , який містить інтервал , і нехай на множині D визначено функцію комплексної змінної w f z , яка здійснює конформне відображення області D на область E комплексної площини w так, що інтервал межі переходить в
інтервал Γ межі Γ області |
E. Визначимо в точках z області |
|||||||||||||
D функцію |
|
f z |
за |
таким правилом: точка |
w f z |
|||||||||
симетрична до точки w f z відносно Γ , якщо точка |
z D є |
|||||||||||||
симетричною до точки z D, |
|
і f z f z , якщо |
z z . |
|||||||||||
Тоді функція |
f z |
є |
аналітичною в області D |
і |
здійснює |
|||||||||
конформне відображення області D на область |
E , яка |
|||||||||||||
симетрична до області E відносно Γ . Функція |
|
|
||||||||||||
f z , |
|
|
z |
|
, |
z D; |
|
|
|
|||||
|
z |
f |
|
|
z |
|
z, |
|
|
|
||||
w f |
|
|
|
z ; |
|
|
||||||||
|
|
z |
|
, |
|
|
|
|
z |
|
D |
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
||||
здійснює конформне відображення області D D на E Γ E . Важливою проблемою конформних відображень є проблема існування
функції комплексної змінної, яка здійснює конформне відображення області D в область E. Існування такої функції забезпечується теоремою Рімана.
45

Теорема Рімана. Довільну однозв’язну область D комплексної площини z, межа якої складається більше, ніж з однієї точки, можна конформно ві-дображати на внутрішність одиничного круга w 1
площини w. Функція w f z , яка здійснює таке відображення
так, що f z0 w0 і arg f z0 0 (де z0 D і 0 задане дійсне число) є єдиною.
Зауваження. Остання умова може бути замінена умовою відповідності трьох
граничних точок межі |
області D трьом точкам кола |
w |
1. |
|
|
||||||||||||
Найпростішими прикладами функцій, які здійснюють конформні |
|||||||||||||||||
відображення є дробово-лінійна функція і функція Жуковського. |
|
|
|||||||||||||||
Якщо |
z0 |
і |
w0 f z0 0, то відображення, |
|
яке |
здійснюється |
|||||||||||
функцією w f z |
називається конформним в точці z0, якщо є конформним |
||||||||||||||||
відображення, яке здійснюється функцією w f |
1 |
|
z 0. |
|
|||||||||||||
|
|
|
|
в точці |
|
||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
||||||
Якщо |
z0 , а |
w0 f z0 , то відображення, |
|
яке |
здійснюється |
||||||||||||
функцією w f z , |
називається конформним в точці z0, |
якщо в точці z0 є |
|||||||||||||||
конформним відображення, яке здійснюється функцією w |
|
1 |
|
. Якщо z0 |
|||||||||||||
|
f z |
||||||||||||||||
і w0 f z0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
w f z , |
|||
то |
відображення, яке здійснюється функцією |
||||||||||||||||
називається |
конформним в точці z0, якщо |
|
|
в точці |
z0 є конформним |
||||||||||||
відображення, яке здійснюється функцією w |
|
1 |
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
f |
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
||||||
46

ЛЕКЦІЯ 5
Інтеграл у комплексній площині
§ 1. Означення інтеграла від функції комплексної змінної. Теорема існування. Основні властивості інтеграла
Нехай функція комплексної |
змінної w |
f z u iv |
є неперервною в |
||||||||||||||||||||||||||||
деякій |
|
області |
D C |
і |
в |
цій |
області |
D |
задана кусково-гладка |
крива |
|||||||||||||||||||||
Γ z |
|
|
z z t , t , , де |
z0 z , |
|
|
z z – початкова і кінцева точки |
||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
кривої |
|
|
відповідно. |
Побудуємо |
|
|
|
довільне |
розбиття |
відрізка |
, : |
||||||||||||||||||||
t0 t1 ... tn |
і |
введемо |
|
|
|
такі |
позначення |
zj z tj , |
j |
|
, |
||||||||||||||||||||
|
|
|
0,n |
||||||||||||||||||||||||||||
j z |
|
z z t , t tj 1,t j , |
|
j |
|
|
|
|
|
– |
деяка |
дуга кривої z t . Очевидно, що |
|||||||||||||||||||
|
|
1,n |
|
||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Γ j . Таке |
розбиття |
кривої |
|
Γ |
будемо |
позначати |
буквою |
T . |
Число |
||||||||||||||||||||||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
T max j |
|
, 1 j n |
називають |
|
|
|
діаметром |
розбиття |
T . |
Покладемо |
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
zj zj |
zj 1. Очевидно, що |
|
zj |
|
|
|
j |
|
. Виберемо на кожній дузі j довільну |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
точку j |
і побудуємо інтегральну суму |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
T f j zj. |
|
|
(1.1) |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Якщо існує скінчена границя |
|
|
lim |
|
|
|
I , |
|
|
|
(1.2) |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
яка не залежить ні від способу розбиття кривої Γ , ні від вибору точок j , то її називають інтегралом від функції w f z вздовж кривої Γ і позначають
(1.3)
Існування границі тут означає, що
0 0: T ( вибору j ) T T I . (1.4)
Обчислення інтеграла (1.3) зводиться до обчислення відомих з курсу математичного аналізу криволінійних інтегралів другого роду. Справді, оскільки
zj zj zj 1 xj i yj; f j u j, j iv j, j , де j j i j , то
n |
n |
|
T f j zj u j, j iv j, j xj i yj |
(1.5) |
|
j 1 |
j 1 |
|
47
n |
n |
u j, j xj v j, j yj i u j, j yj v j, j xj , |
|
j 1 |
j 1 |
де |
|
n |
n |
Re T u j, j xj v j, j yj ,Im T u j, j yj v j, j xj |
|
j 1 |
j 1 |
є інтегральними сумами криволінійних інтегралів другого роду:
u x,y dx v x,y dy, |
u x,y dy v x,y dx. |
Γ |
Γ |
Перейшовши до границі, отримуємо, що
|
f z dz u x,y dx v x,y dy i u x,y dy v x,y dx. |
(1.6) |
|
Γ |
Γ |
Γ |
|
Існування криволінійних інтегралів (1.6) є необхідною і достатньою умовою існування інтеграла (1.3). Оскільки для існування криволінійних інтегралів (1.6) достатньо неперервності функцій двох змінних u x, y Re f z ; v x, y Im f z , то інтеграл (1.3) від функції комплексної змінної f z існує, якщо вона є неперервною на кривій .
З властивостей криволінійних інтегралів другого роду випливають такі властивості інтеграла (1.3):
1. Для 1, 2 C та f1 z , f2 z , неперервних на Γ ,
1 f1 z 2 f2 z dz 1 f1 z dz 2 f2 z dz.
Γ |
Γ |
Γ |
2. Якщо Γ Γ1 Γ2, а f z – неперервна на Γ , то
f z dz f z dz f z dz.
|
|
|
|
|
|
Γ |
|
Γ1 |
|
|
Γ2 |
|||
3. |
|
|
|
|
|
|
|
f z dz f z dz. |
||||||
|
|
|
|
|
|
|
Γ |
Γ |
||||||
4. |
|
|
|
|
|
|
|
f z dz |
|
|
f z |
|
dl , |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Γ |
|
Γ |
||||
|
|
|
|
|
|
|
|
|
||||||
де |
|
dz |
|
|
dx 2 dy 2 |
dl |
– елемент |
довжини дуги Γ , а інтеграл справа є |
||||||
|
|
|||||||||||||
криволінійним інтегралом першого роду. Справді, з нерівності трикутникаz1 z2 z1 z2 маємо
|
|
n |
|
n |
|
|
|
|
|
|||
f z dz |
|
lim f j zj |
|
lim |
f j |
|
zj |
|
|
f z |
|
dl. |
|
|
|||||||||||
Γ |
|
T 0 j 1 |
|
T 0 j 1 |
|
|
|
Γ |
||||
Якщо для z Γ виконується нерівність f z M , то
48

f z dz M dl M Γ .
ΓΓ
5.Якщо Γ – гладка крива, то має місце формула:
f z dz f z t ztdt .
Справді, скориставшись формулою (1.6), маємо
f z dz u x t ,y t xt v x t ,y t yt dt
i u x t ,y t yt v x t ,y t xt dt
|
|
|
u t xt iu t yt iv t xt v t yt dt u t zt iv t zt dt f z t z dt.
|
|
|
Більше того, має місце формула заміни змінної
f z dz f d ,
ΓΓ
де z – аналітична функція, яка здійснює конформне відображення кривої
Γ на криву Γ . |
f z 1, z0, z |
|
|
Приклад 1. Нехай |
- точки початку і кінця гладкої кривої Γ . |
||
Показати, що dz z z0 . |
|
||
|
Γ |
|
|
• Побудуємо інтегральну суму |
|
||
n |
n |
|
... zn zn 1 zn z0 z z0.• |
T f j zj zj z1 z0 z2 z1 |
|||
j 1 |
j 1 |
|
|
Зауваження. Якщо крива Γ замкнена, то dz 0. |
|||
|
|
Γ |
|
Приклад 2. Обчислити інтеграл |
Imzdz, |
де Γ – пряма, що з’єднує точки |
|
|
|
Γ |
|
z 0, z 1 3i.
49
|
Im z |
• Оскільки |
Im z y, |
то |
Imzdz |
ydz. Параметрич- |
|||||||||||
|
|
|
|
|
|
|
Γ |
Γ |
|
|
|
|
|
|
|
|
|
|
|
|
не рівняння прямої Γ |
|
y 3x; |
|
|
|
|
|
|
||||||
3 |
|
|
має вигляд |
|
|
|
|
|
Тоді |
||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x x. |
|
|
|
|
|
|
|
|||
|
|
|
z x 3ix x 1 3i ; dz 1 3i dx; |
x 0;1 . Тому |
|||||||||||||
|
|
|
|
|
1 |
|
|
3 |
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 1 |
Rez Imzdz ydz 3x 1 3i dx 1 3i |
|
x2 |
|
|
|
1 3i . • |
||||||||||
|
|
|
|||||||||||||||
|
|
|
Γ |
Γ |
0 |
|
|
2 |
|
0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Приклад |
3. Обчислити |
I z z0 n dz, |
де C – |
коло |
|
|
z z0 |
|
, яке |
||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
обходиться проти годинникової стрілки, тобто
C z C, z z0 , 0 2 .
• Запишемо |
параметричне |
рівняння |
цього кола: z z0 |
ei , де |
|
0;2 ; dz i ei d . Тоді |
|
|
|
||
|
2 |
2 |
2 i, |
n 1; |
|
I z z0 ndz neni i ei d i |
|||||
n 1ei n 1 d |
n 1. |
||||
C |
0 |
0 |
0, |
||
|
|
||||
Як бачимо, обчислений інтеграл не залежить ні від радіуса кола ні від точки z0 (центра кола) і відмінний від нуля лише у випадку n 1. Це означає, що
|
dz |
|
2 i. • |
z z |
0 |
||
C |
|
|
§ 2. Теорема Коші
Теорема Коші. Якщо функція комплексної змінної w f z аналітична в однозв’язній області D, то
 f z dz 0,
f z dz 0,
Γ
де Γ – довільний кусково-гладкий замкнений контур, який повністю належить області D.
Доведення.
► Оскільки функція w f z u iv є аналітичною всюди всередині області , обмеженої контуром Γ , то функції u x,y , v x,y мають неперервні частинні похідні в області . Тому, згідно з означенням (1.3),
 f z dz
f z dz  u x,y dx v x,y dy i
u x,y dx v x,y dy i u x,y dy v x,y dx.
u x,y dy v x,y dx.
Γ |
Γ |
Γ |
Застосуємо до криволінійних інтегралів другого роду формулу Гріна:
50
