
Конспект ТФКЗ
.pdfЛЕКЦІЯ 3
Функції комплексної змінної
§1. Функція комплексної змінної. Обернена та складена функції. Геометрична інтерпретація
Нехай D C – деяка область комплексної площини |
C (або, взагалі |
||||
кажучи, деяка множина комплексних чисел). |
|
||||
Означення. |
Функцією комплексної змінної z |
|
|||
|
|
|
|
w f z , |
(1.1) |
|
яка задана |
в |
області D, називається закон, |
який кожному |
|
|
значенню z |
з області D ставить у відповідність одне або декілька |
|||
|
комплексних чисел w E. |
|
|||
Множину E комплексних чисел w, яка відповідає всім z D, називають |
|||||
множиною значень функції |
w. |
|
|||
Якщо |
кожному |
значенню z D ставиться у відповідність лише одне |
|||
комплексне |
число |
w E, |
то функція називається однозначною. У |
||
протилежному випадку функція називається багатозначною. |
|
||||
Оскільки комплексне число характеризується парою дійсних чисел, то і
функцію w f z |
комплексної змінної z x iy можна подати у вигляді |
|
|
|
w f z u x,y i v x,y , |
де u u x,y Rew; |
v v x,y Imw. |
|
Якщо закон |
w f z встановлює однозначну відповідність між облас- |
|
тями D і E комплексної площини C, то в області E можна визначити функцію комплексної змінної w:
z f 1 w g w , |
(1.2) |
яку називають оберненою до функції w f z . Умови існування оберненої функції сформулюємо пізніше.
Оскільки функція комплексної змінної w f z задається парою дійсних функцій u u x, y та v v x, y , то характер поведінки функції комплексної змінної не можна ілюструвати за допомогою відносно простого графіка у декартовій системі координат, як у випадку функції дійсної змінної. Для з’ясування геометричного змісту функції w f z розглянемо поряд з площиною z x iy ще одну площину комплексної змінної w u iv. Згідно з означенням, функція w f z , є законом відповідності (поки що однозначної) між точками z з координатами x, y і точками w з координатами u,v , а тому
21
геометричний зміст однозначної функції комплексної змінної w f z
полягає в тому, що вона відображає область D на областьE.
Приклад. Нехай задано функцію комплексної змінної w z2, яка визначена в
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
області |
D z: |
z |
1; 0 argz |
|
|
|
– чверть |
одиничного кола на |
||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
площині z ei (рис.1). Побудувати область E. |
|
|||||||||||||||||||||||||||
|
|
Im z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Imw |
|
|||||||||||
|
|
|
D |
1 |
|
|
w z2 |
|
|
|
|
|
|
|
|
|
|
E |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Rew |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
O |
|
|
|
|
Re z |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Рис.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
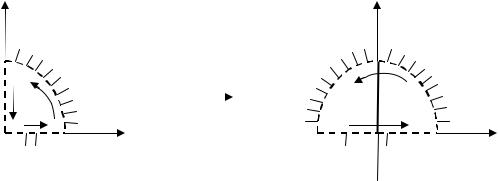
► Щоб побудувати область E, будемо обходити межу області D, починаючи з точки z 0 в додатному напрямку і встановимо, у що перейде ця
межа на площині w u iv rei . Оскільки w z2, то r 2, 2 , звідки
випливає, що |
відрізок 0 1, 0 дійсної осі z |
перейде |
у відрізок |
||||||
0 r 1, 0 |
дійсної осі площини w; чверть кола 1, |
0 |
|
|
– у півколо |
||||
|
|||||||||
|
|
|
|
|
2 |
|
|
||
r 1, 0 ; відрізок уявної осі 0 1, |
|
– у відрізок 0 r 1, |
|||||||
|
|||||||||
|
|
2 |
|
|
|
|
|
||
від’ємної дійсної осі площини w; кожна |
внутрішня точка області D – у |
||||||||
внутрішню точку області E і при цьому область E заповниться без ”дірок“
(рис.2).◄.
Дамо означення складеної функції комплексної змінної.
Означення. Суперпозиція однозначних функцій комплексної змінної w f h , h g z , називається складеною функцією комплексної змінної z : w f g z .
§2. Границя функції комплексної змінної. Основні теореми про границю функції. Границя по множині точок
Введемо тепер |
по аналогії з математичним аналізом поняття границі |
|||||||
функції комплексної |
змінної w f z . |
Нехай |
функція w f z |
визначена у |
||||
проколеному околі точки z0, тобто у |
кільці |
D:0 |
|
z z0 |
|
R. |
Розглянемо |
|
|
|
|||||||
22

довільні послідовності |
zn 1 , границя яких |
lim zn z0. |
Такі |
послідовності |
||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||
породжують послідовності wn 1 ; wn f zn значень функції w f z . |
||||||||||||||||||
Означення 1. |
Комплексне число |
w0 i |
називається границею функції |
|||||||||||||||
|
w f z |
в точці z0, |
якщо, незалежно від вибору |
збіжної до z0 |
||||||||||||||
|
послідовності zn 1 , |
zn D, послідовність |
wn 1 ; wn f zn |
|||||||||||||||
|
збігається до w , тобто з |
умови |
lim z |
n |
z |
0 |
випливає, що |
|||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||
|
lim w w . Записують це у вигляді |
|
|
|
|
|
|
|
||||||||||
|
n n |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim f z w0 |
i . |
|
|
|
|
|
|
(2.1) |
||||||||
|
|
z z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зауважимо, що при такому означенні точка z0 |
не обов’язково є точкою, в |
|||||||||||||||||
якій функція w f z визначена. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Означення 2 (границя по Коші). Число w0 |
називається границею функції |
|||||||||||||||||
|
w f z в точці z0, якщо: |
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
0: z D 0 |
|
z z0 |
|
|
|
|
|
|
f z w0 |
|
. |
(2.2) |
|||||
|
|
|
|
|||||||||||||||
Дане означення, на відміну від попереднього, має сенс лише для скінчених z0 і w0 z0 , w0 . Ці означення еквівалентні.
Введені означення границі формально нічим не відрізняються від означень границі функції дійсної змінної, тому залишаються справедливими теореми про границю суми, добутку, частки тощо.
Для функцій комплексної змінної існування границі (2.1) еквівалентне
існуванню двох границь |
lim |
u x,y , |
|
|
|
lim |
|
v x,y , причому |
||||||||||||||||
|
|
|
x, y x0, y0 |
|
|
|
|
x, y x0,y0 |
|
|
|
|
|
|
|
|||||||||
lim f z |
lim |
|
u x,y i |
lim |
v x,y i . |
|||||||||||||||||||
z z0 |
x, y x0, y0 |
|
|
|
|
|
x, y x0, y0 |
|
|
|
|
|
|
|
||||||||||
Якщо |
lim |
f z 0, то кажуть, що функція |
f z |
|
|
є нескінченно малою. |
||||||||||||||||||
|
z z0 |
|
|
|
f z є нескінченно великою (по модулю). |
|||||||||||||||||||
Якщо lim |
f z , то функція |
|||||||||||||||||||||||
z z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w f z визначена лише в |
||||||||
Зауваження. Якщо точка z0 |
є межовою, |
а функція |
||||||||||||||||||||||
області D (тобто у внутрішніх точках), |
то в означенні (2.2) під |
,z0 - |
||||||||||||||||||||||
околом точки розуміють ті точки околу, які належать області D. |
|
|
|
|
||||||||||||||||||||
Нехай функція |
w f z |
є визначеною в околі |
нескінченно віддаленої |
|||||||||||||||||||||
точки z0 розширеної комплексної площини |
|
|
|
, тобто в області |
|
z |
|
R0. Тоді |
||||||||||||||||
C |
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||
граничну рівність |
lim |
f z A символічно записують так: |
|
|
|
|
||||||||||||||||||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 R R R0 : |
|
z |
|
R |
|
|
|
f z A |
|
. |
(2.3) |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
23

§ 3. Неперервність функції комплексної змінної в точці. Функції, неперервні у замкненій області. Однолисті функції. Основні теореми про неперервні функції. Рівномірна неперервність
Означення 1. Функція w f z , визначена в точці z0 x0 iy0 та її околі, на-
|
зивається неперервною в точці z0, якщо |
|
|
lim f z f z0 : |
||||||
|
|
|
|
|
|
z z0 |
||||
lim |
f z f z0 0 0: z: |
|
z z0 |
|
|
|
|
f z f z0 |
|
(3.1) |
|
|
|
|
|||||||
z z0 |
Неперервність функції комплексної змінної w f z u x, y iv x, y у |
|||||||||
|
||||||||||
точці |
z0 є еквівалентною неперервності двох дійсних функцій двох змінних |
|||||||||
u x, y та v x, y в точці x0, y0 . |
|
|
|
|
|
|||||
|
Якщо функція w f z визначена і неперервна у кожній точці z D, то її |
|||||||||
називають неперервною в області D. Функцію w f z називають неперерв-
ною у замкненій області D D D, якщо умови означення 1 виконуються для всіх внутрішніх і межових точок з обумовленням побудови -околу межових точок.
Введемо поняття приросту z z z0 x i y комплексної змінної z і приросту функції w f z f z0 f z0 . Тоді можна сформулювати ще одне означення неперервності функції w f z у точці z0.
Означення 2. Функція w f z називається неперервною у точці z0, якщо
lim f z0 0 |
(3.2) |
z 0 |
|
Якщо точка z0 є межовою, тобто z0 D, то прирости |
z z z0 |
будуються тільки для тих точок z, які належать області D. |
|
Приклад 1. Довести, що функція w Rez є неперервною для всіх точок z C.
вольняє умову w x z . Це означає, що lim w 0 . Оскільки точка z0 є |
|||
▪ |
Розглянемо довільну точку z0 і побудуємо |
приріст z z z0 |
. Тоді |
приріст |
функції w Rez Rez0 Re z0 z Rez0 |
x0 x x0 x |
задо- |
z 0
довільною точкою комплексної площини, то функція w Rez є неперервною на всій комплексній площині C. ▪
Поняття неперервності функції комплексної змінної w f z , згідно з означенням, тісно пов’язане з неперервністю її дійсної u x, y та уявної v x, y частин за сукупністю змінних x, y . Це дозволяє перенести на функції комплексної змінної основні властивості неперервних функцій двох дійсних
змінних. Так, сума |
і добуток двох |
неперервних |
в |
області |
D |
функцій |
|
комплексної змінної |
f1 z і |
f2 z є |
неперервними |
в |
області |
D; |
функція |
24

z |
f1 |
z |
|
є неперервною в тих точках області D, де f2 z 0; суперпозиція |
|
f2 |
z |
||||
|
функцій комплексної змінної w f z ; g w f z є |
||||
неперервних |
|||||
неперервною.
Розглянемо питання про існування і неперервність оберненої функції.
Означення 3. |
Неперервна однозначна функція комплексної змінної w f z |
||
|
називається однолистою в області D C, якщо для всіх різних |
||
|
точок z1 z2 , |
z1 D, z2 D, |
f z1 f z2 . |
Твердження: Якщо w f z |
однолиста в D і відображає область D в область |
||
E, то в області E існує обернена функція z f 1 w для всіх z D і для всіх |
|||
w f z E, |
тобто відображення, що здійснюється однолистою функцією є |
||
взаємно однозначним, і тому функція, обернена до однолистої, є однозначною.
Теорема Вейєрштрасса. Якщо функція комплексної змінної неперервна на
|
|
|
|
|
компактній множині, то вона обмежена, а її модуль досягає своїх |
|||
|
|
|
|
|
найбільшого і найменшого значень. |
|
||
Доведення. ► Нехай функція w f z є неперервною для |
z C. |
|||||||
|
|
|
|
|
|
|
t x, y є дійсною неперервною функцією двох |
|
Функція |
|
f |
|
|
|
u2 x, y v2 x, y |
||
|
|
|||||||
змінних, для якої справедлива, відома з курсу математичного аналізу, теорема, яка говорить про обмеженість функції f t x, y та її екстремум у замкненій
області. ◄
Означення 4. Функцію комплексної змінної w f z називають неперервною
на |
кривій z z t , t , , якщо неперервними на |
, |
є |
||||
функції u t Rew z t і v t Imw z t . (Якщо крива |
z z t |
є |
|||||
замкненою, то z z ). |
|
|
|||||
|
|
Розглянемо обмежену замкнену область |
D, межа |
||||
|
|
якої 1 2 ... n. В області D визначена |
|||||
|
|
неперервна функція w f z u x,y iv x,y , тобто |
|||||
1 |
n |
функції u x, y та v x, y є неперервними в областіD. |
|||||
Нехай функції u x,y та v x, y можна доозначити на |
|||||||
|
|
межі |
так, щоб отримати функції, неперервні у замк- |
||||
|
неній |
області |
|
. У такому випадку говорять, що |
|||
|
|
D |
|||||
|
|
функція комплексної змінної w f z є визначеною |
|
||||
для z D і неперервною в D, а також неперервною в області D аж до її межі.
25

Приклад 2. Нехай D z 2, Imz 0 . Дослідити на неперервність функцію
|
|
|
f z |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
z |
|
|
|
|
e |
|
2 , 0 в області |
D |
. |
|
|
|
|
|
||||||||||
|
• |
Маємо |
u x, y Re f z |
|
cos |
|
, |
v x, y Im f z |
|
sin |
|
, |
де |
||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
||||||
|
x2 |
y2 |
, |
arctg |
. Ці функції є неперервними всюди в області D, |
а це |
|||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
означає, |
що функція |
|
f z |
|
|
є неперервною в D. Довизначимо функцію |
|||||||||||||||||||||
|
|
z |
|||||||||||||||||||||||||
f z 
 z на межі області D:
z на межі області D:
f z f ei |
|
|
|
ei |
2 |
|
для |
2, 0 (на півкрузі); |
|||||||||
2 |
|||||||||||||||||
f z f ei |
|
|
|
|
|
|
|
для |
0 x 2, 0 |
|
x ; |
||||||
x |
|
||||||||||||||||
f z f ei i |
|
|
|
|
|
|
для |
2 x 0, |
|
|
x |
|
. |
||||
|
|
x |
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже, функція |
f z |
|
z |
|
є неперервною в області D. • |
||||||||
Приклад 3. |
Нехай D – круг |
|
z |
|
2 з розрізом вздовж відрізка 0, 2 . Дослідити |
||||||||
|
|
||||||||||||
|
f z |
|
|
|
|
|
i |
||||||
функцію |
|
|
|
|
|
e |
|
2 , де 0 2 , z ei на неперервність в |
|
. |
|||
|
z |
|
|
|
D |
||||||||
• У всіх точках області D функція f z 
 z є неперервною (приклад 2).
z є неперервною (приклад 2).
Im z
1
Rez
2
O 3 2
|
|
|
|
|
|
|
|
Довизначимо функцію |
f z z на межі |
||||||
області D: |
|
|
|
|
i |
||
|
|
|
f z |
|
|
|
|
: |
z |
2, 0 2 : |
2 |
e 2 ; |
|||
1 |
|
|
|
|
|
|
|
2:y 0, 0, 0 x 2 z x i 0 :
f z f x i 0 lim |
f z |
x |
; |
z x |
|
|
|
Imz 0
3: y 0, 2 ,0 x 2 z x i 0 :
f z f x i 0 |
lim f z |
x |
. |
|
z x |
||
|
Imz 0 |
||
Отже, функція f z 
 z не є неперервною в області D, оскільки на різних берегах розрізу функція набуває різних значень: її не можна "склеїти" так, щоб вона була неперервною вздовж розрізу. У цьому випадку функція f z
z не є неперервною в області D, оскільки на різних берегах розрізу функція набуває різних значень: її не можна "склеїти" так, щоб вона була неперервною вздовж розрізу. У цьому випадку функція f z 
 z є неперервною в області D аж до її межі. •
z є неперервною в області D аж до її межі. •
Означення 5. Функцію комплексної змінної w f z називають рівномірно неперервною в області D C, якщо
0 0: z1,z2 D: z1 z2 f z1 f z2 .
26

Якщо функція комплексної змінної є неперервною на компактній множині D, то на цій множині вона є рівномірно неперервною (теорема Кантора).
Розглянемо багатозначну функцію комплексної змінної w f z w n
 z; w Argz argz 2 k, k N, тощо). З геометричної точки зору, багатозначні функції не можна трактувати як відображення однієї області на іншу. За додаткових умов такі функції можна розглядати як однозначні функції, визначені не на комплексній площині, а на деякій гладкій поверхні, яку називають рімановою поверхнею, тобто як відображення областей на більш складних образах – ріманових поверхнях.
z; w Argz argz 2 k, k N, тощо). З геометричної точки зору, багатозначні функції не можна трактувати як відображення однієї області на іншу. За додаткових умов такі функції можна розглядати як однозначні функції, визначені не на комплексній площині, а на деякій гладкій поверхні, яку називають рімановою поверхнею, тобто як відображення областей на більш складних образах – ріманових поверхнях.
Простішим методом дослідження багатозначних функцій є виділення
окремих гілок таких функцій. |
|
D функція f1 z називається |
|
Означення. Однозначна і неперервна в області |
|||
однозначною і неперервною гілкою багатозначної функції f z , |
|||
якщо значення |
f1 z в кожній точці z D співпадає з одним із |
||
значень функції |
f z в цій точці. |
w f z |
|
Якщо для заданої багатозначної функції |
існує хоча б одна |
||
однозначна і неперервна гілка у заданій області |
D, то говорять, що функція |
||
f z допускає виділення однозначних і неперервних гілок в області D. |
|||
Розглянемо функцію w Argz arg z 2 k, k N , яка є визначеною на |
|||
всій комплексній площині C, |
за виключенням точок z 0 |
і z . Виділимо |
|
одну гілку цієї функції – головне значення w argz, тобто |
0 Argz 2 . Така |
||
однозначна гілка argz є визначеною для всіх z, |
за виключенням точок z 0 і |
||
z , а додатна дійсна піввісь 0 x , y 0 є для неї лінією розриву. Вилучимо з області визначення функції w argz точки додатної дійсної півосі.
Тоді функція w argz в області D C \ 0 Rez , Imz 0 є неперервною і
однозначною (однолистою) гілкою багатозначної функції |
|
|
w Argz. |
У такій |
||||||||||||||||||||||||||||||||||||||||||||||||||
області функція w argz є неперервною. |
Kr z0 z : |
|
|
|
|
|
|
|
|
|
r – круг, який |
|||||||||||||||||||||||||||||||||||||||||||
Зафіксуємо |
точку |
z0 D. Нехай |
|
z z0 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
лежить в D і не перетинається з віссю Im z 0, Rez 0. Тоді для z Kr |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
argz argz0 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
z z0 |
|
2 |
|
|
z |
|
2 |
|
|
z0 |
|
2 |
|
|
|
z |
|
|
|
z0 |
|
|
|
2 |
|
|
|
z z0 |
|
2 |
|
z |
|
2 |
|
z0 |
|
2 |
|
|||||||||||||
Оскільки |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
cos , то cos |
|
|
|
|
|
|
1. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
z |
|
|
|
z0 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z z0 |
|||||||||||||||
Це означає, |
|
що |
0 при |
|
z z0, що говорить |
|
|
про неперервність |
||||||||||||||||||||||||||||||||||||||||||||||
головної гілки функції w Argz. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
27

§ 4. Основні елементарні функції комплексної змінної
1. Лінійна функція: w az b, |
a,b C, |
a 0. |
Область визначення функції: |
D: z C. |
Якщо покласти w , то |
область визначення можна поширити на розширену комплексну площину C. Область значень : E : w C w , w C .
Знайдемо
|
Rew x Rea Reb y Ima, |
Im w y Rea Imb x Ima. |
|||||||||||||||||||
Ці |
функції є |
неперервними |
для x, y, |
|
що |
означає, |
що функція |
||||||||||||||
комплексної змінної w az b є неперервною на всій комплексній площині. |
|||||||||||||||||||||
Функція w az b є однолистою: якщо z1 |
z2 |
az1 b az2 b |
|||||||||||||||||||
w1 w2 . Це означає, що відображення |
D E є взаємно однозначним, а тому |
||||||||||||||||||||
існує функція, обернена до лінійної: |
|
|
w b |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
z f 1 w |
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
Розглянемо функцію |
|
|
|
|
a |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
w1 az |
|
a |
|
|
|
z |
|
cos arga argz i sin arga argz . |
|
|||||||||||
|
|
|
|
|
|
||||||||||||||||
Відображення w1 az кожному комплексному числу z |
ставить у відповідність |
||||||||||||||||||||
комплексне число az, модуль якого більший в |
|
a |
|
|
раз, а аргумент дорівнює сумі |
||||||||||||||||
|
|
||||||||||||||||||||
argz і |
постійного |
доданка arga. |
Геометричний зміст цього |
перетворення |
|||||||||||||||||
очевидний: розтяг площини z в a раз і поворот цієї площини як цілого навколо точки z 0 на кут arga.
Оскільки w w1 b, то перетворення w az b означає зсув площини az на вектор b.
Отже, лінійна функція w az b відображає комплексну площину z на комплексну площину w шляхом розтягу, повороту і зсуву.
2. Степенева функція w zn, n 2,3, .
Область визначення цієї функції: D: z C.
Область значень : E : w C w , w C .
Функція w zn є неперервною на всій комплексній площині C. Справді, |
|||||||
для z C, z C, |
|
z |
|
приріст w z z n z n n z zn 1 ... 0 для |
|||
|
|
||||||
z 0. |
w zn не є однолистою, оскільки, якщо покласти z ei , то |
||||||
Функція |
|||||||
w n ein , |
тобто |
|
|
w |
|
n, argw nargz. Це означає, що промені argz, які |
|
|
|
|
|||||
виходять з точки z 0, відображаються на промені argw nargz, які виходять з точки w 0, а точки комплексної площини z, модулі яких однакові, а аргументи
28

відрізняються на 2 (і тільки такі точки), відображаються в одну точку n
площини w. Отже, для однолистості відображення |
w zn |
в деякій області |
|||||||||||||||||||||||
D C, |
необхідно і достатньо, щоб область |
D не |
містила |
точок |
z1 і z2, |
||||||||||||||||||||
пов’язаних співвідношеннями |
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
z |
|
|
|
z |
|
|
, |
argz argz |
|
|
k, k Z . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
|
|
|
|
|
2 |
|
|
1 |
|
2 |
|
|
n |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Такій умові відповідають сектори |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
k argz |
2 |
k 1, |
k |
|
. |
|
|
|||||||||||||
|
|
|
|
0,n 1 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||||
Функція |
w zn обидві межі |
такого сектора відображає на промінь |
argw 0, |
||||||||||||||||||||||
який виходить з точки w 0 і йде у додатному напрямку дійсної осі площини w, всі внутрішні точки цього сектора взаємно однозначно відображає на всю
комплексну площину w вилученим променем argw 0 |
(з вирізаною піввіссю |
|||||||||
0 Rew , Imw 0). Це означає, що областю однолистості функції w zn |
є |
|||||||||
область D z C, |
0 argz 2 n , яку відображення |
w zn переводить в |
||||||||
область E w C\ Imz 0, 0 Rez . |
|
|
|
|
|
|||||
3. Функція w n |
|
, |
n N . |
|
|
|
|
|
||
z |
|
|
|
|
|
|||||
Функція w n |
|
є оберненою до функції w zn . |
|
|
|
|
|
|||
z |
|
|
|
|
|
|||||
Область визначення: D: z C. |
|
|
|
|
|
|||||
Область значень : E : w C. |
|
|
|
|
|
|||||
За теоремою про неперервність оберненої функції |
функція w n |
|
|
є |
||||||
z |
||||||||||
неперервною в області, |
в якій обернена функція w zn |
є неперервною |
та |
|||||||
однолистою. Такою областю є область D z C \ Imz 0, 0 Rez , яку
відображення w n |
|
переводить в сектор |
2 |
k argw |
2 |
k 1 . Точки z 0 і |
|||
z |
|||||||||
|
|
||||||||
|
|
|
n |
|
n |
||||
z є точками галуження для функції |
w n |
|
(в цих точках багатозначна |
||||||
z |
|||||||||
функція w n
 z набуває лише одного значення).
z набуває лише одного значення).
Побудова функції w zn дозволяє ввести в розгляд:
а) многочлени натурального степеня – цілі раціональні функції:
k
Pk z cmzm ,
m 0
б) дробово-раціональні функції – відношення двох многочленів:
R z Pm z . Qn z
29
Зрозуміло, що дробово-раціональна функція R z є визначеною та одно-
значною на всій комплексній площині C, за виключенням точок zk , в яких знаменник перетворюється в нуль. Ці точки називають особливими. Раціональна функція є неперервною всюди в області свого визначення.
4. Показникова функція w ez.
Область визначення цієї функції: D: z C.
Область значень : E : w C.
Показникову функцію комплексної змінної визначимо так: w ez ex iy ex cos y isin y .
Так визначена показникова функція задовольняє основній властивості показникової функції (теоремі додавання)
ez1 z2 ez1 ez2 ,
в чому легко переконатися, використовуючи означення. Справді, покладемо z1 x1 iy1, z2 x2 iy2. Тоді
ez1 ez2 ex1 ex2 cos y1 isin y1 cos y2 isin y2
ex1 x2 cos y1 cos y2 sin y1 sin y2 i sin y1 cos y2 cos y1 sin y2
ex1 x2 cos y1 y2 isin y1 y2 ez1 z2 .
Дійсна Rew ex cos y |
та уявна |
Imw ex sin y частини |
показникової |
|
функції w ez |
визначені і |
неперервні |
для x,y R2. Тому |
показникова |
функція w ez |
є неперервною на всій комплексній площині. |
|
||
Особливістю показникової функції комплексної змінної є періодичність. Використовуючи означення показникової функції, знайдемо для k Z
ez i2 k ex i y 2 k ex cos y 2 k isin y 2 k ex cos y isin y ez.
Отже, показникова функція є періодичною функцією з уявним періодом 2 i.
Знайдемо область однолистості. Нехай |
ez1 ez2 , де z |
x |
iy , |
z2 x2 iy2. Тоді |
1 |
1 |
1 |
|
|
|
|
|
x |
x |
2 |
|
cos y1 |
cos y2 . |
|
|
|
|
|
1 |
|
|
sin y1 |
sin y2 |
|
|
||
|
|
|
|
|
|
|
|
|||
Це означає, що |
x1 x2 і |
y1 |
y2 |
2 k, k Z . |
Тому |
областю |
однолистості |
|||
функції |
w ez |
є будь-яка смуга |
шириною 2 , |
сторони якої паралельні до |
||||||
дійсної осі, наприклад, область D z C, |
0 Imz 2 . Цю область відобра- |
|||||||||
ження |
w ez |
переводить |
у |
всю комплексну |
площину |
з розрізом |
||||
C\ Imw 0, 0 Rew (див. рис.). |
|
|
|
|
||||||
30
