
Конспект ТФКЗ
.pdfПриклад. Розвинути функцію f z |
|
1 |
|
|
в ряд Лорана в околі точки z . |
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 z4 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
||||||||||
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|||||||||||||
• Покладемо |
z |
|
: |
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
. Роз- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
|
4 1 |
1 4 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
винемо функцію в ряд Лорана в околі точки 0: |
|
|
|||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4 |
|
4 1 n 4n 1 n 1 4n, 0 |
|
|
|
1. |
|
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
1 4 |
|
n 0 |
|
|
n 1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Повертаючись в отриманому розвиненні до змінної z |
, маємо |
|
|
||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
f z |
|
1 n 1z 4n, |
|
1 |
|
z |
|
. • |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
4 |
|
|
|
||||||||||||||||||||||||||
|
|
|
1 z |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
91

ЛЕКЦІЯ 7
Теорія лишків та її застосування
§ 1. Класифікація та дослідження особливих точок однозначної аналітичної функції
Означення 1. Особлива точка z0 аналітичної функції w f z називається
ізольованою особливою точкою однозначного характеру функції f z ,
якщо в деякому її околі не має інших особливих точок функції f z . Лема 1 (про усувну особливість). Нехай функція w f z неперервна в об-
ласті D і аналітична в області D, за виключенням точок кривої D. Тоді функція f z є аналітичною і в точках кривої , тобто у всій області D.
Зауважимо, що крива , зокрема, може бути і однією точкою z D.
Означення 2. Ізольована особлива точка z0 однозначного характеру функції
fz називається:
1)усувною особливою точкою, якщо існує скінчена границя lim f z ;
2) |
полюсом, якщо lim f z ; |
z z0 |
|
|
|
||
|
z z0 |
|
|
3) |
істотно особливою точкою, якщо lim f z не існує. |
|
|
|
|
z z0 |
|
|
Усувна особлива точка |
f z . Тоді (і |
|
Нехай точка z0 є усувною особливою точкою функції |
|||
надалі) вважатимемо, що f z0 lim |
f z . Відповідно до леми 1 |
функція f z |
|
|
z z0 |
|
|
є аналітичною в точці z0, тобто в крузі z z0 R. Тому усувну особливу точку називають також неособливою, тобто аналітичною.
Приклад 1. Визначити характер особливої точки z0 |
0 функції f z |
sin z |
. |
|||||||
|
||||||||||
|
|
|
|
z2 |
|
|
z4 |
|
z |
|
• Для z 0 функція f z |
sin z |
1 |
|
. Ця функція є аналі- |
||||||
|
|
|
||||||||
|
z |
3! |
|
5! |
|
|
|
|||
тичною в точці z0 0 і f 0 1. Отже, |
z0 0 |
є усувною особливою точкою |
||||||||
функції |
f z |
sin z |
. • |
|
|
|
|
|
|
|
|||
|
|
z |
|
|
f z . Тоді (і |
|
Нехай точка z0 є усувною особливою точкою функції |
||||||
надалі) |
вважатимемо, що f lim |
f z , і точку |
z0 будемо також нази- |
|||
|
|
|
z |
|
|
|
вати неособливою, тобто аналітичною.
92
Означення 3. Точка z називається аналітичною точкою функції f |
z , якщо |
|||||||||||||||||||||||||||||
функція |
f z |
є аналітичною в |
кільці |
R |
|
z |
|
і |
існує |
скінчена |
||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
границя |
lim f z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||
Приклад 2. Визначити характер особливої точки z0 функції |
f z sin |
. |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
z |
||||
• У кільці |
0 |
|
z |
|
функція |
f z sin |
|
|
|
|
є аналітичною і |
|||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
3!z3 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
z |
|
|
|
|
|
|
|
|
|||||||
lim f z 0. Отже, z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
є усувною особливою точкою функції f z , тобто |
||||||||||||||||||||||||||||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аналітичною точкою. • |
|
|
|
|
|
Полюс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f z . Тоді існує таке число |
||||||||||||||||||
Лема 2. Нехай точка |
z0 є полюсом функції |
|||||||||||||||||||||||||||||
n N , що |
|
|
|
|
|
g z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
f z |
|
, g z0 0, |
|
|
(1.1) |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
z z0 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
де g z – аналітична в точці z0 функція. Число n називається |
||||||||||||||||||||||||||||||
порядком або кратністю полюса z0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Щоб знайти порядок полюса функції f z |
в точці |
z0, необхідно визна- |
||||||||||||||||||||||||||||
чити кратність нуля функції |
|
1 |
|
в точці |
z0 і подати функцію |
f z |
у вигляді |
|||||||||||||||||||||||
f |
z |
|||||||||||||||||||||||||||||
(1.1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
Приклад 3. Визначити порядок полюса z0 |
0 функції |
|
f z |
|
. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 cosz |
|
|
|
||||
• Визначимо кратність нуля функції 1 f z 1 cosz в точці z0 0. Розвинемо функцію 1
f z 1 cosz в точці z0 0. Розвинемо функцію 1 f z в ряд за степенями z:
f z в ряд за степенями z:
1 |
|
|
|
|
z2n |
|
|
z2 |
|
z4 |
|
|
|
|
z6 |
|
|
|
|
|
|
|
1 z2 |
|
z4 |
||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
f z |
1 1 |
|
|
1 |
1 |
2! |
|
|
|
|
|
|
z |
|
|
2! |
|
|
|||||||||||||||
|
n 0 |
|
2n ! |
|
|
4! |
6! |
|
|
|
|
|
|
|
4! |
6! |
|||||||||||||||||
Отже, |
f z |
1 |
|
|
g z |
|
, g z |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
, |
|
g 0 |
0 |
|||||||
1 cosz |
z2 |
|
1 |
|
|
|
z2 |
|
z |
4 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
4! |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6! |
|
|
|
|
|
|
|
|
|
|
||||||||
.
іточка
z0 0 є нулем функції |
g1 z 1 cosz кратності 2 і полюсом функції |
f z |
порядку 2. • |
|
|
Приклад 4. Визначити порядок полюса z0 2 функції |
f z |
z 2 2ez |
|
|
. |
||
|
|||
|
|
z 2 5 cosz |
|
93
• Оскільки функції ez,cosz аналітичні в точці z0 2 і e2 |
0,cos2 0, то |
||||||||||||||||||||||||||||||||||||||||||
функція g z |
ez |
є аналітичною в точці z0 |
2 |
і g 2 0. Для будь-якого z |
з |
||||||||||||||||||||||||||||||||||||||
cosz |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g z |
|
|
|
|
|
|
|
|
|
|
||||||
проколеного околу точки |
|
|
z0 2 |
маємо, |
що |
|
f z |
|
. |
Отже, z0 2 |
– |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f z . • |
|
|
|
|
|
z 2 3 |
|
|
|
|
|
|
|
|
||||||||||||
полюс третього порядку функції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Нехай точка |
z є полюсом функції |
f z , тобто функція f z |
є ана- |
||||||||||||||||||||||||||||||||||||||||
літичною в кільці R |
|
z |
|
, R 0 |
|
|
lim |
f z . Тоді функція g |
|
1 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
і |
f |
|
|
є |
|||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
аналітичною в кільці 0 |
|
|
|
|
|
і |
lim g , |
тобто 0 є полюсом функції |
|||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
R |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
g |
h |
|
h 0 0, де h |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
g . Тому існує таке натуральне число n, що |
, |
– |
|||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
аналітична в точці 0 функція. Тоді |
f z g |
|
|
znh |
|
|
, тобто |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f z znh z , |
|
z |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h 0, |
|
|
|
|
|
|
|
|
(1.2) |
|
|
|
|||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
де функція h1 z h |
|
|
|
– аналітична в |
точці |
z . Число |
n називається |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
z |
|
f z в точці z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
порядком полюса функції |
|
|
|
f z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Отже, щоб знайти порядок полюса функції |
в точці z , необхідно |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
1 |
|
|
0 |
і подати функцію f z |
|
||||||||||||||||||||
знайти порядок полюса функції |
|
|
в точці |
у |
|||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
вигляді (1.2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
Приклад 5. Визначити порядок полюса z0 функції f z |
|
. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
• Покладемо |
z |
|
і g |
|
. Точка |
0 |
є полюсом 1-го порядку |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
sin
функції g . Отже, z0 – полюс 1-го порядку функції f z . •
Приклад 6. Показати, що |
z0 є істотно особливою точкою функцій ez та |
|||||
sinz. |
|
|
|
|
|
|
• Обидві функції є аналітичними в області |
|
z |
|
. Але їх границі при |
||
|
|
|||||
z не існують ( lim ex |
, lim |
ex 0; lim sinx не існує). • |
||||
x |
x |
x |
||||
94
Зауваження. Якщо точка z0 є полюсом функції f z , то ця точка є істотно особливою для функції e f z .
Дослідження особливих точок часто зручно проводити, замінивши дану функцію більш простою еквівалентною функцією.
Означення 4. Функції f z і g z називаються еквівалентними при |
z z0, |
||||||||||
якщо вони аналітичні у проколеному околі точки z |
0 |
і |
lim |
|
f z |
1. |
|||||
|
|
|
|||||||||
У цьому випадку записують: f z ~g z для z z0. |
|
|
|
z z0 g z |
|
||||||
g z |
|
|
|
|
|
|
|
||||
Наприклад, з формули (1.1) випливає, що |
f z ~ |
|
для z z0. |
|
|||||||
z z0 n |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
Приклад 7. Визначити особливі точки функції |
f z |
1 cosz |
|
|
|
|
|
|
|
||
|
. |
|
|
|
|
|
|
||||
ez 13 |
|
|
|
|
|
|
|||||
• Особливими точками функції є точки, в яких дана функція не визначена і тому не аналітична, тобто точки, в яких знаменник функції f z дорівнює нулю.
Розв’язавши |
|
рівняння ez 1 0, |
знаходимо, що zk 2 ki, k Z . |
Крім того, |
|||||||||||||||||||||
точка z також є особливою точкою, оскільки значення |
|
f не визначене. |
|||||||||||||||||||||||
Кожна |
|
з |
точок |
zk |
2 ki, k Z |
|
є |
ізольованою |
|
особливою |
точкою |
||||||||||||||
однозначного характеру, |
тому що існує проколений окіл точки zk , |
в якому |
|||||||||||||||||||||||
функція |
f z є |
аналітичною. |
Точка |
z є точкою накопичення точок zk , |
|||||||||||||||||||||
оскільки |
lim zk |
. Дослідимо характер точок zk . |
|
|
|
|
|||||||||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
z 0. При z 0 маємо: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
z2 |
|
z |
2 |
|
|
|
z2 |
|
|
|
z |
|
|
|
|||
z 1 cosz |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
1 |
|
|
|
|
~ |
|
|
; |
ez 1 z 1 |
|
~z; |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
12 |
|
|
2 |
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
z ez 13~z3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Отже, f z ~ |
|
z2 |
|
1 |
, тобто точка z 0 – полюс 1-го порядку функції |
f z . |
|||||||||||||||||||
2z3 |
|
||||||||||||||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
zk 0, а zk |
|
|
|
|
|||||||
2) |
zk 2 ki, k Z, k 0. Оскільки |
|
|
– нуль кратності 3 |
|||||||||||||||||||||
|
|
|
ki, k 0 – полюси 3-го порядку функції |
f z . |
|||||||||||||||||||||
функції z , то точки zk 2 |
|||||||||||||||||||||||||
3) |
z . |
Довільний |
проколений |
окіл точки z |
містить |
ізольовані |
|||||||||||||||||||
|
|
|
f z |
|
|
zk, k Z а тому |
z – неізольована |
||||||||||||||||||
особливі точки функції |
– полюси |
|
|||||||||||||||||||||||
особлива точка функції f z . • |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Дослідження особливих точок за допомогою рядів Лорана
95

Якщо точка z0 є ізольованою особливою точкою аналітичної фун-кції
|
f z , то існує таке число R 0, |
що в кільці |
|
0 |
z z0 |
R функція f z буде |
||||||||||||||||||||||||||||||||||||||||||||
аналітичною і в цьому кільці функцію |
|
|
|
f z |
|
|
|
|
можна розвинути у ряд Лорана. |
|||||||||||||||||||||||||||||||||||||||||
Якщо z0 є |
ізольованою особливою точкою, |
|
то функцію |
f z можна |
||||||||||||||||||||||||||||||||||||||||||||||
розвинути в ряд Лорана у кільці |
|
|
R |
|
z |
|
|
|
. |
При цьому значення |
f z0 може |
|||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
бути невизначеним або невідомим. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Теорема 1. Для того, |
щоб ізольована особлива точка z0 функції f z була |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
усувною, необхідно і достатньо, щоб всі коефіцієнти головної частини |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
її ряду Лорана дорівнювали нулю, тобто |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
cn z z0 n |
0 |
для 0 |
|
z z0 |
|
|
R, R 0. |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Доведення. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
► Достатність. Якщо головна частина ряду Лорана відсутня, то ряд |
|||||||||||||||||||||||||||||||||||||||||||||||
Лорана функції |
f z |
є її рядом Тейлора. Тому lim |
|
f z c0, |
тобто точка z0 є |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z z0 |
|
|
|||||||||
усувною ізольованою особливою точкою функції f z . |
f z , тобто існує |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Необхідність. Нехай z0 – усувна особлива точка функції |
|||||||||||||||||||||||||||||||||||||||||||||||
|
lim f z . Отже, |
в кільці |
|
0 |
|
z z0 |
|
|
|
|
|
R1 R функція f z є обме-женою: |
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
z z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
f z |
|
M . Оцінимо коефіцієнти cn |
ряду Лорана для R1: |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
cn |
|
|
|
|
|
|
|
f d |
|
|
|
1 |
|
|
|
|
M |
|
|
|
M |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
. |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
2 i |
z |
0 |
n 1 |
2 |
|
|
|
n 1 |
n |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f d |
|
|
|||||
Якщо n 0, то cn 0 |
при 0. Але інтеграл |
|
не залежить від |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
n 1 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
|
|||||||
|
, тому cn 0 для n 0. ◄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Отже, якщо функція |
f z |
аналітична і обмежена у проколеному околі |
|||||||||||||||||||||||||||||||||||||||||||||
точки z0, то z0 – усувна особлива точка функції f z . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Теорема 2. Для того, |
щоб ізольована особлива точка z0 була полюсом |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
функції |
|
f z , |
необхідно |
і |
достатньо, щоб головна |
частина її ряду |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
Лорана містила скінчену кількість членів. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
Доведення. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z z0 |
|
R, R 0 |
|
|
||||||||||||||||||||||
|
|
|
► Достатність. Нехай в кільці 0 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
f z |
|
c m |
|
|
|
|
c m 1 |
|
|
|
|
, де c m 0, m N . |
|
||||||||||||||||||||||||||||||||||
|
|
|
z z0 m |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
z z0 m 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Тоді
96

|
f z |
c m c m 1 z z0 |
|
|
g z |
, |
|
z z0 m |
z z0 m |
||||
|
|
|
|
|||
де функція g z |
аналітична в точці z0 і g z0 c m 0, |
тобто z0 – полюс |
||||
порядку m функції f z .
Необхідність. Нехай z0 – полюс порядку m функції f z , тобто в кільці
0 |
z z0 |
R |
|
g z |
|
|
|
|
||
|
|
f z |
, |
g z0 0 |
||||||
|
|
z z0 m |
||||||||
|
|
|
|
|
|
|
g z c0 c1 z z0 , де |
|||
де функція g z є аналітичною в точці |
z0. |
Тоді |
||||||||
c0 g z0 0 і тому |
c0 |
c1 |
|
|||||||
|
|
f z |
|
|||||||
|
|
|
|
|
|
.◄ |
||||
|
|
z z0 m |
z z0 m 1 |
|||||||
Наслідок. З теорем 1 і 2, згідно з принципом виключення третього, випливає, що для того, щоб точка z0 була істотно особливою точкою функції f z , необхідно і достатньо, щоб головна частина її ряду Лорана містила нескінченну кількість членів.
Приклад 8. За допомогою розвинення функції в ряд Лорана показати, що: 1) точка z 0 є істотно особливою для функції f z z2e1 z ;
z ;
2) точка z 1 є істотно особливою для функції |
|
f z cos |
z |
. |
|||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
• 1) Функція |
f z z2e1 z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 1 |
|||||||||||
є аналітичною в кільці 0 |
|
z |
|
, в якому |
|||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||
f z z2ez z2 |
|
|
|
|
z2 z |
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n 0n!zn |
|
|
2 n 1 n 2 !zn |
|
|
|
|
|
|
||||||||||||||||||
Головна частина ряду Лорана містить нескінченну кількість членів, від- |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f z z2e |
|
. |
|||||||||||||||||||||
мінних від нуля. Отже, z 0 – істотно особлива точка функції |
z |
||||||||||||||||||||||||||||||||||||
2) У кільці 0 |
|
z 1 |
|
маємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
f z cos |
|
|
z |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
cos 1 |
|
|
|
|
|
|
cos1 cos |
|
|
sin1 sin |
|
|
|
|
||||||||||||||||||||
|
|
|
|
z 1 |
|
|
|
z 1 |
|||||||||||||||||||||||||||||
|
z 1 |
|
|
|
|
|
|
|
|
|
|
|
|
z 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
1 n |
|
|
|
|
|
|
|
1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
cos1 |
|
|
|
|
|
|
|
|
|
|
|
sin1 |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||
|
2n ! z 1 2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
n 0 |
|
|
|
n 0 2n 1! z 1 2n 1 |
|
|
|
|
|
|
||||||||||||||||||||||||
Оскільки головна частина ряду містить нескінченну кількість членів, відмінних від нуля, то точка z 1 є істотно особливою точкою функції
f z cos z . • z 1
97
Теорема 3 (теорема Сохоцького). Нехай z0 – істотно особлива точка функції
|
|
|
|
|
f z , |
аналітичної |
в |
кільці |
|
0 |
z z0 |
R. |
Тоді |
для |
будь-якого |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
комплексного числа A (скінченого |
чи ні) |
існує така послідовність zn , |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
яка збігається до істотно особливої точки z0, що |
lim |
f zn A. |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Доведення. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
► Нехай z0 , A . Щоб довести теорему, достатньо показати, що в |
||||||||||||||||||||||||||||||||||||||||||||||||||
довільному достатньо малому крузі з центром в точці z0 |
існують точки, в яких |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
f z A |
|
, |
де – довільне задане додатне число. Припустимо протилежне, а |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
саме, що в деякому околі точки z0 |
немає точок, в яких значення функції f z є |
||||||||||||||||||||||||||||||||||||||||||||||||||||
близьким до значення A, тобто існують такі числа 0, 0, що |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f z A |
|
|
|
, |
|
0 |
|
z z0 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Побудуємо нову функцію g z |
|
|
|
1 |
|
|
, яка в кільці |
0 |
|
z z0 |
|
|
|
є аналі- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
тичною і обмеженою |
|
|
|
|
|
|
|
f |
z A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g z |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
z A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Тоді за теоремою 1 z0 |
є усувною точкою функції g z , тобто для цієї функції |
||||||||||||||||||||||||||||||||||||||||||||||||||||
існує скінчена границя |
lim g z c c . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
z z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Якщо |
lim g z c 0, |
то |
для |
|
функції |
f z A |
|
|
|
|
маємо, |
що |
||||||||||||||||||||||||||||||||||||||
|
|
|
g z |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
lim f z і точка z0 була би полюсом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
z z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Якщо |
lim g z c 0, |
|
то lim |
f z 1 |
, |
і функція |
f z , |
яка є обме- |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
z z0 |
|
|
|
|
|
|
z z0 |
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
женою в деякому околі точки |
z0, |
повинна би мати в |
точці |
z0 |
усувну |
||||||||||||||||||||||||||||||||||||||||||||||||
особливість. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Отримані |
протиріччя і |
|
|
доводять |
справедливість |
теореми для |
випадку |
|||||||||||||||||||||||||||||||||||||||||||
|
A . |
|
|
|
|
|
|
f z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Нехай A . Функція |
|
|
не може бути обмеженою в жодному околі |
|||||||||||||||||||||||||||||||||||||||||||||||
точки z0, оскільки якщо б вона була обмеженою, |
то точка z0 |
була би усувною |
|||||||||||||||||||||||||||||||||||||||||||||||||||
особливою точкою для функції |
f z . |
Це |
означає, що для n N |
в околі |
|||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
z z0 |
|
|
1 |
знайдеться така точка zn, в якій |
|
f zn |
|
|
1 |
. Отже, в околі істотно |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
особливої точки знайдеться така послідовність zn , яка збігається до |
z0, |
що |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
lim f zn A. ◄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
98

Зауважимо, що має місце теорема, обернена до теореми 3.
Теорема 4. Якщо для функції f z , аналітичної в околі своєї ізольованої особливої точки z0, для довільного заданого числа A (скінченого чи ні)
знайдеться така послідовність zn |
, що |
lim f zn A, то точка z0 є |
істотно особливою точкою функції |
f z . |
n |
|
§ 2. Лишок однозначної аналітичної функції. Формули обчислення лишків
Нехай точка z0 є ізольованою особливою точкою однозначного характеру функції f z . Тоді в кільці R1 z z0 R2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f z cn z z0 n , |
|
|
|
(2.1) |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
f d |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
cn |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
(2.2) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
2 i |
|
z |
0 |
n 1 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де коло : |
|
z z0 |
|
, R1 R2 орієнтоване проти годинникової стрілки. |
|
||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
Означення 1. Лишком функції f z |
|
в точці z0 |
|
називається коефіцієнт |
c 1 |
||||||||||||||||||||||||||||
|
|
ряду Лорана. Позначають лишок у вигляді |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Res f z ,z0 res |
|
|
f z c 1. |
|
(2.3) |
|
||||||||||||||||
З формул (2.2), (2.3) отримуємо, що |
z z0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
f d 2 i Res f z ,z0 . |
|
|
|
(2.4) |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Приклад 1. Знайти лишок функції f z z2e1 z |
|
в точці z 0. |
|
|
|||||||||||||||||||||||||||||
• У кільці 0 |
|
z |
|
ряд Лорана функції |
|
f z z2e1 z |
має вигляд |
|
|||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
||||||||||||||
|
|
f z z2ez z2 |
1 |
|
|
z2 |
z |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n 0n!zn |
|
|
|
|
|
|
|
|
2 |
|
|
n 1 n 2 !zn |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
z2 z |
1 |
|
1 |
|
1 |
|
|
|
, |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4!z2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3!z |
|
|
|
|
|
|
|
|
||||||||||
1
звідки c 1 1 1, Res z2ez ,0 1 . •
3! 6 6
Приклад 2. Знайти лишок функції f z zcos |
1 |
в точці z 1. |
|
z 1
99

• Для точок z , які задовольняють нерівність 0 z 1 , маємо
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
f z |
z 1 1 1 |
|
|
|
z 1 1 |
, |
|||||||||||
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 z 1 |
|
||||
|
|
|
|
|
|
|
|
|
2 z 1 |
|
|
|
|
|||||
|
|
1 |
|
|
1 |
|
|
|
|
1 |
. • |
|
|
|
|
|||
звідки c 1 |
|
|
, |
Res zcos |
|
|
,0 |
|
|
|
|
|
||||||
2 |
z 1 |
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Означення 2. Лишком функції |
f z |
у точці z0 називається коефіцієнт ряду |
||||||||||||||||
|
Лорана при |
1 |
, взятий з протилежним знаком: |
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
f z c 1. |
|
|
|
|
|
|
|
|
|
|
Res f z , res |
|
|
(2.5) |
|||||||||
|
Тоді |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|||
|
|
|
|
f d 2 i Res f z , . |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
(2.6) |
|||||||||
Зауваження. Якщо точка z0 є усувною, тобто аналітичною точкою функції f z , то з означення 1 випливає, що Res f z ,z0 0. Але, якщо точка z0 є аналітичною для функції f z , то лишок Res f z , може бути і відмінним від нуля. Наприклад, Res1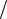 z, 1 0.
z, 1 0.
Обчислення лишку в полюсі z0 і в аналітичній точці z0 |
. |
|||||||||||||||||||||
Лема 1. Нехай точка z0 є полюсом порядку m функції |
f z . Тоді |
|
|
|||||||||||||||||||
Res f z ,z0 |
|
|
|
1 |
|
lim |
|
dm 1 |
z z0 m f z . |
(2.7) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
m 1!z z0 dzm 1 |
|
|
|
|
|
|
|
|||||||||||||
Зокрема, для m 1 з формули (2.7) маємо |
|
|
|
|
||||||||||||||||||
Res f z ,z0 lim z z0 f z . |
|
(2.8) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
z z0 |
|
|
|
|
|
|
|
|
||||||
Приклад 3. Знайти лишок функції |
|
f z |
1 |
sin z в точці z0 |
0. |
|
|
|||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
||
• Точка z0 0 – полюс першого порядку. Тому за формулою (2.8) |
|
|||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
sin z |
1. • |
|
|
|
||||
Res |
|
|
sin z,0 |
lim |
|
|
|
|
|
|
|
|||||||||||
|
|
|
z |
|
|
|
||||||||||||||||
|
z2 |
|
|
|
|
|
|
|
z 0 |
|
|
|
|
|
||||||||
Зауваження. Якщо f z |
h z |
, |
де функції |
h z , g z – |
аналітичні |
в точці |
||||||||||||||||
|
||||||||||||||||||||||
|
g z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
z0 і h z0 0, g z0 0, g z0 0, то |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Res f z ,z |
0 |
|
h z0 |
. |
|
|
(2.9) |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
g z0 |
|
|
|
|
||||||
100
