
Metod_labs_v5
.pdf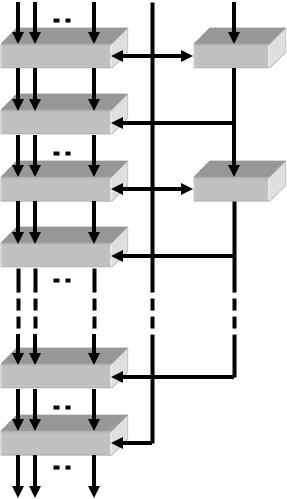
комутатори прямих зв’язків, за допомогою яких здійснюється налаштування КС на виконання необхідної операції. Відмінність структури багатофункціонального КОП від однофункціонального полягає в наявності конвеєрних регістрів команд КРК, що зберігають код операції, а також зв’язків для налаштування на потрібну операцію комбінаційних схем ярусів КОП. По конвеєру, під керуванням тактових імпульсів Т, синхронно з даними просуваються і команди по КРК. Команда з виходу відповідного регістра налаштовує комбінаційні схеми ярусу на виконання необхідної операції. Для ярусів конвеєра можна записати: Ai+1= Фі(Аі, Кі), де Кі – вмістиме регістра КРК і-го ярусу конвеєра На регістри ярусів конвеєра , що звільнюються, в кожному такті надсилаються нові дані оброблюваного масиву, над яким виконуються ті ж операції. Перетворення над вхідними даними Х в КОП описується виразом:
У=Фm+1 (Кm, Фm(. . . , Ф(К, Х). . . ))).
X1, X2,… Xn
КРД1 |
|
|
|
КРК1 |
|
|
|
|
|
КС1
КРД2 |
|
|
|
КРК2 |
|
|
|
|
|
КС2
КС m
Y1, YКРД2, …nYs
Рис. 2. Структура КОП.
БК здійснює загальну синхронізацію, адресацію БП, задає коди операцій КОП організовує цикли. В даній лабораторній роботі керуючі сигнали БК можна задавати як сигнали, що надходять ззовні, тобто сам БК не треба проектувати як окремий пристрій. Достатньо подати відповідні керуючі сигнали на КОП та БП.
Техніка конвеєризації може бути застосована до задач, що виконуються поетапно. Для ілюстрації цієї концепції розглянемо та імплементуємо функцію f = а*b + c.
Для перетворення прототипу комбінаційної схеми в потокову структуру та отримання VHDL коду цієї процедури, зручно використовувати такі кроки:
1)Створити блок-схему оригінальної комбінаційної схеми та організувати її компоненти в вигляді каскадної послідовності.
2)Визначити основні компоненти блок-схеми та оцінити відносні тривалості їх виконання.
3)Поділити послідовність компонентів на етапи так, щоб тривалість етапів була приблизно рівною.
4)Визначити дані й сигнали необхідні на кожному етапі опрацювання та вибрати ті, які надходять з інших етапів опрацювання.
5)Розмістити регістри для зберігання даних й сигналів, які находять з інших етапів опрацювання.
Заналізу 1-го та 2-го кроків видно, що розділивши виконання функції f на 1й: a*b та 2й: (a*b)+c кроки, поділити послідовність компонентів на етапи так, щоб тривалість етапів була приблизно рівною – важко, оскільки операція множення є затратнішою від сумування, а отже може вимагати більшого часу для виконання. Для вирішення цієї задачі доцільно або використовуючи схему помножувача на основі суматорів, виконати його декомпозицію і далі розглядати його компоненти як складові комбінаційної схеми, або розглядаючи помножувач як неподільний елемент виконати його оптимізацію.
Розглянемо другий варіант реалізації. Тому, виконаємо оптимізацію помножувача за часовим критерієм шляхом його конвеєризації використовуючи вищенаведену процедуру.
Розглянемо простий приклад перетворення схеми помножувача на основі суматорів (обговореного в лабораторній роботі № 2) в каскадну структуру.
Для зменшення громіздкості прикладу розглянемо процес конвеєризації 5ти бітного помножувача. Двома основними компонентами розглянутого помножувача є суматор і схема побітового множення. Для спрощення процесу розробки компоненти помножувача організовуються в каскад. Реорганізована блок схема зображена на рис. 3(а). AND – схема логічного множення, яка включає лише операції побітового логічного множення і доповнення нулями, а отже час її виконання є відносно малим. Тому для формування каскаду схему логічного множення об’єднуємо з суматором. На рис. 3(а) каскади розділені штриховими лініями, сигнали пронумеровані відповідно до номера сходинки каскаду. Для забезпечення потокового опрацювання, зберігання проміжних
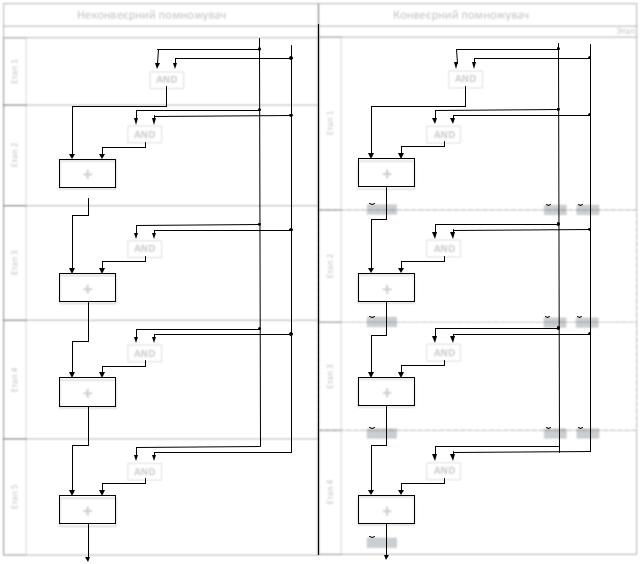
результатів(часткових добутків) та даних необхідних на кожній сходинці використовуються регістри. Так, отримуємо частково незалежні сходинки каскаду.
З розглянутої блок-схеми (рис.3) отримаємо відповідний VHDL код, наведений в лістингу нижче.
Етап 1
Етап 2
Етап 3
Етап 4
Етап 5
Неконвеєрний помножувач
AND pp0
AND
+  pp1
pp1
AND
+
pp2
AND
+
pp3
AND
+
pp4
y
a |
b |
|
|
a0 |
b0 |
Етап 1
a1 |
b1 |
Етап 2
a2 |
b2 |
Етап 3
a3 |
b3 |
Етап 4
Конвеєрний помножувач
Этап
a |
b |
|
AND pp0
AND
+ |
|
|
pp1 |
a1_next |
b1_next |
pp1_next |
||
pp1_reg |
a1_reg |
b1_reg |
|
AND |
|
+ |
|
|
pp2_next pp2 |
a2_next |
b2_next |
pp2_reg |
a2_reg |
b2_reg |
|
AND |
|
+ |
|
|
pp3_next |
a3_next |
b3_next |
pp3_reg |
a3_reg |
b3_reg |
|
||
|
AND |
|
+ |
|
|
pp4_next |
|
|
pp4_reg |
|
|
y |
|
|
(а) (б)
Рис. 3. Блок схема неконвеєрного (a) та 4х сходинкового конвеєрного (б) помножувачів
VHDL код 5-ти бітного неконвеєрного помножувача:
library IEEE;
use IEEE.STD_LOGIC_1164.ALL; use IEEE.NUMERIC_STD.ALL;
entity gvv_mult is
Port ( gvv_clk : in STD_LOGIC; gvv_reset : in STD_LOGIC;
gvv_a : in STD_LOGIC_VECTOR (4 downto 0);
gvv_b : in STD_LOGIC_VECTOR (4 downto 0); gvv_y : out STD_LOGIC_VECTOR (9 downto 0));
end gvv_mult;
architecture Behavioral of gvv_mult is constant WIDTH: integer:=5;
signal gvv_a0, gvv_a1, gvv_a2, gvv_a3 : std_logic_vector(WIDTH-1 downto 0);
signal gvv_b0, gvv_b1, gvv_b2, gvv_b3 : std_logic_vector(WIDTH-1 downto 0);
signal gvv_bv0, gvv_bv1, gvv_bv2, gvv_bv3, gvv_bv4 : std_logic_vector(WIDTH - 1 downto 0);
signal gvv_bp0, gvv_bp1, gvv_bp2, gvv_bp3, gvv_bp4 : unsigned(2*WIDTH - 1 downto 0);
signal gvv_pp0, gvv_pp1, gvv_pp2, gvv_pp3, gvv_pp4 : unsigned(2*WIDTH - 1 downto 0);
begin
-- stage 0
gvv_bv0 <= (others => gvv_b(0));
gvv_bp0 <= unsigned("00000" & (gvv_bv0 and gvv_a)); gvv_pp0 <= gvv_bp0;
gvv_a0 <= gvv_a; gvv_b0 <= gvv_b; -- stage 1
gvv_bv1 <= (others => gvv_b0(1));
gvv_bp1 <= unsigned("0000" & (gvv_bv1 and gvv_a0) & "0"); gvv_pp1 <= gvv_pp0 + gvv_bp1;
gvv_a1 <= gvv_a0; gvv_b1 <= gvv_b0; -- stage 2
gvv_bv2 <= (others => gvv_b1(2));
gvv_bp2 <= unsigned("000" & (gvv_bv2 and gvv_a1) & "00"); gvv_pp2 <= gvv_pp1 + gvv_bp2;
gvv_a2 <= gvv_a1; gvv_b2 <= gvv_b1; -- stage 3
gvv_bv3 <= (others => gvv_b2(3));
gvv_bp3 <= unsigned("00" & (gvv_bv3 and gvv_a2) & "000"); gvv_pp3 <= gvv_pp2 + gvv_bp3;
gvv_a3 <= gvv_a2; gvv_b3 <= gvv_b2; -- stage 4
gvv_bv4 <= (others => gvv_b3(4));
gvv_bp4 <= unsigned("0" & (gvv_bv4 and gvv_a3) & "0000"); gvv_pp4 <= gvv_pp3 + gvv_bp4;
-- result
gvv_y <= std_logic_vector(gvv_pp4); end Behavioral;
При приведенні схеми до потокового варіанту спочатку ділимо послідовність компонентів на етапи так, щоб тривалість етапів була приблизно рівною, та розміщуємо між ними регістри а слідом відповідно до них перекомутовуємо вхідні та вихідні сигнали. Тепер замість отримання даних із попередньої сходинки опрацювання, кожна сходинка конвеєра отримує їх із «граничного» регістра. Наприклад, сигнал gvv_pp2 непотокового перемножувача генерується на 2-му етапі, а потім використовується на 3-му.
-- stage 2
gvv_pp2 <= gvv_pp1 + gvv_bp2; -- stage 3
gvv_pp3 <= gvv_pp2 + gvv_bp3;
В потоковому варіанті сигнал повинен бути збережений в регістр.
-- pipeline registers process(gvv_clk,gvv_reset) begin
if (gvv_reset = '1') then
gvv_pp2_reg <= (others => '0'); elsif (gvv_clk'event and gvv_clk = '1') then
gvv_pp2_reg |
<= gvv_pp2_next; |
end if; |
|
VHDL код 5-ти бітного конвеєрного помножувача (відповідно до рис. 3(б)):
library IEEE;
use IEEE.STD_LOGIC_1164.ALL; use IEEE.NUMERIC_STD.ALL;
entity gvv_pipeline_mult is |
|
|
Port ( gvv_clk : in STD_LOGIC; |
|
|
gvv_reset : in STD_LOGIC; |
|
|
gvv_a : in |
STD_LOGIC_VECTOR (4 downto 0); |
|
gvv_b : in |
STD_LOGIC_VECTOR (4 downto 0); |
|
gvv_y : out |
STD_LOGIC_VECTOR (9 downto 0)); |
|
end gvv_pipeline_mult; |
|
|
architecture Behavioral of gvv_pipeline_mult is |
|
|
constant WIDTH: integer:=5; |
|
|
signal gvv_a1_reg, gvv_a2_reg, gvv_a3_reg : |
|
|
std_logic_vector(WIDTH-1 downto 0); |
|
|
signal gvv_a0, gvv_a1_next, gvv_a2_next, gvv_a3_next |
: |
|
std_logic_vector(WIDTH-1 downto 0); |
|
|
signal gvv_b1_reg, gvv_b2_reg, gvv_b3_reg : |
|
|
std_logic_vector(WIDTH-1 downto 0); |
|
|
signal gvv_b0, gvv_b1_next, gvv_b2_next, gvv_b3_next : |
|
|
std_logic_vector(WIDTH-1 downto 0); |
|
|
signal gvv_bv0, gvv_bv1, gvv_bv2, gvv_bv3, gvv_bv4 |
: |
|
std_logic_vector(WIDTH-1 downto 0); |
|
|
signal gvv_bp0, gvv_bp1, gvv_bp2, gvv_bp3, gvv_bp4 |
: |
|
unsigned(2*WIDTH - 1 downto 0);
signal gvv_pp1_reg, gvv_pp2_reg, gvv_pp3_reg, gvv_pp4_reg : unsigned(2*WIDTH - 1 downto 0);
signal gvv_pp0, gvv_pp1_next, gvv_pp2_next, gvv_pp3_next, gvv_pp4_next : unsigned(2*WIDTH - 1 downto 0);
begin
-- pipeline registers process(gvv_clk,gvv_reset) begin
if (gvv_reset = '1') then
gvv_pp1_reg |
<= (others => '0'); |
gvv_pp2_reg |
<= (others => '0'); |
gvv_pp3_reg |
<= (others => '0'); |
gvv_pp4_reg |
<= (others => '0'); |
gvv_a1_reg |
<= (others => '0'); |
gvv_a2_reg |
<= (others => '0'); |
gvv_a3_reg |
<= (others => '0'); |
gvv_b1_reg |
<= (others => '0'); |
gvv_b2_reg |
<= (others => '0'); |
gvv_b3_reg |
<= (others => '0'); |
elsif (gvv_clk'event and gvv_clk = '1') then
gvv_pp1_reg |
<= gvv_pp1_next; |
gvv_pp2_reg |
<= gvv_pp2_next; |
gvv_pp3_reg |
<= gvv_pp3_next; |
gvv_pp4_reg |
<= gvv_pp4_next; |
gvv_a1_reg |
<= gvv_a1_next; |
gvv_a2_reg |
<= gvv_a2_next; |
gvv_a3_reg |
<= gvv_a3_next; |
gvv_b1_reg |
<= gvv_b1_next; |
gvv_b2_reg |
<= gvv_b2_next; |
gvv_b3_reg |
<= gvv_b3_next; |
end if; end process;
-- stage 0 & 1 for pipeline gvv_bv0 <= (others => gvv_b(0));
gvv_bp0 <= unsigned("00000" & (gvv_bv0 and gvv_a)); gvv_pp0 <= gvv_bp0;
gvv_a0 <= gvv_a; gvv_b0 <= gvv_b;
gvv_bv1 <= (others => gvv_b0(1));
gvv_bp1 <= unsigned("0000" & (gvv_bv1 and gvv_a0) & "0"); gvv_pp1_next <= gvv_pp0 + gvv_bp1;
gvv_a1_next <= gvv_a0; gvv_b1_next <= gvv_b0; -- stage 2
gvv_bv2 <= (others => gvv_b1_reg(2));
gvv_bp2 <= unsigned("000" & (gvv_bv2 and gvv_a1_reg) & "00"); gvv_pp2_next <= gvv_pp1_reg + gvv_bp2;
gvv_a2_next <= gvv_a1_reg; gvv_b2_next <= gvv_b1_reg; -- stage 3
gvv_bv3 <= (others => gvv_b2_reg(3));

|
|
|
gvv_bp3 <= unsigned("00" & (gvv_bv3 and gvv_a2_reg) & "000"); |
||||||||||||||||||||||||||
|
|
|
gvv_pp3_next |
<= gvv_pp2_reg + gvv_bp3; |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
gvv_a3_next |
<= gvv_a2_reg; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
gvv_b3_next |
<= gvv_b2_reg; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
-- stage 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
gvv_bv4 <= (others => gvv_b3_reg(4)); |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
gvv_bp4 <= unsigned("0" & (gvv_bv4 and gvv_a3_reg) & "0000"); |
||||||||||||||||||||||||||
|
|
|
gvv_pp4_next <= gvv_pp3_reg + gvv_bp4; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
-- result |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
gvv_y <= std_logic_vector(gvv_pp4_reg); |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
end Behavioral; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AND |
AND |
AND |
|
AND |
AND |
AND |
AND |
AND |
AND |
AND |
|||||||||||||||||||
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
||||
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
||
Рис. 4 Блок-схема неконвеєрного (a) та 3х сходинкового конвеєрного (б) помножувачів з деревовидною структурою
Ефективність конвеєрного перемножувача можна підвищити шляхом використання суматорів меншої розрядності (n+1 біт) відповідно до підходу описаного у лабораторній роботі № 2.
В n-розрядних комбінаційних помножувачах критичний шлях включає n-1 каскадно розміщених суматорів. Цей критичний шлях (часова складність) може бути зменшений до log2N суматорів шляхом використання
VHDL код 5-ти бітного конвеєрного помножувача з деревовидною структурою (відповідно до рис. 4(б)):
library IEEE;
use IEEE.STD_LOGIC_1164.ALL; use IEEE.NUMERIC_STD.ALL;
entity gvv_tree_pipe_mult is
Port ( gvv_reset : in STD_LOGIC; gvv_clk : in STD_LOGIC;
gvv_a |
: in |
STD_LOGIC_VECTOR (4 downto 0); |
|
gvv_b |
: in |
STD_LOGIC_VECTOR (4 downto 0); |
|
gvv_y : out |
STD_LOGIC_VECTOR (9 downto 0)); |
|
|
end gvv_tree_pipe_mult; |
|
|
|
architecture tree_pipe_arch of gvv_tree_pipe_mult is |
|
||
constant WIDTH: integer:=5; |
|
||
signal gvv_bv0, gvv_bv1, gvv_bv2, gvv_bv3, gvv_bv4 |
: |
||
std_logic_vector(WIDTH - 1 downto 0); |
|
||
signal gvv_bp0, gvv_bp1, gvv_bp2, gvv_bp3, gvv_bp4 |
: |
||
unsigned(2*WIDTH - 1 downto 0); |
|
||
signal gvv_bp4_s1_reg, gvv_bp4_s2_reg |
|
||
:unsigned(2*WIDTH - 1 downto 0); signal gvv_bp4_s1_next, gvv_bp4_s2_next
:unsigned(2*WIDTH - 1 downto 0);
signal gvv_pp01_reg, gvv_pp23_reg, gvv_pp0123_reg,
gvv_pp01234_reg |
: unsigned(2*WIDTH - 1 downto 0); |
signal gvv_pp01_next, gvv_pp23_next, gvv_pp0123_next, |
|
gvv_pp01234_next |
: unsigned(2*WIDTH - 1 downto 0); |
begin |
|
-- pipeline registers process(gvv_clk,gvv_reset) begin
if (gvv_reset = '1') then
gvv_pp01_reg |
<= (others => '0'); |
gvv_pp23_reg |
<= (others => '0'); |
gvv_pp0123_reg |
<= (others => '0'); |
gvv_pp01234_reg |
<= (others => '0'); |
gvv_bp4_s1_reg |
<= (others => '0'); |
gvv_bp4_s2_reg |
<= (others => '0'); |
elsif (gvv_clk'event and gvv_clk = '1') then gvv_pp01_reg <= gvv_pp01_next; gvv_pp23_reg <= gvv_pp23_next; gvv_pp0123_reg <= gvv_pp0123_next; gvv_pp01234_reg <= gvv_pp01234_next; gvv_bp4_s1_reg <= gvv_bp4_s1_next; gvv_bp4_s2_reg <= gvv_bp4_s2_next;
end if; end process;
--stage 1 -- bit product -- gvv_bv0 <= (others => gvv_b(0));
gvv_bp0 <= unsigned("00000" & (gvv_bv0 and gvv_a)); gvv_bv1 <= (others => gvv_b(1));
gvv_bp1 <= unsigned("0000" & (gvv_bv1 and gvv_a) & "0"); gvv_bv2 <= (others => gvv_b(2));
gvv_bp2 <= unsigned("000" & (gvv_bv2 and gvv_a) & "00"); gvv_bv3 <= (others => gvv_b(3));
gvv_bp3 <= unsigned("00" & (gvv_bv3 and gvv_a) & "000"); gvv_bv4 <= (others => gvv_b(4));
gvv_bp4 <= unsigned("0" & (gvv_bv4 and gvv_a) & "0000"); -- adder
gvv_pp01_next <= gvv_bp0 + gvv_bp1; gvv_pp23_next <= gvv_bp2 + gvv_bp3; gvv_bp4_s1_next ,<= gvv_bp4;
-- stage 2
gvv_pp0123_next <= gvv_pp01_reg + gvv_pp23_reg; gvv_bp4_s2_next <= gvv_bp4_s1_reg;
-- stage 3
gvv_pp01234_next <= gvv_pp0123_reg + gvv_bp4_s2_reg;
gvv_y <= std_logic_vector(gvv_pp01234_reg); end tree_pipe_arch;
Далі виконануємо перевірку розроблених поведінкових моделей, синтез, імплементування, генерацію умовних графічних позначень розроблених компонентів. Проаналізуємо RTL та технологічні схеми. Виконаємо функціональне моделювання схеми шляхом створення тестового файлу, в якому декларуємо поведінку вхідних сигналів.
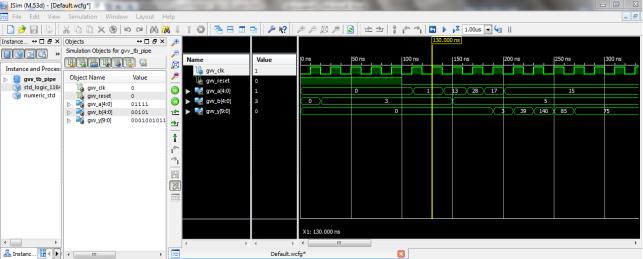
Результатом роботи є часові діаграми моделювання розроблених перемножувачів (рис.5,7,8).
Рис. 5 Часові діаграми моделювання конвеєрного перемножувача
Для зручності відлагодження та наочної демонстрації конвеєрного опрацювання у ISim симуляторі додаємо внутрішні сигнали у вікно симуляції
(рис. 6,7).
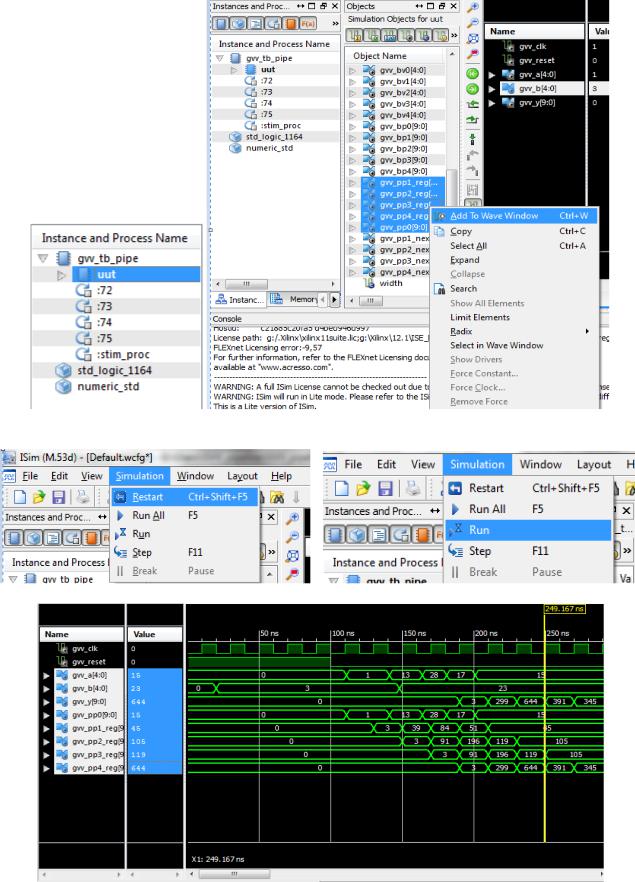
Рис.6 Фрагмент вікна ISim симулятора: додавання додаткових сигналів у вікно симуляції
Рис.7 Фрагмент вікна ISim симулятора: повторна генерація часових діаграм
Рис.8. Часові діаграми моделювання конвеєрного перемножувача з доданими об’єктами для перегляду внутрішніх сигналів
