2. Теорема Польке

Зобразимо на площині П чотирикутник АВСD з діагоналями АС та ВD, що перетинаються. Проведемо з кожної вершини чотирикутника паралельні прямі, що перетинають площину П і візьмемо на цих прямих довільні точки А,В,С,D, які не лежать в одній площині (рис. 17.2).

Чотирикутник АСВD можна розглядати, як паралельну проекцію тетраедра АВСD. Серед безлічі тетраедрів, прoекції яких відповідають чотирикутнику АВСD, є і такий, у якого три ребра АВ, АС і АD взаємно перпендикулярні і дорівнюють одне одному. Ці три ребра можуть бути прийняті за напрям осей декартової системи координат, на яких відкладені натуральні одиниці виміру. Тоді відрізки АВ, АС і АD можуть бути прийняті за аксонометричні осі координат, на яких відкладені аксонометричні масштаби.

Рис. 17.2

Теорема Польке: Будь-який чотирикутник зі своїми діагоналями може бути отриманий, як паралельна проекція деякої масштабної трикутної піраміди.

Теорема Польке-Шварца: Будь-який плоский чотирикутник зі своїми діагоналями може бути отриманий, як паралельна проекція деякої трикутної піраміди, яка подібна будь якій даній трикутній піраміді.

Наслідок з цих теорем: Три будь-яких відрізка довільної довжини, які виходять з одної точки на площині, можуть бути розглянуті як паралельна проекція трьох рівних відрізків, які відкладені на взаємно перпендикулярних осях проекцій у просторі.

17.3. Трикутник слідів і його властивості

Якщо взяти аксонометричну площину П так, щоб вона перетинала всі три координатні осі в точках X,Y,Z і способом прямокутного проектування спроектувати точку О на П (рис.17.3), то відрізок ОО буде перпендикулярним до П. Позначимо  OXO ; OYO ; OZO .

Відрізки ОX, OY, OZ є катетами прямокутних трикутників.

Відрізки O X, OY,OZ є гіпотенузами прямокутних трикутників.

З цих прямокутних трикутників можна записати:

ОХ ОХ = cos, ОY ОY = cos , OZ OZ = cos .

Або cos  = k, cos  = m, cos  = n.

Теорема. Сума квадратів показників спотворення в прямокутній аксонометрії дорівнює 2.

k+ m+ n= 2

В аналітичній геометрії при розгляданні куба, доводиться рівняння:

cos +cos +cos = 1.

Але cos = sin, cos = sin, cos = sin.

sin+sin+sin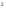 = 1,

1  cos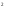  1  cos  1  cos = 1,

cos  cos  cos = 2,

або k+m+n= 2

Рис. 17.3

Площина аксонометричних проекцій П, перетинаючи площини координат, утворює трикутник XYZ, який називається трикутником слідів.

Властивості трикутника слідів.

1. Трикутник слідів завжди гострокутний.

2. В прямокутних аксонометричних проекціях аксонометричні осі є висотами трикутника слідів.

3. Три відрізка на площині, які виходять з однієї точки тільки в тому випадку є аксонометричними осями, якщо вони утворюють між собою тупі кути.

4. Прямокутні аксонометричні проекції

Прямокутна ізометрична проекція.

Якщо розмістити осі координат OX OY OZ під однаковими кутами до площини П, то cos = cos = cos і, відповідно, k = m = n, утвориться прямокутна ізометрія.

На основі вище розглянутої теореми 3k = 2,

звідки k = m = n = = 0,82.

Щоб побудувати предмет в ізометрії, треба всі його лінійні розміри, паралельні координатним осям, помножити на коефіцієнт спотворення 0,82. Таке зображення називається точним.

На практиці побудову ізометрії спрощують: відкладають по осях ОX, ОY, ОZ і паралельно їм натуральні розміри предмета, тобто коефіцієнт спотворення k = 0,82 замінюють на приведений коефіцієнт спотворення k = 1. Утворюється збільшене зображення без порушення пропорційності його елементів. Це збільшення становить 1 0,82  1,22 рази.

Осі в прямокутній ізометрії розміщуються під кутами 120 (при цьому вісь OZ - вертикально) (рис. 17.4).

Рис. 17.4 Рис. 17.5

Прямокутна диметрична проекція.

Якщо двом осям (найчастіше OX і OZ) задати рівний нахил до площини П, а третю вісь нахилити так, щоб показник спотворення по ній був удвічі меншим, ніж по двох інших осях  k = n, m = 0,5k, утвориться прямокутна диметрія.

Згідно формули k+ m+ n= 2маємо k = n = 0,94; m = 0,47.

За стандартом використовують так звану збільшену диметрію з коефіцієнтами k = n = 1 і m = 0,5. Величина збільшення при цьому становить 1,06.

Осі в прямокутній диметрії розміщуються так: вісь OZ - вертикально, а осі: OX і OY - під кутами 710 і 4125, відповідно, до горизонтального напрямку (рис. 17.5).