Запитання для самоперевірки

1. У яких випадках для визначення лінії перетину двох поверхонь можна використати спосіб концентричних сфер? ексцентричних сфер?

2. Які лінії одержують при взаємному перетині двох поверхонь обертання, описаних навколо спільної для них сфери або вписаних у сферу?

3. По яких лініях перетинаються між собою дві співвісні поверхні обертання?

4. Вкажіть способи, які використовуються для побудови проекцій лінії перетину поверхонь?

ЛЕКЦІЯ 16

РОЗГОРТКА ПОВЕРХОНЬ

16.1. Розгортка поверхонь. Основні властивості розгортки.

Види розгорток

Розгорткою поверхні називається плоска фігура, що утворюється при суміщенні поверхні з площиною. Поверхні, які не можуть бути суміщені з площиною, відносяться до нерозгортних поверхонь.

До групи розгортних поверхонь відносяться тільки лінійчаті поверхні і, зокрема ті з них, які мають пересічні суміжні твірні. Точка перетину може бути як власною (поверхні з ребром звороту і конічні), так і невласною (циліндричні поверхні).

Деякі геометричні властивості елементів поверхонь не змінюються при розгортці. Оскільки розгортка поверхні являє собою плоску фігуру, утворену з поверхні без розривів і склеювання, то кожній точці (фігурі) на поверхні відповідає точка (фігура) на розгортці і навпаки. Звідси випливають основні властивості розгортки поверхонь:

1. Довжини двох відповідних ліній поверхні та її розгортки рівні між собою, наслідком чого є те, що замкнена лінія на поверхні і відповідна їй лінія на розгортці обмежують однакову площу.

2. Кут між лініями на поверхні дорівнює куту між відповідними їм лініями на розгортці.

3. Прямій на поверхні відповідає також пряма на розгортці (зворотне твердження не має змісту).

4. Паралельним прямим на поверхні відповідають також паралельні прямі на розгортці.

В залежності від виду поверхонь їхні розгортки можуть бути: точними, наближеними і умовними.

Точна розгортка може бути побудована лише для многогранників та відсіків розгортних поверхонь (циліндра, конуса, торса) - поверхню многогранника завжди можна сумістити з площиною, тому що вона складається з плоских відсіків.

Побудова точної розгортки похилого конуса або циліндра пов’язана з обчисленням довжини кривої лінії, що само по собі ставить не просту задачу. Тому розгортку будують наближено, замінюючи поверхню конуса многогранною пірамідою, а поверхню циліндра поверхнею многогранної призми.

При побудові розгортки нерозгортних поверхонь (сфера, тор) їх апроксимують відсіками розгортних поверхонь і будують розгортки цих відсіків. Сукупність розгорток відсіків розгортних поверхонь, якими замінюється нерозгортна поверхня, називається умовною наближеною розгорткою нерозгортної поверхні.

Побудова розгорток має велике практичне значення, тому що дозволяє виготовляти різноманітні вироби з плоского (листового) матеріалу шляхом його згинання.

16.2. Розгортка многогранних поверхонь

Розгорткою многогранної поверхні є плоска фігура, яка складається з граней цієї поверхні, суміщених з одною площиною.

Для того, щоб при побудові розгортки многогранника його грані зобразились неспотворено, вони суміщаються з площиною, паралельною площині проекцій.

Існує три способи побудови розгортки многогранних поверхонь:

1. спосіб трикутників (триангуляції);

2. спосіб нормального перерізу;

3. спосіб розкочування.

Спосіб трикутників (триангуляції).

Приклад. Побудувати розгортку бічної поверхні піраміди SАВС (рис. 16.1).

Рис. 16.1

Розгортка бічної поверхні піраміди являє собою плоску фігуру, яка складається з трикутників - граней піраміди, і проводиться за наступною схемою:

1) визначається натуральна величина ребер і сторін основи піраміди;

2) в площині креслення послідовно способом засічок будуються натуральні величини трикутників (граней).

На рис. 16.1 довжина ребра піраміди SА визначена способом прямокутного трикутника, ребра SВ - обертанням навколо проектуючої прямої ί  S, ребро SС паралельне фронтальній площині проекцій, а тому проектується на П₂ в натуральну величину. Після того, як визначені довжини ребер S₂А₂,S₂В₂,S₂С₂ переходимо до побудови розгортки. Для цього на вільному полі креслення будуємо трикутник основи А₀В₀С₀, яка на П₁ спроектувалася в натуральну величину. З точки А₀ проводимо дуги радіусом АS , з точки В₀ - дуги радіусом ВS, з точки С₀ - дуги радіусом СS. Точки перетину дуг визначать положення точок S₀ і, відповідно, ребер А₀S₀, В₀S₀, С₀S₀ на розгортці.

Спосіб нормального перерізу.

Приклад. Побудувати розгортку похилої тригранної призми АВСDEF (рис. 16.2).

1). Перерізаємо призму площиною , яка перпендикулярна до бічних ребер. Будуємо переріз заданої призми цією площиною ( 123).

2). Визначаємо довжини сторін  123 (відрізків ламаної лінії, яка отримана при перерізі поверхні призми цією площиною) обертанням навколо фронтально-проектуючої прямої ί  3.

3). Ламану розгортаємо в пряму. Для цього на вільному полі креслення проведемо довільну горизонтальну пряму а. Від довільної точки 1₀, взятої на цій прямій, відкладаємо відрізки 1₀2₀,2₀3₀,3₀1₀, довжини яких дорівнюють довжинам сторін трикутника  123. Через точки 1₀, 2₀, 3₀, 1₀ проведемо прямі, перпендикулярні до прямої а, і відкладемо на них від точок 1₀, 2₀, 3₀, 1₀ відрізки, довжини яких дорівнюють відповідним довжинам бічних ребер (1A,1D,2B,2E, …….). Отримані точки А₀ В₀ С₀ та D₀ E₀ F₀ з'єднуємо прямими. Плоска фігура А₀В₀С₀А₀D₀E₀F₀D₀ являє собою розгортку бічної поверхні призми.

Примітка. На рис.16.2 ребра АD, ВE і СF паралельні площині П₂, тому вони проектуються на цю площину без спотворення. Якщо ребра призми займають довільне положення, то перш ніж перейти до побудови розгортки, слід за допомогою способів перетворення комплексного креслення перевести їх у положення, паралельне до якоїсь площини проекцій.

Щоб отримати повну розгортку призми, необхідно до розгортки бічної поверхні добудувати основи призми - А₀В₀С₀ та D₀E₀F₀, побудова яких очевидна з рис. 16.2.

Примітка. Якщо основи призми займають загальне положення, слід попередньо визначити їх неспотворені розміри.

Рис. 16.2

Спосіб розкочування.

Цей спосіб доцільно використовувати для побудови розгортки поверхні призми у тому випадку, коли основа призми паралельна до якоїсь одної площини проекцій, а її ребра паралельні іншій площині проекцій.

Приклад. Побудувати розгортку похилої тригранної призми АВСDEF (рис. 16.3).

Приймемо за площину розгортки площину , яка проходить через ребро АD і паралельна до фронтальної площини проекцій. Сумістимо грань ADEB з площиною . Для цього уявно розріжемо бічну поверхню призми по ребру АD, а потім повернемо грань ADEB навколо ребра АD (А₂D₂).

Для визначення суміщеного з площиною  положення ребра В₀Е₀ з точки В₂ проводимо промінь, перпендикулярний до А₂D₂, і засікаємо на ньому дугою радіуса А₁В₁, проведеною з центру А₂, точку В₀. Через В₀ проводимо пряму В₀Е₀, паралельну А₂D₂.

Приймаємо суміщене положення ребра В₀Е₀ за нову вісь обертання і повертаємо навколо неї грань ВЕFС до суміщення з площиною . Для цього з точки С₂ проводимо промінь, перпендикулярний до суміщеного ребра В₀Е₀, а за точки В₀ - дугу кола радіусом, рівним В₁С₁; перетин дуги з променем визначить положення точки С₀. Через С₀ проводимо С₀F₀ паралельно В₀Е₀. Аналогічно знаходимо положення ребра А₀D₀. З'єднавши точки А₂В₀С₀А₀ і D₂E₀F₀D₀ прямими, отримаємо фігуру А₂В₀С₀А₀D₀F₀E₀D₂ - розгортку бічної поверхні призми. Для отримання повної розгортки призми досить до якої-небудь з частин ламаної лінії А₂В₀С₀А₀ і D₂E₀F₀D₀ добудувати трикутники основи A₀B₀C₀ та D₀E₀F₀.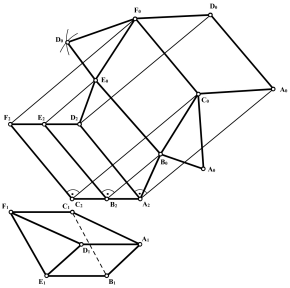

Рис. 16.3