Запитання для самоперевірки

1. У чому полягає загальний метод побудови лінії перетину однієї поверхні іншою?

2. Які точки лінії перетину поверхонь називаються "характерними?"

3. Як будується лінія перетину однієї многогранної поверхні іншою?

4. У яких випадках для побудови лінії перетину однієї поверхні іншою рекомендується використовувати допоміжні січні площини, паралельні площинам проекцій?

5. По яких лініях перетинаються між собою: а) циліндричні поверхні, твірні яких паралельні між собою, б) конічні поверхні зі спільною вершиною?

6. Як можна використати випадок, коли одна з поверхонь, які перетинаються, займає проектуюче положення?

Лекція 14 взаємний перетин поверхонь

14.1. Взаємний перетин поверхонь. Посередник - площина загального положення

В ряді випадків виявляється неможливим підібрати проектуючі площини-посередники, кожна з яких перетинала б одночасно обидві задані поверхні по простих лініях (прямі, кола), але можна підібрати площини - посередники загального положення, які задовольняють даній умові. Особливо ефективним цей підхід виявляється при побудові лінії перетину похилих конічних і циліндричних поверхонь.

Приклад 1. Побудувати лінію перетину двох похилих конусів (рис. 14.1).

(mn)- площина загального положення.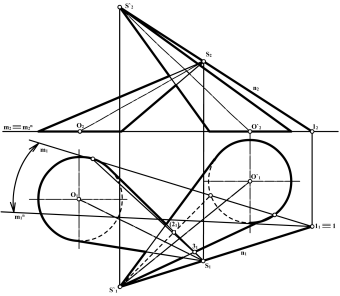

Рис. 14.1

Відомо, що найбільш простим перерізом конуса є трикутник. Цей переріз можна отримати за допомогою площини, що проходить через його вершину. У зв’язку з цим через вершини конусів проводять площину, яка переріже обидва конуси по трикутниках.

Площину  задаємо двома прямими - n, яка проходить через вершини конусів, та m, яка лежить у площині основ конусів.

Побудови виконуємо у такій послідовності:

1). Проводимо проекції прямої n - n₁ і n_2. Будуємо горизонтальний слід прямої n - точку 1.

2). Через точку 1 у П₁ проводимо пряму m (m) так, щоб вона була дотичною до основи першого конуса і перетинала основу другого конуса.

3). Площина (nm) перерізає другий конус по трикутнику і дотикається до першого конуса по твірній. Визначимо дві точки де твірна першого конуса перетне трикутник перерізу другого конуса (2 і 3).

4). Наступне положення прямої m буде таким, щоб горизонтальна проекція її перетинала основи обох конусів. Визначимо положення чотирьох точок.

5). Кінцеве положення площини  буде таким, щоб вона дотикалася до поверхні другого конуса і перетинала поверхню першого конуса. При цьому горизонтальна проекція прямої m - займе положення mⁿ₁.

Приклад 2. Побудувати лінію перетину поверхонь похилого конуса і похилого циліндра (рис. 14.2).

(nm)- загального положення.

Рис. 14.2

1. n - пряма загального положення, проходить через вершину конуса і паралельно твірній циліндра: nS, n//O₁O₁; nS₂, n₂//O₂O₂.

Точка 1 - горизонтальний слід прямої n.

2. Пряма m (m, m) - горизонтальний слід площини  - на П₁ може змінювати положення від mдо m₁ⁿ .

3. Площина  перерізає задані поверхні по твірних. Точки перетину цих ліній між собою визначать шукану лінію перетину двох поверхонь.

Приклад 3. Побудувати лінію перетину двох похилих циліндрів (рис. 14.3).

1. Через довільну точку М(М₁,М₂) проводимо площину (nm). Пряма n паралельна твірним першого циліндра; пряма m - твірним другого.  - площина загального положення. Будуємо горизонтальний слід цієї площини.

2. Паралельно до горизонтального сліду площини  проводимо сліди січних площин у межах від h¹ до hⁿ. Ці площини перерізають циліндричні поверхні по твірних. Точки перетину твірних, які належать одній допоміжній січній площині, визначать точки лінії перетину заданих поверхонь.

Рис. 14.3