Запитання для самоперевірки

1. Як будується крива лінія при перетині кривої поверхні площиною?

2. По яких лініях перетинається циліндрична поверхня площиною, проведеною паралельно до твірної цієї поверхні?

3. Які лінії отримують при перетині циліндра обертання площинами?

4. Як треба провести площину, щоб конічна поверхня перетиналась по прямих лініях?

5. Які криві отримують при перетині конуса обертання площинами?

6. Яку криву отримують при перетині сфери будь-якою площиною і якими можуть бути проекції цієї лінії?

Лекція 12 перетин прямої лінії з поверхнею

12.1. Перетин прямої лінії з поверхнею

Пряма перетинає поверхню другого порядку в двох точках, що називаються точками виходу і входу. Положення цих точок визначаємо за наступною схемою:

1. Через пряму проводимо допоміжну січну площину (найчастіше проектуючу).

2. Будуємо проекції перерізу поверхні січною площиною.

3. Оскільки переріз і пряма лежать в одній площині, то вони між собою перетинаються в двох точках, які є точками перетину прямої з поверхнею.

Щоб отримати раціональне розв'язання цієї задачі, слід вибирати найбільш простий спосіб визначення лінії перерізу поверхні січною площиною. Цього можна досягти двома шляхами:

1. відповідним вибором положення січної площини;

2. переведенням прямої в особливе положення.

Розглянемо кожний з цих варіантів розв'язання.

Варіант 1.

а) допоміжна січна площина - проектуюча

Приклад. Побудувати проекції точок перетину поверхні сфери з прямою загального положення  (рис. 12.1).

1). Через пряму  проводимо допоміжну фронтально-проектуючу площину Σ.

2). Будуємо горизонтальну проекцію перерізу сфери площиною Σ так, як було розглянуто вище (рис. 11.1).

3). Визначаємо А₁ і В₁ - горизонтальні проекції точок зустрічі прямої зі сферою. Їх фронтальні проекції знаходимо за допомогою ліній зв'язку на фронтальній проекції  - ₂. Точка А знаходиться на верхній передній частині сфери, а тому є видимою на П₁ і П₂. Точка В знаходиться на нижній задній частині сфери і тому невидима на П₁ і П₂.

б) допоміжна січна площина - загального положення

Як відзначалося вище, допоміжну площину, що проходить через пряму при перетині нею якоїсь поверхні, слід вибирати так, щоб отримати найпростіші перерізи. Використання допоміжної проектуючої площини не завжди спрощує розв'язання, можливі випадки, коли доцільно вибирати площину загального положення.

Наприклад, при перетині конічної поверхні з прямою лінією такою є площина, яка проходить через вершину і тому перетинає цю поверхню по прямих лініях – твірних конічної поверхні.

При перетині циліндричної поверхні з прямою лінією доцільно проводити допоміжну площину через задану пряму паралельно твірним цієї поверхні – така площина переріже циліндричну поверхню по прямих лініях – твірних циліндричної поверхні.

Приклад. Побудувати проекції точок перетину прямої загального положення  з конусом (рис. 12.2).

Точки перетину А і В будуємо за допомогою площини Σ, яка визначається вершиною конуса і заданою прямою.

Для визначення твірних, по яких площина Σ перетинає конус, треба знайти ще по одній точці для кожної твірної, окрім точки S. Ці точки можуть бути знайдені в перетині горизонтального сліду площини Σ - h^₀ - з колом основи конуса на П₁. h^₀ знаходимо так:

1) будуємо горизонтальний слід прямої  - точку 1;

2) у площині Σ проводимо довільну пряму SK (точка К взята довільно на прямій ) і будуємо її горизонтальний слід - точку 2;

3) 1 2 = h^₀.

Шукані твірні пройдуть через точки 3 і 4.

Точки А і В є точками входу і виходу при перетині прямої  з поверхнею конуса.

Рис. 12.1 Рис. 12.2

Варіант 2. Переведення прямої в особливе положення

При перерізі поверхні сфери площиною в перерізі утворюється коло, яке проектується на площину проекцій у загальному випадку у вигляді еліпсів або прямої та еліпса - якщо січна площина проектуюча (рис. 12.1).

В особливому випадку, коли січна площина паралельна площині проекцій, коло проектується на цю площину проекцій без спотворення. Тому, щоб спростити розв'язання задачі, показаної на рис. 12.1, слід довільно розміщену пряму перевести у положення, паралельне будь-якій площині проекцій. Тоді з'являється можливість провести через пряму допоміжну січну площину, паралельну площині проекцій.

Приклад 1. Визначити точки зустрічі прямої, заданої відрізком АВ з поверхнею сфери (рис. 12.3).

Переводимо пряму, довільно розміщену у просторі, в положення, паралельне площині проекцій. Для цього переходимо від системи Х₁₂ до системи Х₁₄, в якій П₄ // АВ. У цьому випадку горизонтально-проектуюча площина Σ  АВ переріже поверхню сфери по колу радіуса R´, проекція якого на П₁ збігається з А₁В₁, а на П₄ є колом того ж самого радіуса R´. Точки М₄ і N₄ перетину цього кола з А₄В₄ - це проекції на П₄ шуканих точок зустрічі прямої з поверхнею сфери, по яких за допомогою ліній зв’язку визначаємо спочатку М₁ і N₁, а потім М₂ і N₂.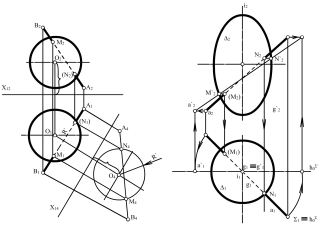

Рис. 12.3 Рис. 12.4

Якщо пряма а (рис. 12.4), що перетинає поверхню обертання, проходить через вісь і цієї поверхні, то переведення прямої а в особливе положення доцільно здійснити шляхом обертання прямої навколо осі і.

Приклад 2. Визначити точки зустрічі прямої а з поверхнею обертання Δ (рис. 12.4).

Горизонтально-проектуюча площина , яку проводимо через пряму а, переріже поверхню обертання по меридіану g. Щоб не будувати спотворену фронтальну проекцію меридіонального перерізу, повертаємо площину  і пряму а, яка в ній знаходиться, навколо осі і до положення, паралельного П₂, тоді g₁ збігається з g'₁ - горизонтальною проекцією головного меридіана, а h^0 з h^0'. Після повороту, пряма а займе положення а'(а'₁, а'₂). За допомогою точок М'₂ та N'₂, в яких а'₂ ∩ g'₂, визначаємо положення М₂ і N₂ та М₁ і N₁.