3). Лінійчаті поверхні з площиною паралелізму.
До цього типу лінійчатих поверхонь відносяться поверхні, всі твірні яких паралельні постійній площині , яку називають площиною паралелізму.
Циліндроїд- лінійчата поверхня , яка має площину паралелізму і дві криволінійні напрямні (рис. 10.9).
Коноїд- лінійчата поверхня, яка має площину
паралелізму, одну криволінійну, а другу
прямолінійну напрямні (рис. 10.10).
Рис. 10.9 Рис. 10.10 Рис. 10.11
Гіперболічний параболоїд (коса площина)- поверхня з двома мимобіжними прямолінійними напрямними, при цьому твірна залишається паралельною площині паралелізму (рис. 10.11).
10.4. Поверхні обертання
В техніці, зокрема в машинобудуванні, поверхні обертання знаходять широке використання. Це пояснюється розповсюдженістю обертального руху і простотою обробки поверхонь обертання на верстатах.
Поверхнею обертання називається поверхня, яка утворюється при обертанні будь-якої твірної (прямої, плоскої або просторової кривої) навколо нерухомої осі (рис. 10.12а).
До визначника поверхні обертання входять твірна m та вісь обертання ί: Q(m, ί).
Точки твірної кривої m описують навколо осі ί кола: кола, утворені в результаті перетину поверхні обертання площинами, перпендикулярними до осі поверхні обертання, називаються паралелями.
Паралель, менша за дві сусідні з обох боків, називається горлом.
Паралель, більша за дві сусідні з обох боків, називається екватором.
Лінії, що
утворюються в результаті перетину
поверхні обертання площинами, які
проходять через вісь, називаються
меридіанами.
Фронтальний меридіан називається
головним.
а) б)
Рис. 10.12
При задаванні поверхні обертання на кресленні (рис. 10.12б) звичайно вказують проекції її осі, головного меридіана та екватора (інколи показують коло, по якому поверхня обертання перетинається з площиною проекцій). При цьому вказують тільки горизонтальну проекцію екватора (або паралелі) і фронтальну проекцію головного меридіана.
Властивості поверхонь обертання.
1). Поверхні обертання мають властивість зміщування. Обертаючись навколо своєї осі, вони можуть зміщуватись без деформації вздовж самої себе.
2). Якщо меридіан поверхні обертання проходить через дві точки поверхні, то він є найкоротшою лінією між цими точками. Всі меридіани рівні між собою.
3). Кожна з паралелей поверхні обертання перетинає всі меридіани під прямим кутом.
4). Кожна з нормалей до поверхні обертання перетинає вісь поверхні.
Поверхні обертання другого порядку. Точка на поверхні.
При обертанні кривої другого порядку навколо її осі утворюється поверхня обертання другого порядку.
Сфера - якщо твірна лінія є коло, а вісь обертання збігається з її діаметром (рис. 10.13).
Еліпсоїд обертання утворюється обертанням еліпса навколо його осі (рис. 10.14).
Параболоїд обертання утворюється обертанням параболи навколо її осі (рис. 10.15).
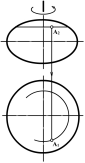
Рис. 10.13 Рис. 10.14 Рис. 10.15
Однопорожнинний гіперболоїд обертання утворюється обертанням гіперболи навколо її уявної осі (рис 10.16).
5. Двопорожнинний гіперболоїд обертання утворюється обертанням гіперболи навколо її дійсної осі (рис. 10.17).
Рис. 10.16 Рис. 10.17
Тор - поверхня 4-го порядку - утворена обертанням кола навколо осі, яка не проходить через центр кола (рис. 10.18).
В залежності від співвідношення величин R - радіуса твірного кола і відстані t від центра кола до осі обертання поверхні тора поділяють на:
відкритий тор (або кільце) при R t - коло не перетинає вісь обертання (рис. 10.18,а);
закритий тор при R t - коло перетинає вісь обертання або дотикається до неї (рис. 10.18,б).
а) б)
Рис. 10.18