9.4. Проекції кола, яке лежить у площині

Коло є найбільш поширеною в техніці плоскою кривою. У загальному випадку коло проектується в еліпс, велика і мала осі якого є проекціями взаємно перпендикулярних діаметрів кола.

Розглянемо положення кола в наступних площинах:

а) рівня

Коло, яке лежить у площині рівня (рис. 9.9) проектується в натуральну величину на ту площину проекцій, до якої паралельна площина, в якій лежить коло. На інші площини проекцій коло проектується в лінії, паралельні осям проекцій.

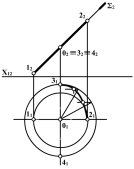
Рис. 9.9 Рис. 9.10

Б) в проектуючій площині

На площину П₂, до якої перпендикулярна площина, в якій лежить коло (рис. 9.10), коло проектується у вигляді відрізка прямої лінії, який дорівнює діаметру кола.

На інші площини коло проектуються у вигляді еліпсів, велика і мала осі яких визначаються з проекцій. Знаючи розміри великої і малої осі еліпса, можна побудувати сам еліпс одним із відомих з креслення способів.

В) в площині загального положення

Дано: площина (hf) -загального положення, центр кола- точка О і радіус кола R (рис. 9.11).

Через центр кола проводимо горизонталь (h) і фронталь (f) площини - таким чином виділяємо фронтальний і горизонтальний діаметри кола. Фронтальний діаметр кола зображається в натуральну величину на фронтальній площині проекцій, а горизонтальний - на горизонтальній.

На площини проекцій П₁ і П₂ коло буде проектуватись в еліпси, у яких велика вісь відома (вона збігається з h₁ i f₂ площини). Малі осі еліпсів будуть перпендикулярні до великих, але нам невідома їх величина.

Величину малої осі еліпса визначаємо таким чином: на П₁ - через точку 2₁ проводимо перпендикуляр до 54, цей перпендикуляр перетинається з колом в точці 2_0. З’єднуємо точку 2₀ з точкою О₁ - через точку А₀ проводимо лінію, яка паралельна 2₀О₁, а через отриману точку В₁ лінію, яка паралельна О₁ 2₁. Точка А₁ визначить розмір малої півосі еліпса. А₁О₁ = О₁С₁.

Нам відомі розміри і положення малої і великої осей еліпса і ми можемо відомим нам способом побудувати еліпс.

Фронтальна проекція кола будується так само, тобто у відповідності з уже побудованою горизонтальною проекцією.

Рис. 9.11

9.5. Просторові криві лінії

Просторові лінії займають більш складне положення у просторі, ніж плоскі криві.

Дана просторова лінія  і точка М на ній (рис. 9.12). Проведемо через цю точку дві січні a і b, які перетинають криву  в точках А і B.

При наближенні точок А і В до точки М січні будуть провертатись навколо точки М і, коли всі три точки співпадуть, займуть положення напівдотичних t i t. Якщо точка М звичайна, то напівдотичні будуть мати протилежне направлення, утворюючи загальну дотичну.

Через дотичну до кривої в точці М можна провести нескінчену кількість площин. Одна з них, яка визначає граничне положення площини, що проходить через три нескінченно близькі точки просторової кривої, називається стичною площиною.

Рис. 9.12 Рис. 9.13

Через точку М кривої  можна провести нескінчену кількість прямих, що будуть перпендикулярні до дотичної. Всі вони лежать у площині, яка називається нормальною площиною. Одна з цих нормалей лежить у стичній площині і називається головною нормаллю n^г.

Друга нормаль, яка перпендикулярна до стичної площини називається бінормаллю n^р (рис. 9.13).

Проекційні властивості просторових кривих ліній такі ж самі як і плоских кривих. Але є і деякі відмінності. Так, наприклад, просторова крива лінія проектується тільки в плоску криву. Зображення точок на проекціях кривих ліній може не відповідати положенню самих точок.

З усіх просторових кривих ліній, що використовуються в техніці, найбільш розповсюджені гвинтові лінії.