7.2. Обертання навколо лінії рівня (спосіб суміщення)

Обертання навколо горизонталі або фронталі застосовують, коли задану плоску фігуру потрібно сумістити з площиною рівня, паралельною площині проекцій. В такому положенні плоска фігура проектується на відповідну площину проекцій в натуральну величину.

Розглянемо спочатку обертання точки А навколо горизонталі (рис. 7.4). Суть перетворення залишається такою ж, як і у випадку обертання навколо осей, які перпендикулярні до площин проекцій.

При обертанні навколо h точка А описує дугу кола у площині обертання . Площина обертання  перпендикулярна до осі обертання:   h. Таким чином,  є горизонтально-проектуючою площиною:   П₁. Центр обертання - точка О. О =   h. Радіус обертання точки А (АО - відрізок прямої загального положення) знаходиться у площині . Якщо радіус обертання точки А стане // П₁, то він суміститься з площиною рівня, паралельною до П₁, в якій знаходиться вісь обертання h. В цій самій площині рівня опиниться і точка А  R. Таким чином, способом прямокутного трикутника визначаємо натуральну величину радіуса обертання точки А навколо h. Натуральну величину радіуса обертання відкладаємо від точки О₁ на ₁ (або за допомогою циркуля горизонтальну проекцію точки переміщуємо в нове положення А₁), оскільки завжди R  . В новому положенні точка А знаходиться з горизонталлю h в одній площині, яка паралельна П₁. Друга проекція А₂ в цьому випадку буде збігатися з проекцією h - h₂.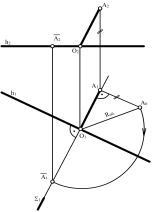

Рис. 7.4

Приклад: Визначити натуральну величину АВС площини загального положення (рис. 7.5).

Для визначення натуральної величини АВС, через точки С і l проводимо горизонталь площини. Ці точки при обертанні будуть нерухомими, оскільки вони знаходяться на осі обертання h. Обертатись будуть лише точки А і В. Вони переміщуються по колах у площинах обертання, перпендикулярних до осі обертання h.

Для визначення положення точки В₁ після обертання, знаходимо натуральну величину радіуса обертання точки В навколо горизонталі h і цим радіусом переводимо горизонтальну проекцію точки В в нове положення.

Радіус обертання точки А можна не знаходити, тому що точка А лежить на прямій l-АВ, а положення двох точок цієї прямої ми визначили.

В  ;   h; А  ;   h.

Рис. 7.5

Проекція Ā₁В₁С₁ є натуральною величину АВС, оскільки площина АВС стала // П₁. Фронтальна проекція АВС збігається з фронтальною проекцією h₂ горизонталі, тобто являє собою пряму лінію.

Запитання для самоперевірки

1. Які основні елементи способу обертання?

2. У чому суть способу обертання навколо осей, перпендикулярних до площин проекцій?

3. Визначте способом обертання навколо проектуючих осей натуральні величини відрізка прямої і трикутника.

4. Як розміститься площина обертання точки, якщо її вісь обертання лише паралельна до пл. П₁ або до пл. П₂ але не перпендикулярна ні до П₁ ні до П₂? Чому при цьому доводиться визначати натуральну величину радіуса обертання?

5. Знайдіть способом суміщення натуральну величину трикутника, що лежить у горизонтально-проектуючій площині.

6. Що є ознакою досягнення горизонтального положення площини, заданої горизонталлю і точкою, при повороті навколо цієї горизонталі і де розміститься фронтальна проекція точки після повороту?