3. Графічне розв’язання рівнянь з параметрами

Алгоритм графічного методу:

1. Знайти область допустимих значень невідомого та параметрів, що входять до рівняння.

2. Виразити параметр як функцію від невідомого: .

3. В системі координат побудувати графік функціїдля тих значеньх, які входять в область визначення рівняння.

4. Знайти точки перетину прямої з графіком.

Можливі випадки:

1. пряма не перетинає графік функції. При цьому значеннярівняння розв’язків не має.

2. пряма перетинає графік функції. Визначити абсциси точок перетину (для цього достатньо розв’язати рівняннявідносно).

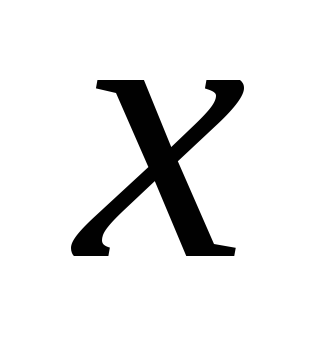5. Записати відповідь

І. Якщо рівняння набуває вигляду

ІІ. Якщо матимемо

У системі координат будуємо графіки функційдлятадля

Далі, знаходимо точки перетину прямої з графіком функціїПрямамає з графіком функціїлише одну спільну точки, абсциса якої дорівнює

Якщо рівняння розв’язків не має, оскільки прямане перетинає графікЯкщо, прямаперетинає графік функціїу двох точках, абсциси якихможна знайти з рівняння

Якщо , то перетином прямоїз графіком функціїє дві точки з абсцисамиде— менший корінь рівняння;— більший корінь рівняння, тобто

(В. Якщо рівняння розв’язку не має;

; )

Приклад. При якому значенні рівняннямає три розв’язки?

 Запишемо рівняння у вигляді

ОДЗ: ,

Побудуємо схематично графіки функцій та

Якщо , то прямаперетинає кривуу трьох точках з абсцисами. (В.)

Вправи для самостійного розв’язання

1. При якому значенні параметра рівняннямає три розв’язки? (В. –26)

2. При якому найбільшому цілому значенні параметра рівняннямає два розв’язки? (В. –16)

3. Розв’язати графічно рівняння .

(В. Якщо

рівняння немає розв’язків.

4. Розв’язати графічно рівняння .

(В. Якщо рівняння розв’язків немає.

Якщо

5.

Дослідження та розв’язання систем лінійних рівнянь з двома невідоми та з параметрами

Дослідити систему рівнянь означає встановити:

• чи є система визначеною тобто має єдиний розв’язок, і при яких умовах;

• чи є система несумісною тобто немає розв’язків, і при яких умовах;

• чи має вона безліч розв’язків і при яких умовах.

Приклад. Дослідити систему рівнянь

де — невідомі;— параметр.

 1. Якщо то система має єдиний розв’язок.

При цьому графіки рівнянь, що входять у систему, мають одну спільну точку, координати якої є розв’язком системи.

2. Якщо то система не має розв’язків.

Графіки рівнянь при цьому є взаємно паралельними прямими.

Якщо то система рівнянь має безліч розв’язків.

Графіки рівнянь збігаються.

Приклад 2. При якому значенні параметра а система має безліч розв’язків?

 Система має безліч розв’язків, якщо

Розв’язати рівняння .

Звідси . З умовимаємо.

(В. )

Приклад 3. При яких значеннях а система не має розв’язків?

 Система не має розв’язків, якщо

Розв’яжемо рівняння

Звідси

Перевіримо умову

Підставимо в останній вираз замість а значення дістанемо

Якщо то системанемає розв’язків.

(В. .)

Приклад. При яких значеннях система рівняньмає розв’язки?

 Система має розв’язки, якщо

тобто

Розв’язуючи систему рівнянь, матимемо

За умовою задачі тобто

Оскільки , то остання система рівносильна системі:

звідси

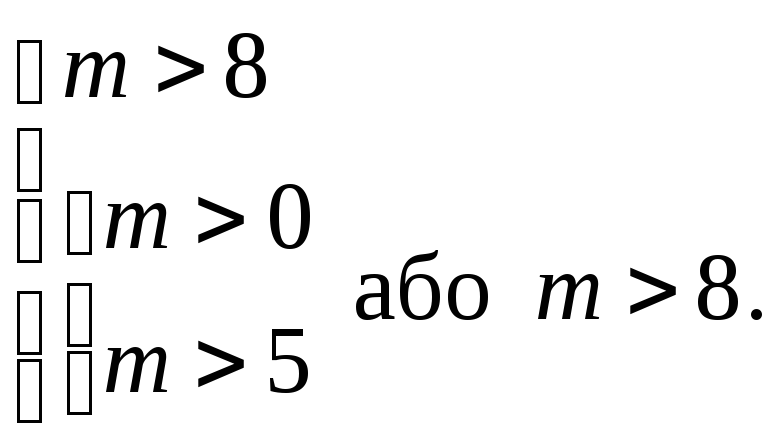
(В. )