Задачі для підготовки до зовнішнього незалежного оцінювання з математики
Дано точки А, В і С, які не лежать в основній площині. Треба побудувати лінію перетину (слід) площини АВС з основною площиною.
Розв’язання: Знаходимо точку Х, в якій пряма ВА перетинає основну площину, і точку Y, в якій пряма ВС перетинає основну площину. Тоді пряма XY являється, очевидно, шуканою (рис.1).

Рис.1.
Дано дві проектуючи площини. Треба побудувати їх лінію перетину.
Розв’язання:
Нехай
одна проектуюча площина визначена на
рисунку проектуючими
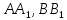 ,
а
друга ― проектуючи ми
,
а
друга ― проектуючи ми
 .
Припустимо, що сліди
.
Припустимо, що сліди
 даних площин перетинаються в точці
даних площин перетинаються в точці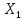 .
Проведемо через цю точку проектуючи
пряму
.
Проведемо через цю точку проектуючи
пряму .
Доведемо, що ця пряма являється шуканою
лінією перетину даних площин. Спарвді,
ця лінія паралельна прямій
.
Доведемо, що ця пряма являється шуканою
лінією перетину даних площин. Спарвді,
ця лінія паралельна прямій ( оскільки всі проектуючі паралельні),
отже, вона лежить в площині
( оскільки всі проектуючі паралельні),
отже, вона лежить в площині .
За аналогічною причиною вона повинна
лежати і вплощині
.
За аналогічною причиною вона повинна
лежати і вплощині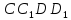 .
Тому пряма
.
Тому пряма
 є шуканою лінією перетину даних площин
(рис.2).
є шуканою лінією перетину даних площин
(рис.2).

Рис. 2.
Дано: проектуючи площина
 і пряма CD
(
і пряма CD
( ).Побудувати
точку зустрічі даної прямої з даною
площиною.
).Побудувати
точку зустрічі даної прямої з даною
площиною.
Розв’язання:
Пряма
CD
визначає проектуючу площину
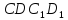 ,
яка проходить через неї. Будуємо лінію
перетину
,
яка проходить через неї. Будуємо лінію
перетину
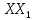 обох проектуючи площин ( для чого
достатньо знайти точку
обох проектуючи площин ( для чого
достатньо знайти точку перетину слідів
перетину слідів і провести через неї проектуючи пряму).
Точка Х, в якій ця пряма перетинає дану
пряму, і є шуканою. Наспаравді, вона
лежить на прямійCD
і на площині
і провести через неї проектуючи пряму).
Точка Х, в якій ця пряма перетинає дану
пряму, і є шуканою. Наспаравді, вона
лежить на прямійCD
і на площині
 ,
отже, вона являється точкою їх
перетину(рис.3).
,
отже, вона являється точкою їх
перетину(рис.3).
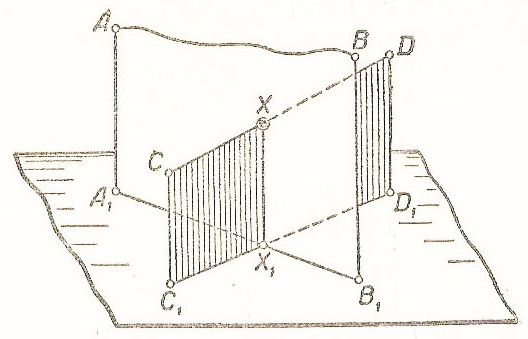
Рис.3.
Дано проектуючу площину
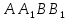 і точку C
(
і точку C
( ).
Провести через цю точку площину рівня
і побудувати лінію перетину її з даною
проектуючою площиною.
).
Провести через цю точку площину рівня
і побудувати лінію перетину її з даною
проектуючою площиною.
Розв’язання:
З’єднуємо
 з
з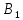 і проводимо
і проводимо
 .ТодіCD
― лінія рівня, яка лежить в шуканій
площині рівня. Тому точка D
є точкою лінії перетину площини рівня
з площиною
.ТодіCD
― лінія рівня, яка лежить в шуканій
площині рівня. Тому точка D
є точкою лінії перетину площини рівня
з площиною
 .
Оскільки ця лінія перетину являється
одночасно і лінією рівня, то вона повинна
бути паралельною сліду
.
Оскільки ця лінія перетину являється
одночасно і лінією рівня, то вона повинна
бути паралельною сліду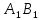 .
Отже, маємо
.
Отже, маємо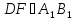 (рис.4).
(рис.4).

Рис.4.
Дано дві площини
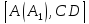 і
і
 .
Побудувати лінію їх перетину.
.
Побудувати лінію їх перетину.
Розв’язання:
Будуємо
проектуючу площину
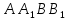 і обидві лінії її перетину з двома даними
площинами: AX
і
BY.
Знаходимо точку перетину останніх ―
K.
Зєднуємо K
з
точкою L
перетину
слідів даних площин, отримаємо шукану
лінію перетину KL(рис.5).
і обидві лінії її перетину з двома даними
площинами: AX
і
BY.
Знаходимо точку перетину останніх ―
K.
Зєднуємо K
з
точкою L
перетину
слідів даних площин, отримаємо шукану
лінію перетину KL(рис.5).

Дано зображення куба
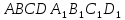 .
Побудувати точку, в якій перетинається
пряма
.
Побудувати точку, в якій перетинається
пряма (М – середина ребра
(М – середина ребра )
з площиною ABCD.
)
з площиною ABCD.
Розв’язання:
Шукана
точка О
лежить на прямій, по якій перетинаються
площина ABCD
і площина, якій належить пряма
 .
Таких площин нескінченна множина. Але
ми з них обираємо таку, пряму перетин
якої з площиною АВС
легко побудувати. Оскільки ребра
.
Таких площин нескінченна множина. Але
ми з них обираємо таку, пряму перетин
якої з площиною АВС
легко побудувати. Оскільки ребра
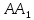 і
і паралельні, то вони лежать в одній
площині, яка перетинається з площиноюАВС
по прямій АС.
Шукана точка О
лежить на прямих АС
і
паралельні, то вони лежать в одній
площині, яка перетинається з площиноюАВС
по прямій АС.
Шукана точка О
лежить на прямих АС
і
 ,
розташованих в площині
,
розташованих в площині .
Тому, побудувавши пряміАС
і
.
Тому, побудувавши пряміАС
і
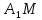 ,
знайдемо шукану точкуО(рис.6).
,
знайдемо шукану точкуО(рис.6).
Рис.6.
Дано зображення куба
 .
Побудувати точкуО
перетину прямої
.
Побудувати точкуО
перетину прямої
 (М – довільна точка ребра
(М – довільна точка ребра )
з діагональною площиною
)
з діагональною площиною
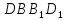 куба.
куба.
Розв’язання:
Шукана
точка належить одночасно площинам
 і
і
 (оскільки
цій площині належить пряма
(оскільки
цій площині належить пряма
 ).
Отже, точка О належить прямій, по якій
перетинаються площини
).
Отже, точка О належить прямій, по якій
перетинаються площини і
і .
Перетин цієї прямої з прямою
.
Перетин цієї прямої з прямою є шуканою точкою О.
є шуканою точкою О.
Побудова:Будуємо
діагоналі граней куба АС,
 ,
,
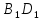 ,
BD.
Отримуємо
точки К
і Р.
Пряма КР
― це пряма, по якій перетинаються площини
,
BD.
Отримуємо
точки К
і Р.
Пряма КР
― це пряма, по якій перетинаються площини
 і
і .
Будуємо
відрізки РК
і
.
Будуємо
відрізки РК
і
 .
Отримуємо в їх перетині шукану точкуО(рис.7).
.
Отримуємо в їх перетині шукану точкуО(рис.7).
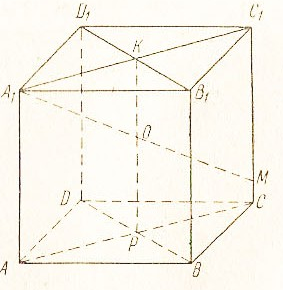
Рис.7.
Дано зображення куба
 .
Побудувати
пряму,
в якій перетинаються площини
.
Побудувати
пряму,
в якій перетинаються площини
 і
ВСМ
(М – довільна
точка грані
і
ВСМ
(М – довільна
точка грані
 ).
).
Розв’язання:
Оскільки
 ,
то шукана пряма також паралельна AD
і
BC.
Крім того, пряма ВС паралельна площині
,
то шукана пряма також паралельна AD
і
BC.
Крім того, пряма ВС паралельна площині
 . Тому
пряма, по якій перетинаються площини
МВС
і
. Тому
пряма, по якій перетинаються площини
МВС
і
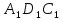 ,
також паралельна ВС, а значить, іAD.
І,
нарешті, прямі перетину площин МВС з
площинами
,
також паралельна ВС, а значить, іAD.
І,
нарешті, прямі перетину площин МВС з
площинами
 і
і паралельні між собою. На основі викладеного
виконуємо наступні побудови: В площині
паралельні між собою. На основі викладеного
виконуємо наступні побудови: В площині
 через точку М проводимо відрізок
через точку М проводимо відрізок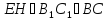 .
Отримуємо точки
.
Отримуємо точки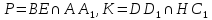 .
Пряма
РК ― шукана (рис.8).
.
Пряма
РК ― шукана (рис.8).

Рис.8.
Дано зображення чотирикутної призми
 і відрізкаРК,
який лежить в площині грані
і відрізкаРК,
який лежить в площині грані
 .
Побудувати точки перетину прямої РК з
площинамиABCD
і
.
Побудувати точки перетину прямої РК з
площинамиABCD
і
 .
.
Розв’язання:
Пряма РК
лежить в площині
 ,
яка перетинається площиною АВС
по прямій ВС,
тому точка Х
перетину прямої РК
з площиною
АВС
лежить на продовженні ребра ВС.
Точка Y
перетину прямої РК
з площиною
,
яка перетинається площиною АВС
по прямій ВС,
тому точка Х
перетину прямої РК
з площиною
АВС
лежить на продовженні ребра ВС.
Точка Y
перетину прямої РК
з площиною
 лежить на прямій перетину площин
лежить на прямій перетину площин і
і
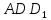 .
Будуємо точки
.
Будуємо точки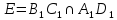 і
і
 .Отримуємо
пряму EF,
по
якій перетинаються площини
.Отримуємо
пряму EF,
по
якій перетинаються площини
 і
і
 .
.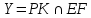 (рис.9).
(рис.9).

Рис. 9.
Дано зображення похилої призми
 і точкиM,
K,
P,
F,
E,
H
― по одній на кожній грані:
і точкиM,
K,
P,
F,
E,
H
― по одній на кожній грані:
 .
Побудувати лінію перетину площинMKE
і PFH(рис.10).
.
Побудувати лінію перетину площинMKE
і PFH(рис.10).

Рис.10.
Розв’язання: Ця задача може бути вирішена різними шляхами. Наведемо одне з найбільш простих. Будуємо дві трикутні призми:
а)
 ― її
бокові ребра паралельні боковим ребрам
даної призми і проходять через точки
P,
H,
F;
її площини основ співпадають з площинами
даної призми;
― її
бокові ребра паралельні боковим ребрам
даної призми і проходять через точки
P,
H,
F;
її площини основ співпадають з площинами
даної призми;
б)
 ―
її бокові ребра паралельні боковим
ребрам даної призми і проходять через
точки M,
K,
E.
ЇЇ площини основ співпадають з площинами
даної призми.
―
її бокові ребра паралельні боковим
ребрам даної призми і проходять через
точки M,
K,
E.
ЇЇ площини основ співпадають з площинами
даної призми.
Після цього будуючи прямі, по яким дані в умові задачі площини перетинаються з основами даної призми.
 ;
XY
― пряма
перетину площини HFP
з
площиною ABC.
;
XY
― пряма
перетину площини HFP
з
площиною ABC.Проводимо в площині
 через точкуР
пряму а,
паралельну XY.
По прямій а
площина HFP
перетинається з площиною
через точкуР
пряму а,
паралельну XY.
По прямій а
площина HFP
перетинається з площиною
 .
. ,
ZG
― пряма
перетину площини
MKE
з площиною
,
ZG
― пряма
перетину площини
MKE
з площиною
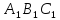 .
.Проводимо в площині АВС через точку М пряму b, паралельну прямій ZG. По прямій b площина MKE перетинається з площиною ABC.
Q ― точка перетину прямих XY і b.
N ― точка перетину прямих GZ і a.
Пряма QN ― шукана.
Таким чином, для цього рішення характерні такі етапи:
а) побудова прямих, по яких перетинається дана площина з паралельними площинами (основами призми);
б) безпосередня побудова перетину даних площин.
(Використовувати метод слідів)
На ребрах куба
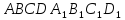 дано
точки P,
Q,
R
такі, що
дано
точки P,
Q,
R
такі, що
 .
Побудувати переріз куба площиноюPQR
.
.
Побудувати переріз куба площиноюPQR
.
Розв’язання:
З’ясуємо спочатку розв’язується ця
задача чи ні. Нехай фігура
 є зображенням куба. Це зображення повне.
Також зрозуміло, що, маючи на зображенні
точки P,
Q
і R
― проекції точок
є зображенням куба. Це зображення повне.
Також зрозуміло, що, маючи на зображенні
точки P,
Q
і R
― проекції точок
 ,
ми можемо знайті і другорядні проекції
точок
,
ми можемо знайті і другорядні проекції
точок .
Для цього достатньо виконати в площині
зображення внутрішнього паралельного
проектування, наприклад, в напрямку,
паралельному (
.
Для цього достатньо виконати в площині
зображення внутрішнього паралельного
проектування, наприклад, в напрямку,
паралельному (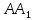 ).
Таким чином, ми знайдемо точки
).
Таким чином, ми знайдемо точки і
прийдемо до висновку, що зображення
перетинаючої площини є заданим. Тоді
задача про знаходження перетину площини,
заданої точками P,
Q
і R,
з поверхнею куба розв’язується. Перейдемо
безпосередньо до побудови перерізу.
Перш за все знайдемо слід перетинаючої
площини ― лінію перетину площини PQR
і
площини
ABC.
і
прийдемо до висновку, що зображення
перетинаючої площини є заданим. Тоді
задача про знаходження перетину площини,
заданої точками P,
Q
і R,
з поверхнею куба розв’язується. Перейдемо
безпосередньо до побудови перерізу.
Перш за все знайдемо слід перетинаючої
площини ― лінію перетину площини PQR
і
площини
ABC.
Оскільки
 ,
а
,
а ,
то
,
то
 .Оскільки
.Оскільки
 ,
а
,
а ,
то
,
то
 .Таким
чином, точка Х є спільною точкою площин
PQR
і
ABC.
Точка R
також
є спільною точкою цих площин. Тоді XR
― пряма, по якій перетинаються площини
PQR
і
ABC.
.Таким
чином, точка Х є спільною точкою площин
PQR
і
ABC.
Точка R
також
є спільною точкою цих площин. Тоді XR
― пряма, по якій перетинаються площини
PQR
і
ABC.
XR ― слід перетинаючої площини.
 .
.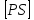 ,
, .
.
Оскільки
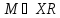 ,
a
,
a
 і
і
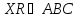 ,
то
,
то
 і
і
 .
Оскільки
.
Оскільки
 ,
a
,
a
 .Точка
Р також є спільною точкою цих площин.
Тому МР ― пряма, по якій перетинаються
площина PQR
з
площиною бокової грані
.Точка
Р також є спільною точкою цих площин.
Тому МР ― пряма, по якій перетинаються
площина PQR
з
площиною бокової грані
 куба.
куба.
 ,
, ,
, .
.
Аналогічно знаходимо далі точку N і виконуємо побудови:
 ,
, ,
, .
.
Оскільки за побудовою вершини багатокутника SPKQLR є точками, які лежать в січній площині PQR і належать ребрам куба, то багатокутник SPKQLR ― шуканий переріз. Оскільки по змісту задачі P, Q і R не лежать на одній прямій, то задача має єдиний розв’язок (рис.11).

Рис.11.
Побудувати переріз трикутної піраміди площиною, заданою її слідом на площині основи піраміди, який не перетинає сторін основи, і точкою на бічній грані піраміди.
Розв’язання:
На рисунку дано зображення піраміди
SABC,
слід MN
площини перерізу на площині основи ABC
і точку D
на грані BSC.
Площина SAD
має спільну точку
 зі слідом MN,
а тому і спільну пряму
зі слідом MN,
а тому і спільну пряму
 з площиною перерізуDMN.
Пряма
з площиною перерізуDMN.
Пряма
 перетне сторонуSA
в якійсь точці K,
яка належатиме площині перерізу. Знайдемо
точку
перетне сторонуSA
в якійсь точці K,
яка належатиме площині перерізу. Знайдемо
точку
 .
Тоді пряма
.
Тоді пряма перетне
бічне реброSC
в точці F,
а пряма FD
перетне ребро SB
в точці L.
KFL
― шуканий переріз (рис.12).
перетне
бічне реброSC
в точці F,
а пряма FD
перетне ребро SB
в точці L.
KFL
― шуканий переріз (рис.12).

Рис.12.
Побудувати переріз п’ятикутної призми площиною, заданою трьома точками, дві з яких лежать на бічних гранях, а третя ― на бічному ребрі.
Розв’язання:
Дано зображення п’ятикутної призми
 і три точки площини перерізу
і три точки площини перерізу
 (рис.).Для знаходження точок перетину
січної площиниMNK
з ребрами призми використаємо метод
слідів і паралельне внутрішнє проектування
в напрямі бічних ребер призми. Проекціями
даних точок M,
N,
K
у площині основи будуть точки
(рис.).Для знаходження точок перетину
січної площиниMNK
з ребрами призми використаємо метод
слідів і паралельне внутрішнє проектування
в напрямі бічних ребер призми. Проекціями
даних точок M,
N,
K
у площині основи будуть точки
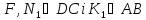 .
Тоді
.
Тоді , прямаXY
― слід площини перерізу в площині основи
призми.
, прямаXY
― слід площини перерізу в площині основи
призми.
Побудуємо
точку
 ,
тоді
,
тоді
 і
і
 .
.
Аналогічно,
побудувавши точку
 ,
одержимо точки
,
одержимо точки
 і
і
 .Пятикутник
MQRLS
―
шуканий переріз (рис.13).
.Пятикутник
MQRLS
―
шуканий переріз (рис.13).
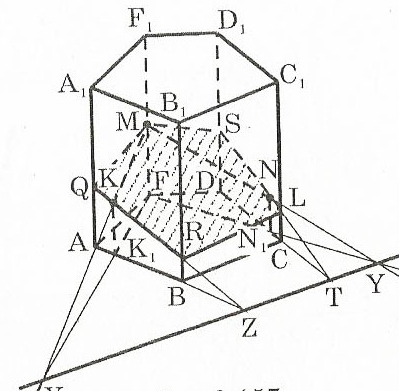
Рис.13.
Побудувати переріз чотирикутної піраміди площиною, заданою трьома точками на різних бічних гранях піраміди.
Розв’язання:
Дано зображення чотирикутної піраміди
SABCD
і точок E,
F,
K
на бічних гранях SBC,
SAD,
SAB
відповідно. Розвязування задачі зводиться
до знаходження точки перетину січної
площини EFK
з одним із ребер піраміди. Використаємо
метод слідів: побудуємо слід XY
січної площині у площині основи піраміди:
 ,
де
,
де
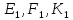 ― центральні проекції точокF,
K,
E
у внутрішньому проектуванні з центра
S
на площину основи піраміди.
― центральні проекції точокF,
K,
E
у внутрішньому проектуванні з центра
S
на площину основи піраміди.
Для
знаходження точки Q
на ребрі SC
проведемо пряму BC
до перетину зі слідом XY
у точці Z,
тоді

 .Далі
проводимо прямуRK
до перетину з ребром SA
в точці M,
пряму MF
до перетину з ребром SD
в точці N
(рис.). Чотирикутник QRMN
― шуканий переріз (рис.14).
.Далі
проводимо прямуRK
до перетину з ребром SA
в точці M,
пряму MF
до перетину з ребром SD
в точці N
(рис.). Чотирикутник QRMN
― шуканий переріз (рис.14).

Рис. 14.
Побудувати переріз п’ятикутної піраміди площиною, заданою трьома точками, дві з яких лежать на бічних ребрах, а одна ― на грані піраміди.
Розв’язання:
Дано зображення пятикутної піраміди
SABCDF
і точок
 (рис.15).
(рис.15).
Побудуємо
слід
XY
площини перерізу LMN
у площині основи піраміди:
 (у площиніSNM
(у площиніSNM
 іD
― центральні проекції точок N
і M
відповідно),
іD
― центральні проекції точок N
і M
відповідно),
 (у площиніSLM,
точки B
і D
― центральні проекції точок L
і M
відповідно, S
― центр проектування). Далі знайдемо
точки перетину січної площини з бічними
ребрами піраміди:
(у площиніSLM,
точки B
і D
― центральні проекції точок L
і M
відповідно, S
― центр проектування). Далі знайдемо
точки перетину січної площини з бічними
ребрами піраміди:
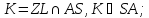 де
де
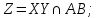

 ,
де
,
де
 .
.
LKQME ― шуканий переріз.

Рис.15.
(Використовувати метод внутрішнього проектування)
Побудувати переріз куба
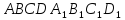 площиною, яка проходить через вершину
площиною, яка проходить через вершину ,
точкуN
на
ребрі АВ
і на M
ребрі
AD.
,
точкуN
на
ребрі АВ
і на M
ребрі
AD.
Розв’язання:
Використаємо внутрішнє проектування
паралельно бічним ребрам куба на площину
нижньої основи: проекцією точки
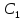 буде точка
C,
точки M
і N
збігаються зі своїми проекціями (рис.).
Знайдемо точку перетину площини
буде точка
C,
точки M
і N
збігаються зі своїми проекціями (рис.).
Знайдемо точку перетину площини
 з проектуючою прямою
з проектуючою прямою
 ,
тоді
,
тоді
 .
Прямі
.
Прямі
 і
і
 перетинають ребра куба
перетинають ребра куба
 і
і
 у точках
у точках
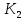 і
і
 відповідно. Многокутник
відповідно. Многокутник
 ―
шуканий переріз (рис.16).
―
шуканий переріз (рис.16).

Рис.16.
Побудувати переріз п’ятикутної призми площиною, що проходить через дані три точки, дві з яких лежать на бічних ребрах, а третя ― на бічній грані призми.
Розв’язання:
Нехай
 ― зображення даної призми, точки
― зображення даної призми, точки
 належать площині перерізу (рис.17).
належать площині перерізу (рис.17).
Побудуємо
переріз призми методом внутрішнього
проектування: точки A,
D,
 ― проекції даних точокM,
N,
K
у площині основи призми. Знайдемо точку
― проекції даних точокM,
N,
K
у площині основи призми. Знайдемо точку
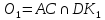 ― це проекція точки
― це проекція точки і
і ,
де
,
де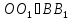 .Тоді
прямаMO
перетне ребро
.Тоді
прямаMO
перетне ребро
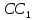 у точціR,
а пряма RK
перетне ребро
у точціR,
а пряма RK
перетне ребро
 у точціQ.
у точціQ.
Далі
побудуємо точку
 та її прообраз
та її прообраз ,
де
,
де ,
тоді прямаRL
перетне ребро
,
тоді прямаRL
перетне ребро
 у точціP.
Переріз MQRNP
― шуканий.
у точціP.
Переріз MQRNP
― шуканий.
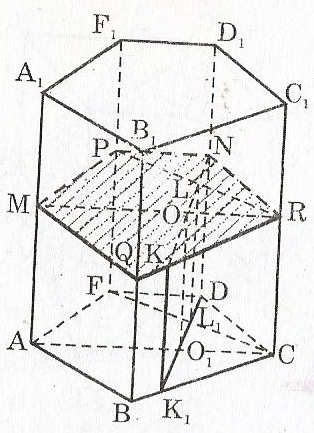
Рис.17.
Дана п’ятикутна піраміда SABCDF . Побудувати переріз площиною, заданою трьома точками M, N, P на бічних ребрах.

Рис.18.
Розв’язання:
Дані точки лежать на ребрах
 піраміди SABCDF
(рис.18).Розвязання задачі передбачає
знаходження точок перетину січної
площини MNP
з бічними ребрами SB
і SC.
Використаємо метод центрального
внутрішнього проектування на площину
основи піраміди з центром S:
точки A,
F,
D
― центральні проекції точок M,
N,
P
відповідно, відрізок AD
― центральна проекція відрізка MP.
Для знаходження точки перетину січної
площини з ребром SB
проведемо відрізок BF
основи, який перетне відрізок AD
у точці
піраміди SABCDF
(рис.18).Розвязання задачі передбачає
знаходження точок перетину січної
площини MNP
з бічними ребрами SB
і SC.
Використаємо метод центрального
внутрішнього проектування на площину
основи піраміди з центром S:
точки A,
F,
D
― центральні проекції точок M,
N,
P
відповідно, відрізок AD
― центральна проекція відрізка MP.
Для знаходження точки перетину січної
площини з ребром SB
проведемо відрізок BF
основи, який перетне відрізок AD
у точці
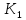 ,
ця точка є центральною проекцією точки
,
ця точка є центральною проекцією точки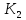 ,
яка лежить на відрізкуMP:
,
яка лежить на відрізкуMP:
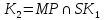 .
Тоді точка
.
Тоді точка ―
шукана вершина перерізу на ребрі
SB.
Аналогічно знаходимо точку
F
на ребра
SC:
проводимо FC,
дістанемо точку
―
шукана вершина перерізу на ребрі
SB.
Аналогічно знаходимо точку
F
на ребра
SC:
проводимо FC,
дістанемо точку
 в перетині з AD,
яка є проекцією точки
в перетині з AD,
яка є проекцією точки
 ,
а потім і точку
,
а потім і точку
 .MNPFK
―
шуканий переріз.
.MNPFK
―
шуканий переріз.
Через середини двох суміжних сторін основи правильної чотирикутної призми, сторона основи якої дорівнює а, проведена площина, що перетинає три бічні ребра і нахилена до площини основи під кутом α. Знайдіть площу одержаного перерізу.
Розв’язання:
Побудова зображення. Нехай
 ― зображення
правильної чотирикутної призми (рис.19).
Візьмемо
точки M
і
N
такі, що
― зображення
правильної чотирикутної призми (рис.19).
Візьмемо
точки M
і
N
такі, що
 .
.

Рис.19.
Переріз
проходить через пряму MN,
що сполучає середини суміжних сторін
основи. Тому MN
― ребро двогранного кута між площиною
основи і площиною перерізу. Прийнявши
за одну сторону лінійного кута діагональ
AC
основи, маємо, що друга його сторона RK
повинна лежати в площині діагонального
перерізу
 .
Дійсно
.
Дійсно ,
тому
,
тому
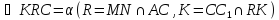 .
На бічній грані
.
На бічній грані лежить точкаK,
яка належить і перерізу. Другою точкою,
що належить і перерізу, і грані
лежить точкаK,
яка належить і перерізу. Другою точкою,
що належить і перерізу, і грані
 ,
буде точка
,
буде точка ,
отже, прямаKP
є лінією перетину площини грані
,
отже, прямаKP
є лінією перетину площини грані
 і площини перерізу, вона перетне ребро
і площини перерізу, вона перетне ребро у точціG.
Точки N
і G
― спільні точки перерізу і грані
у точціG.
Точки N
і G
― спільні точки перерізу і грані
 ,
отже,NG
― лінія перетину грані
,
отже,NG
― лінія перетину грані
 з площиною перерізу. Основу призми
площина перерізу перетинає по прямійMN.
Точка
з площиною перерізу. Основу призми
площина перерізу перетинає по прямійMN.
Точка
 є спільною точкою грані
є спільною точкою грані і площини перерізу, як і точкаK,
тому FK
― лінія їх перетину і
і площини перерізу, як і точкаK,
тому FK
― лінія їх перетину і
 .
Отже, перерізом призми площиною є
п’ятикутникGNMLK.
.
Отже, перерізом призми площиною є
п’ятикутникGNMLK.
2.Обчислення
площі перерізу. П’ятикутник BCDMN
є проекцією перерізу
GNMLK
на площину основи, тому
 . Але
. Але
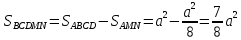 .Тому
.Тому
 .
.
Найменше
значення площі перерізу буде при
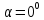 ,
у цьому випадку перерізом буде пятикутникBCDMN
і
,
у цьому випадку перерізом буде пятикутникBCDMN
і
 .
Найбільшою площа перерізу за даної
умови задачі буде тоді, коли точка К
суміститься з вершиною
.
Найбільшою площа перерізу за даної
умови задачі буде тоді, коли точка К
суміститься з вершиною
 ,
у цьому випадку
,
у цьому випадку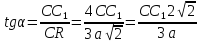 і
і
 ― найбільше
допустиме значення кута α. Отже,
― найбільше
допустиме значення кута α. Отже,
 .
.
Відповідь:
 .
.
Довжина сторони основи правильної чотирикутної піраміди дорівнює а. Площина, яка проходить через сторону основи піраміди і середню лінію протилежної бічної грані, утворює з площиною основи кут
 .
Обчислити об’єм піраміди.
.
Обчислити об’єм піраміди.

Рис.20.
Розв’язання:
1.Побудова
зображення.
Будуємо зображення правильної чотирикутної
піраміди SABCD:
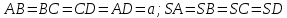 (рис.20).
(рис.20).
ABCD
― квадрат,
проведемо його середні лінії (вісі
симетрії). Вершина S
проектується в точку О їх перетину (і
діагоналей основи). Проведемо середню
лінію MN
грані DSC,
тоді
 і ABNM
― переріз, який має форму рівнобедреної
трапеції. PF
― її вісь симетрії:
і ABNM
― переріз, який має форму рівнобедреної
трапеції. PF
― її вісь симетрії:
 ,
тоді
,
тоді
 ― як лінійний кут двогранного кута з
ребромAB.
― як лінійний кут двогранного кута з
ребромAB.
2.Обчислення
об’єму.
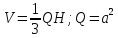 .
Треба
знайти H=SO.
Зробимо це геометричним способом. FK
― вісь симетрії основи, тоді
.
Треба
знайти H=SO.
Зробимо це геометричним способом. FK
― вісь симетрії основи, тоді
 (з
(з
 ).Проведемо
).Проведемо
 З
З
 і
і
 .
.
Відповідь:
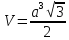 .
.
Комп’ютерна підтримка навчання учнів розв’язуванню стереометричних задач на побудову
Підвищення результативності вивчення математики можливе шляхом систематичного використання різних педагогічних програмних засобів (ППЗ).
В галузі шкільної освіти взято курс на гуманізацію і демократизацію навчання, а головною його метою стає розвиток особистості як найвищої цінності суспільства. Одним із напрямків формування особистості школяра як творчої, розвитку позитивних якостей кожного учня, його потенційних можливостей є використання на уроках ППЗ з математики. Застосування програмних засобів навчання математики з урахуванням інтересів і здібностей учнів сприятиме становленню всебічно розвиненої особистості.
Одним із засобів візуалізації математичної задачі та її розв'язку, який робить діалог учня та вчителя більш доступним та евристичним, є педагогічні програмні засоби: «Візуальна стереометрія»; «Живая математика»; «GeoGebra»; «Cabri 3D»; «Blender»; «Grand 3D»; «Stereo». Дані ППЗ розроблені відповідно до навчальної програми з математики для 11 класу загальноосвітніх навчальних закладів. Завдяки застосуванню цих програм навчання можна здійснювати розвивальними методами. В ППЗ наведена значна кількість стереометричних задач на побудову перерізів многогранників, що унаочнюють графічні зображення та флеш-моделі, що дозволяють переглянути покрокову побудову перерізу. Ми звернимо особливу увагу на такі програми як «Grand 3D»; «Cabri 3D» та «GeoGebra».
Ці завдання можна використовувати при вивченні таких курсів математики, як загальноосвітній, прикладний, загальнокультурний та поглиблений. ППЗ призначений для використання вчителем і учнями безпосередньо в процесі навчання - на уроках, на заняттях гуртка чи факультативу, при самостійній роботі вдома, а також для ефективної підготовки до контрольних робіт та ЗНО. На уроках геометрії його можна використовувати при поясненні нового матеріалу, закріпленні знань і вмінь, організації контролю навчальних досягнень учнів. Це значно підвищуватиме продуктивність праці як вчителя, так і учнів за рахунок наглядності представленого матеріалу.
Підготовлений ППЗ допоможе вчителю математики у формуванні таких позитивних якостей особистості школяра, як розумова активність, пізнавальна самостійність, пізнавальний інтерес, потреба в самоосвіті, здатність адаптуватися до умов, що змінюються, ініціатива, творчість. Новизну даного матеріалу забезпечує унікальна класифікація задач на побудову перерізів многогранників.
 Тому,
розглянемо можливості використання
існуючих програмних педагогічних
засобів, а саме «GRAN-3D»,
«STEREO»
під час вивчення дисциплін
фізико-математичного циклу.
Тому,
розглянемо можливості використання
існуючих програмних педагогічних
засобів, а саме «GRAN-3D»,
«STEREO»
під час вивчення дисциплін
фізико-математичного циклу.
На прикладі ППЗ GRAN-3D розв'язування будь-якої задачі зводиться до створення моделі стереометричного об' єкта і виконання операцій, що фігурують в умові задачі. Даний програмний засіб дозволяє оперувати моделями таких геометричних та просторових об' єктів як точка, відрізок (ламана), площина, многогранник, поверхня обертання.
Точки, відрізки, ламані та площини можна задавати двома способами: або безпосередньо ввести необхідні просторові координати з клавіатури, або вказати їх на екрані.
Для спрощення задання деяких типів стереометричних об' єктів, що вивчаються у школі, програму оснащено послугою «Створити базовий об'єкт», після активізації якої у вікні «Задання базових стереометричних об 'єктів» з'являться доступні засоби для швидкого створення цих об'єктів.
Відразу після створення або модифікації моделей об' єктів за програмою автоматично обчислюються деякі характеристики цих об' єктів. Так, для ламаної обчислюється її довжина, а якщо ламана замкнена, то також обчислюється площа області, обмеженої ламаною.
Над об'єктами можна виконувати операції паралельного перенесення, повороту, зміни розмірів. Разом з тим, можливе виконання перерізів опуклих многогранників площинами, результатом чого є утворення нових многогранників, якими надалі можна оперувати як окремими просторовими об' єктами.
Завдяки перевагам подання графічних та інших даних програмними засобами закладються істотні передумови успішного викладу навчального матеріалу, а саме: ефективний та раціональний розподіл навчального часу протягом уроку; емоційне включення, гностичність та емоційне сприйняття математичних даних учнями. Розглянемо процес розв' язування деякої стереометричної задачі обчислювального характеру з використанням GRAN-3D та методично опишемо хід її розв'язування.
Задача. Правильну п'ятикутну піраміду, висота якої 5 лін. од., а сторона основи 3 лін. од., перетнуто площиною, що проходить через сторону основи і середину протилежного бічного ребра піраміди. Знайти площу та периметр утвореного перерізу піраміди.

В умові фігурують об'єкти «правильна п'ятикутна піраміда», «точка» (як середина бічного ребра піраміди), «площина», «переріз» (як об'єкт - результат виконання операції «переріз»). Отож необхідно створити моделі відповідних об'єктів, що задовольняють умову задачі та виконати операцію «переріз».
Для створення моделі піраміди зручно скористатися послугою програми «Створити базовий об'єкт». У вікні «Задания базових стереометричних об'єктів», що з'явиться, на вкладниці «Правильна піраміда» встановимо лівий перемикач у положення «Висота» і введемо у поле введення під цим перемикачем значення «5». Далі встановимо перемикач типу задання нижньої основи у положення «Сторона» та введемо у поле введення під цим перемикачем значення «3». Введених параметрів цілком достатньо для автоматичного обчислення за програмою інших параметрів, необхідних для створення многогранника. Після натиснення кнопки «Створити» з'явиться вікно «Конструювання просторового об'єкту» з вкладинкою «Многогранник», де можна змінити (якщо потрібно) деякі параметри створюваного об'єкта. Після натиснення кнопки «Ок» модель піраміди буде створено: зображення п'ятикутної піраміди з'явиться у полі зображення головного вікна, а назва - у переліку об' єктів.
Далі треба створити об'єкт «Точка», що відповідає середині одного з бічних ребер піраміди. Для цього необхідно встановити просторові координати цієї точки, що не важко зробити, якщо відомі координати кінців ребра. Якщо підвести курсор мишки до будь-якої вершини піраміди на зображенні, у полі інформування з'являться просторові координати цієї вершини, у якій сходяться бічні ребра піраміди та координати будь-якої вершини, що належить основі. Встановивши перемикач типу об' єкта у положення «Точка», звернемося до послуги головного меню програми «Об'єкт/Створити». У вікні «Конструювання просторового об'єкта», що з'явиться, на вкладниці «Точка» введемо знайдені координати середини ребра, а у полі введення «Назва об'єкта» введемо «Середина бічного ребра». Після натискання «Ок» об'єкт буде створено.
Для задання площини перерізу зручно скористатися послугою програми «Об' єкт/Створити з екрану»: у полі зображення слід лише вказати три точки, що визначатимуть площину. Для цього потрібно послідовно підводимо курсор мишки на зображення точки «Середина бічного ребра» та на зображення вершин сторони основи піраміди, протилежної до вибраного бічного ребра. У вікні «Конструювання просторового об' єкта», що з' явиться після вказання третьої точки, на вкладці «Площина» введемо назву об' єкта «Площина перерізу» та натиснемо «Ок».
Залишилося лише виконати операцію перерізу піраміди площиною. Для цього доцільно скористатися послугою програми «Операції/Виконати переріз» та за відповідними запитами програми у полі зображення. За допомогою мишки вказати площину перерізу та многогранник, стосовно якого виконується операція. Після виконання операції у полі з' явиться результат обчислення площі та периметра утвореного перерізу, а також буде створено два нових об'єкти-многогранники: «Ч. 1. Правильна п'ятикутна піраміда» та «Ч. 2. Правильна п'ятикутна піраміда», що є частинами базової піраміди в різних півпросторах відносно площини перерізу. Надалі утвореними об'єктами можна оперувати як окремими моделями. Для унаочнення моделей стереометричних тіл доцільно скористатися послугою програми «Зображення/Режим півтонового зображення», завдяки чому об'єкти зображуються з врахуванням видимості ліній і площин, чим досягається «реалістичність» зображення.
Функційональні можливості ППЗ GRAN-3D дозволяють учням добудовувати та видозмінювати моделі та повертатися до попередніх ракурсів відповідно, чим значно підвищується ефективність навчання. Адже аналізуючи динамічні моделі, встановлюючи суттєві зв'язки між її складовими, виділяючи певні ознаки, учні активізують розумову діяльність.
Слід зауважити, що можливості використання розглядуваного програмного засобу не обмежується розв' язуванням задач наведеного типу.
Додаткова інформація програми GRAN-3D про площі та периметри окремих граней многогранників (послуга Обчислення/Многогранник/Площі та периметри граней) дає змогу проводити розрахункові експерименти з порівняння об' єктів за загальними і спеціальними ознаками 1-о рівняння зображень можна здійснювати одночасно з експериментуванням з відповідними розрахунками параметрів просторових моделей. Це збагачує фактологічну базу для співставлення та протиставлення об'єктів, для вибору інваріантної ознаки основи систематизації. Аналіз моделей полегшує поділ об'єктів, що належать обсягу поняття «многогранник» на моделі типу «призми» і типу «не призми», тобто надає можливість учням краще засвоїти основні принципи процесу класифікації математичних об' єктів. Даний програмний продукт не може бути використаний на всіх етапах уроку і під час вивчення будь-якого навчального матеріалу. Для підтримки шкільного курсу стереометрії запроваджено в навчальний процес пакет ППЗ «STEREO», розроблений Моторіною В. Г. [3]. Даний пакет складається з 8 програм і використовується під час вивчення розділів «Многогранники», «Тіла обертання», «Об'єми многогранників», «Об'єми і площі поверхонь тіл обертання» в курсі стереометрії 11 класу. Для кожної з тем виділено два типи програм: програми для актуалізації знань учнів з даної теми, програми для навчання учнів розв' язуванню задач.
У ППЗ «STEREO» передбачено аналіз помилок учня, допущених у процесі виконання завдань, що є важливою дидиктичною вимогою особистісно-орієнтованої концепції побудови сучасної освіти, а саме дає змогу учню одразу здійснити «ліквідацію» прогалин у навчальному матеріалі.
Отримання міцних знань, повноцінний розвиток учнів неможливий без систематичного, добре організованого контролю і за процесом засвоєння, і за результатами навчання. У кожному випадку перевага у використанні програмного пакету «STEREO» оцевидна, оскільки: дозволяє проводити ефективне управління процесом навчання; підвищує рівень знань та сформованості умінь і навичок; сприяє глибокому усвідомленню суті геометричних понять, які вивчаються в курсі стереометрії; активізує дослідницький, творчий підхід до розв' язування стереометричних задач.
Одним з найвідоміших ППЗ є GeoGebra ― вільно-поширюване динамічне геометричне середовище, що об'єднує в собі геометрію, алгебру та арифметику. Даний програмний продукт був створений під керівництвом Маркуса Хохенвартера, роботу над яким він розпочав у 2001 році на базі Зальцбурзького університету та продовжив в Університеті Флорида Атлантік (2006-2008), Університеті штату Флорида (2008-2009 роки), і тепер в університеті в Лінці. Розроблене програмне забезпечення розраховане для викладання та вивчення математики у середніх школах та коледжах (10-18 років), проте воно надає широкі можливості для застосування і у вищій школі.
На відміну від інших програм для динамічного маніпулювання геометричними об'єктами, ідея GeoGebra полягає в інтерактивному поєднанні геометричного, алгебраїчного і числового подання.
Програма надає багаті можливостями для роботи з функціями (побудова графіків, обчислення коренів, екстремумів, інтегралів і т. д.). Однією із значних її переваг є можливість покроково відображати хід побудови фігур. Таким чином, є можливість анімовано змінювати координати точок, тоді фігура ніби оживає на моніторі, змінюючи своє зображення внаслідок зміни координат опорних точок.
GeoGebra має інтуїтивно-зрозумілий інтерфейс, що складається з вікна графіки та вікна алгебри, і не потребує значних зусиль для засвоєння. З одного боку, у вікні графіки, користувач за допомогою миші може створювати будь-які геометричні побудови за допомогою точок, векторів, прямих, дуг тощо, алгебраїчне подання яких відобразиться у вікні алгебри. З іншого боку, координати та рівняння об' єктів можуть бути введені за допомогою клавіатури у вікні алгебри, тобто існує безпосередній зв' язок алгебри з геометрією. Таким чином, можна легко складати графіки функцій, працювати зі слайдерами для підбору необхідних параметрів.
Наведемо приклад використання динамічного пакету на практиці.
Задача.
Точки
P,
Q
і R
взяті на поверхні паралелепіпеда
 наступним
чином: точка Р лежить на діагоналі
наступним
чином: точка Р лежить на діагоналі
 ,
точкаR
―
на ребрі
,
точкаR
―
на ребрі
 ,
а точкаQ
―
на ребрі
,
а точкаQ
―
на ребрі
 .
Побудуємо переріз паралелепіпеда
площиноюPQR.
.
Побудуємо переріз паралелепіпеда
площиноюPQR.
Розв’язання. 1-ий крок. У динамічному середовищі GeoGebra будуємо і наносимо на полотно всі дані з умови задачі (рис. а).Користуємося інструментами з головної панелі, на якій знаходимо прямі, відрізки, точки та всі необхідні деталі для побудови макета паралелепіпеда.

Рис.а)
2-
ий крок.
Будуємо пряму XY,
по якій перетинаються площини PQR
і ABC,
тобто слід січної площини ABC.
Для цього будуємо точку Х
― точку перетину прямих RQ
і
 і точку Y
― точку
перетину прямих PQ
і
і точку Y
― точку
перетину прямих PQ
і
 (рис.
б).
(рис.
б).

Рис. б)
3-
ій крок.
Тепер, використовуючи знайдений слід
XY,
побудуємоточку
S,
в якій січна площина перетинає пряму
 .
Оскільки точкаS
лежить
на прямій
.
Оскільки точкаS
лежить
на прямій
 ,
то точка
,
то точка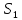 ―проекція
точки
S
на площину АВС
співпадає з точкою
C.
Знаходимо точку
V
― точку перетину прямих
―проекція
точки
S
на площину АВС
співпадає з точкою
C.
Знаходимо точку
V
― точку перетину прямих
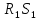 іXY.
Оскільки точки R
і
V
лежать в січній площині і в площині
грані
іXY.
Оскільки точки R
і
V
лежать в січній площині і в площині
грані
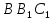 ,
то пряма
RV
― це лінія перетину вказаних площин, і
тоді точка S
― це точка перетину прямих RV
і
,
то пряма
RV
― це лінія перетину вказаних площин, і
тоді точка S
― це точка перетину прямих RV
і
 .
Аналогічно знаходимо точку
Z
як точку перетину прямих
.
Аналогічно знаходимо точку
Z
як точку перетину прямих
 і
XY,
а за тим точку T
― точку перетину прямих ZQ
і
і
XY,
а за тим точку T
― точку перетину прямих ZQ
і
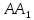 .
З’єднуємо далі точкуT
з точкою
R,
отримуємо точку E
на ребрі
.
З’єднуємо далі точкуT
з точкою
R,
отримуємо точку E
на ребрі
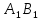 .
В площині
.
В площині ми отримуємо точки
F
і
E,
які лежать також і в січній площині.
Тоді ці площини перетинаються по прямій
FE,
причому, оскільки, точка P
також належить і площині
ми отримуємо точки
F
і
E,
які лежать також і в січній площині.
Тоді ці площини перетинаються по прямій
FE,
причому, оскільки, точка P
також належить і площині
 ,
і січній площині, то прямаFE
пройде через точку
P
(рис.
в)
,
і січній площині, то прямаFE
пройде через точку
P
(рис.
в)

Рис. в)
4 – ий крок. З’єднуємо знайдені точки прямими та одержуємо шуканий переріз QFERS (рис. г).
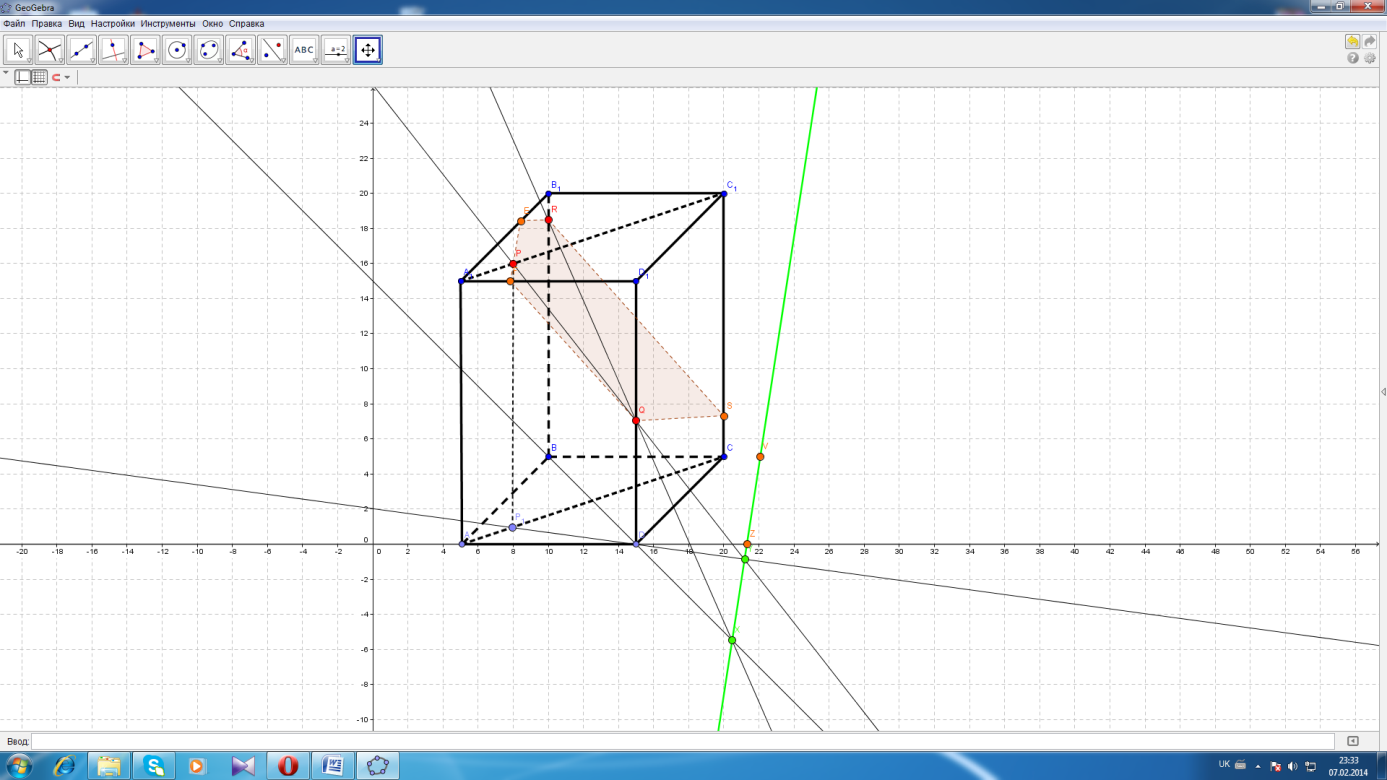
Рис. г)
5-ий крок. На данному прикладі дуже зручно показати учням як буде змінюватися переріз та розміщення сліду в залежності від розташування точок на ребрах. І зауважити, що не кожного разу доцільно використовувати метод слідів, оскільки бувають випадки, коли слід знаходиться на дуже великій відстані і це не зручно для вирішення завдання.
У чинній програмі з математики зазначено: «Підвищенню ефективності уроків математики в старших класах сприяє використання програмних засобів навчального призначення. Широке й системне застосування методу математичного моделювання протягом вивчення курсу математики може стати потужним засобом формування в учнів навички повсякденного користування математикою при вивченні природничих предметів».
Алгоритми побудов у СДГ — повчальні й цікаві для учнів. Віртуальні лінійка (відрізок, промінь, пряма) і циркулі (у фіксованій площині — коло, у просторі — сфера) дозволяють застосовувати всі класичні алгоритми задач на побудову.
Побудови — складова частина розв'язування. За допомогою методів паралельного проектування вони зводяться до плоского малюнка на площині, що відображає ракурс зображення просторового геометричного тіла. У разі необхідності його зміна потребує часу на уроці і тому рідко виконується. Виготовити фізичну тривимірну модель до кожної стереометричної задачі також неможливо. Окрім того, статичні моделі не дозволяють варіювати параметри, отже, не сприяють дослідженням. Динамічні малюнки, що легко й миттєво змінюються, створюють СДГ, середовища інтерактивного моделювання у віртуальному просторі, просторового конструювання. Кожний малюнок у ньому є фактично нескінченною множиною малюнків. Учень може зафіксувати той один, на якому він уявляє дану конфігурацію найкраще.
Найважливіше те, що малюнок у СДГ — це модель, яка зберігає не лише результат побудови, а також її алгоритм з усіма кроками, вихідними даними, залежностями між базовими об' єктами. Усі поточні побудови фіксуються й за необхідності легко редагуються. Будь-які зміни в необхідному масштабі й динаміці відображаються на дисплеї. Отже, роль малюнка зростає суттєво. Він стає не лише ілюстрацією у процесі розв'язування, а його важливою й невід'ємною частиною.
«Провідним принципом, який визначає структуру навчання математики за математичним та фізико-математичним профілями, є моделювання в навчальному процесі елементів діяльності фахівця-математика», — наголошується в програмі з математики. Вважаємо, що систематичне використання програмних засобів навчального призначення сформує в учнів навички їх застосування в процесі навчання у вузі, розширить математичний кругозір, познайомить з методами дослідження у відповідній галузі науки.
Наведемо практично значимі аспекти застосування СДГ Cabri 3D.
Детально моделювання стереометричних динамічних конфігурацій з досвіду викладання геометрії розглянуто в роботах [22; 23].
• Наочна демонстрація аксіом, означень, теорем, доведень. Комп'ютерні моделі чудово виконують роль інтерпретаторів математичних тверджень. Говорячи, що означений кут між площинами не залежить від вибору січної площини, що міра двогранного кута не залежить від вибору лінійного кута, доводячи задачу-теорему про об' єм похилої призми з виконанням паралельного перенесення її частини тощо, вчитель посилається або на статичні малюнки, або на уяву учнів. Засоби анімації, вбудовані в СДГ, дають можливість моделювати динаміку подібних процесів.
Учням варто наголосити, що в реальності ні точок, ні прямих, ні площин не існує. Узагалі, геометрія моделює і досліджує об'єкти в абстрактній формі. СДГ — це лише наочна й наближена комп'ютерна інтерпретація, яка перетворює стереометрію у красиву і «живу».
• Мимобіжні прямі. Ми виділяємо цей пункт тому, що на площині вказані об' єкти не існують, підручники і збірники задач містять недостатню кількість задач із цієї теми. Учням важко даються задачі на знаходження кутів і відстаней між мимобіжними прямими. Експериментування з моделями навчає їх знаходити і будувати необхідні паралельні площини, спільний перпендикуляр. Вважаємо, що СДГ дозволяють розглядати мимобіжні прямі пропедевтично значно раніше десятого класу.
Задача.
Дано
куб
 ,
довжина
ребра якого дорівнює а.
Знайти
довжини ребер тетраедра
,
довжина
ребра якого дорівнює а.
Знайти
довжини ребер тетраедра
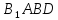 .
Для кожної пари мимобіжних його ребер
вказати паралельні площини, які проходять
через ці прямі або площину, що проходить
через одну з них, паралельно до другої.
Знайти відстань між мимобіжними прямими
першої, другої і третьої пари.
.
Для кожної пари мимобіжних його ребер
вказати паралельні площини, які проходять
через ці прямі або площину, що проходить
через одну з них, паралельно до другої.
Знайти відстань між мимобіжними прямими
першої, другої і третьої пари.
Подібні рівневі серії вправ доцільно пропонувати учням для розв'язування з
використанням
СДГ як навчальні. Шукані відстані:
 (рис. 3).
(рис. 3).
• Побудова перерізів. Ця тема — одна з найсприятливіших для вступу до моделювання. Рисунки нижче ілюструють відому задачу побудови перерізу куба площиною, яка проходить через три точки, що належать попарно мимобіжним ребрам.
Cabri
3D дозволяє виконувати реальні перерізи
(рис. 5) многогранників площиною
(Cut
Polyhedron),
довільно
маніпулювати многогранником
(Manipulation),
виконувати
анімацію
(Animation),
автоматично
і покроково відтворювати побудови
(Replay
Construction),
додавати
різні проекції для перегляду
(Document
/
Add
View
/ Front),
відтворювати
динамічні малюнки в
Microsoft
Word
тощо.