Рівень б

1. На полиці стоять 2 книжки з філософії, 4 з педагогіки і 3 – з математики. Навмання беруть одну книжку. Визначити ймовірність того, що взята книжка не з математики.

2. Ймовірність перемоги першого спортсмена дорівнює 0,7, другого – 0,8. Знайти ймовірність того, що хоча б однин з них переможе.

3. Між групою студентів із 30 осіб розподілили жеребкуванням путівки для відпочинку: 15 – в Крим, 8 – в Одесу, 7 – у Миргород. Яка ймовірність того, що два друга відпочинуть разом?

4. Студент шукає потрібну йому інформацію на трьох сайтах. Імовірність того, що інформація знаходиться на 1-му, 2-му і 3-тьому відповідно рівна 0,5; 0,7; 0,9. Знайти ймовірність того, що інформація міститься на всіх трьох сайтах.

5. Студент знає 21 із 26 питань програми. Знайти ймовірність того, що студент відповість на 3 питання, запропонованих йому викладачем.

6. Маємо два концентричні кола (мають спільний центр) радіуси яких відповідно рівні R=8, r =4. Знайти ймовірність того, що точка кинута навмання у більше коло не попаде у менше.

7. Три студенти складають іспит з психології. Ймовірність того, що перший складе іспит дорівнює 0,9, для другого – 0,8, для третього – 0,7. Обчислити ймовірність того, що два студенти складуть іспит.

8. Із множини чисел беруть навмання одне число, а потім з решти – друге. Яка ймовірність того, що здобуте двоцифрове число буде непарним?

9. Підприємство одержало 20 приймачів, з яких 5 бракованих. Для перевірки навмання взяли три приймача. Яка ймовірність того, що серед взятих приймачів буде один бракований?

10. На автомобілі встановлено два охороні пристрої, які працюють незалежно. Ймовірність того, що при викраденні спрацює переший дорівнює 0,85, другий – 0,95. Знайти ймовірність того, що при викраденні спрацює хоча б один.

Рівень в

1. Ймовірність того, що подія відбудеться хоча б один раз у трьох незалежних випробуваннях дорівнює 0,936. Знайти ймовірність появи події в одному випробуванні, якщо вона однакова у кожному.

2. Із великої зв’язки краваток, в якій краватки зеленого,, червоного і жовтого кольору перебувають у відношенні 5:3:2, двоє чоловіків навмання обирають по одній краватці. Яка ймовірність того, що вони оберуть краватки однакового кольору?

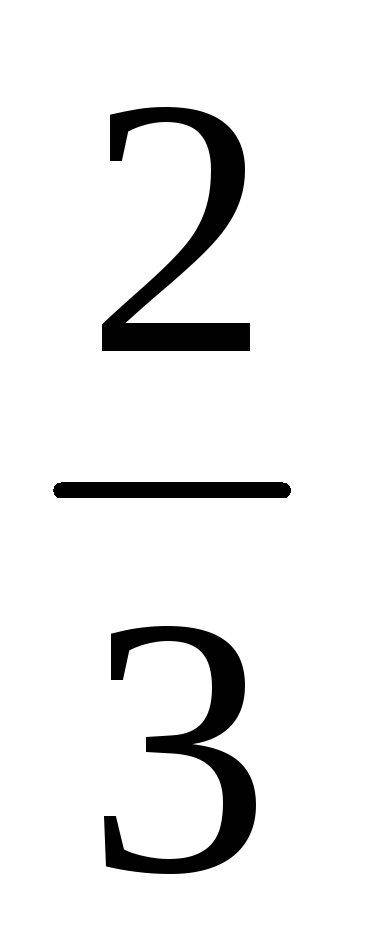3. Серед студентів п’ятого курсу одружені а решта неодружені. Серед неодружених студентівмолодші 22 років, аодружених старші 22 років. Знайти ймовірність того, що довільно обраний студент цього курсу старший 22 років.

4. У магазин надходять вироби, які виготовляються чотирма фабриками. Ймовірність браку виробів становить 0,04; 0,03; 0,06 і 0,02 відповідно. Від першої фабрики надійшло до магазину 30 виробів, від другої – 20, від третьої – 25, а від четвертої 25 виробів. Знайти ймовірність того, що взятий навмання виріб буде бракований.

5. До центру статистичних досліджень надходить інформація з трьох пунктів: з першого 50%, з другого – 30%, з третього – 20% усієї інформації. Ймовірність допущення помилки при обробці статистичних даних у першому пункті становить 0,1, у другому – 0,05, у третьому – 0,15. Яка ймовірність того, що отримана центром у даний момент часу достовірна інформація надійшла з другого пункту.

6. Ймовірність того, що таксофон відмовиться сприйняти вашу телефонну картку дорівнює 0,2, яка ймовірність того, що з 6 карток буде прийнято 4?

7. Спостереженнями встановлено, що у Полтаві у вересні в середньому буває 12 дощових днів. Яка ймовірність того, що серед навмання взятих у цьому місяці 8 днів три дні виявляться дощовими?

8. У лотереї на кожні 1000 білетів припадає один виграшний. Яка ймовірність того, що володар 200 білетів отримає два виграші.

9. Досліджують 500 проб залізної руди. Ймовірність того, що вміст заліза в ній достатній для промислового використання дорівнює 0,8. Знайти ймовірність того, що кількість таких проб буде від 300 до 400.

10. У перші класи передбачається прийняти 200 дітей. Визначити ймовірність того, що серед них буде 100 дівчат, якщо ймовірність народження хлопчиків у цьому році дорівнює 0,515.

IV. Тема реферату обирається студентом із числа запропонованих. Реферат повинен мати таку структуру: титульна сторінка, план, вступ, основна частина, висновки, список використаних джерел. В основній частині подати коротку біографічну довідку для вченого, але основну увагу приділити науковій діяльності вченого: вказати сфери його наукових досліджень, основні наукові праці, зупинитися на його особистому внеску в розвиток теорії ймовірностей як самостійної науки. Для теми № 15 визначити часові межі зародження теорії ймовірностей як самостійної науки. Виділити окремі етапи розвитку теорії ймовірностей. Окреслити сучасний стан розвитку теорії ймовірностей.