I.3. Профиль двухпирамидной системы Хеопса-Голода, дополненный золотым полу -эллипсом (рис. I.17)

Как известно (см. п.12.4.1., рис. 12. 37), равнобедренный треугольник про-филя пирамиды фараона Хеопса явля-ется индикатором золотого содержания эллипса, отношение длины большой полуоси оА которого к расстоянию от центра о до фокуса F выдержано в про-порции 1 : 0,618 и поэтому названного золотым.

Поэтому естественен интерес к ст-руктуре профиля двухпирамидной сис-темы Хеопса-Голода, дополненного зо-лотым полуэллипсом, описанным во-круг профиля пирамиды Хеопса.

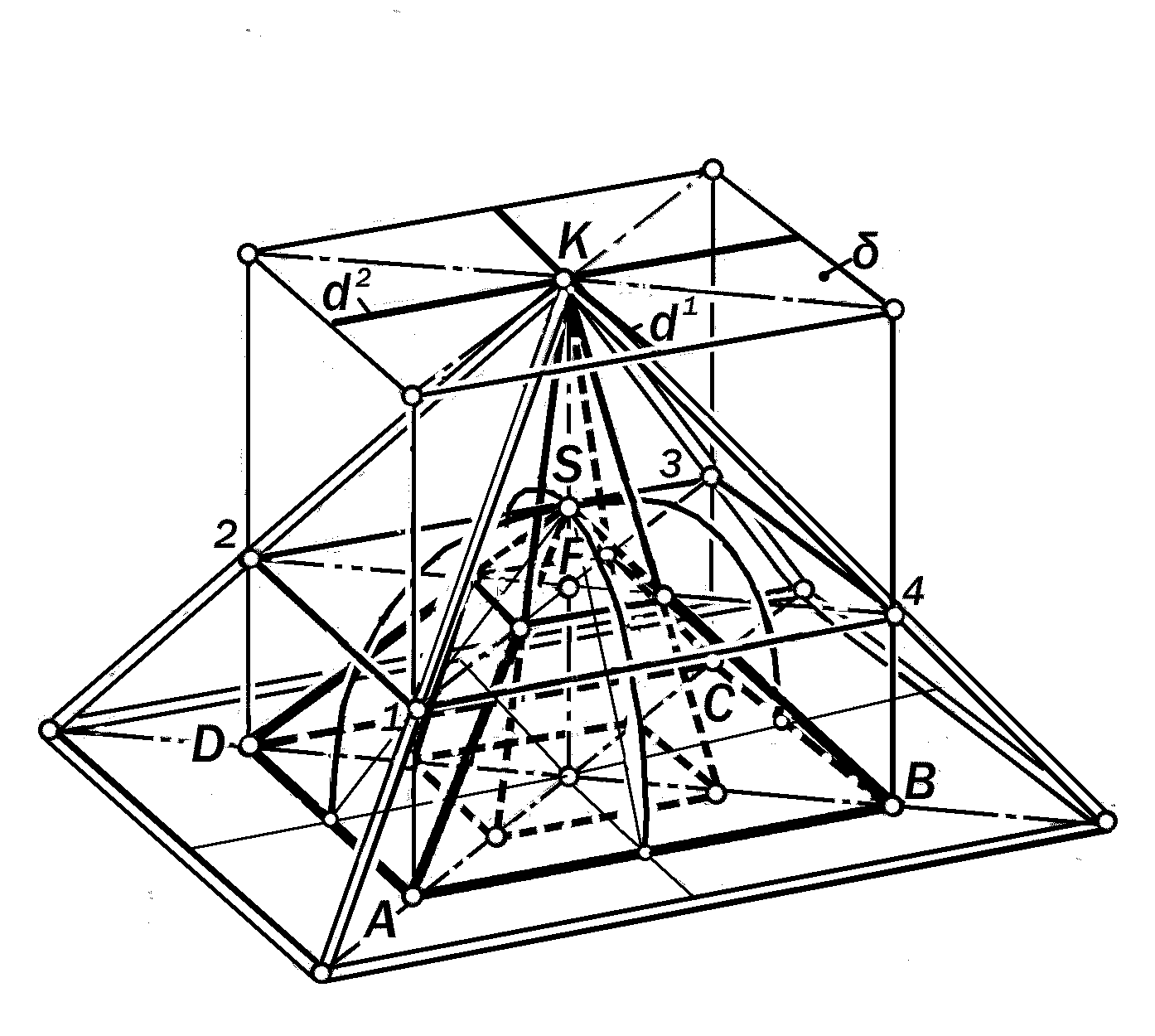
Из рис. 5.91 видно, что вершина К пирамиды Голода является основани-ем директрисы d¹ золотого эллипса а, описанного вокруг профиля пирамиды Хеопса. Но у пирамиды Хеопса два кон-груэнтных профиля, расположенных во взаимно-перпендикулярных плоскостях и поэтому через вершину пирамиды Голода проходят две директрисы d¹ и d², образующие горизонтальную дирек-трисную плоскость .

Так как основание К обеих дирек-трис графически определяется как точ-ка пересечения касательных 21К и 22К к окружности радиуса, равного большой полуоси оА эллипса а в концах её фо-кальной хорды, то концептуально воз-никает новый профиль МКN, подобный профилю ВАС пирамиды Хеопса. Сто-роны этого профиля изображают грани гипотетической габаритной пирамиды, подобной пирамиде Хеопса и содер-жащей изучаемую двухпирамидную си-стему (рис. I.17, I.18).

Рис. I.18. Общий вид габаритного куба и

пирамиды, подобной пирамиде Хеопса,

двухпирамидной системы Хеопса-Голода

Рис. I.19. Крестовый свод из поверхностей золотых эллиптических цилиндров, описанный вокруг пирамиды Хеопса

Рис. I.20. Золотой эллипсоид вращения с основанием, вписанным в основание пирамиды Хеопса

Рис. I.21. Крестовый свод , описанный вокруг пирамиды Голода.

Так как длина стороны квадратного основания пирамиды Хеопса равна вы-соте пирамиды Голода, то можно пред-положить, что существует габаритный кубический объём, верхней гранью ко-торого является директрисная плоско-сть , а плоскости боковых граней пе-ресекают грани габаритной пирамиды на уровне линии пересечения поверх-ностей исходных пирамид (см.рис. I.18).

I.4. Пространственная интерпрета-ция золотого полуэллипса в профи-ле двухпирамидной системы

Хеопса-Голода (рис. I.19- I. 22)

Линию фронтальной проекции зо-лотого полуэллипса можно представить двояко: как выроженную проекцию фро-нтально-проецирующей цилиндричес-кой поверхности и как очерк фронталь-ной проекции поверхности полуэллип-соида вращения.

Первое представление определяет возникновение вокруг пирамиды Хеоп-са крестового свода из двух поверх-ностей эллиптических цилиндров, нор-мальными сечениями которых являют-ся золотые полуэллипсы. Эти поверх-ности пересекаются по эллипсам, ко-торые принадлежат диагональным пло-скостям боковых рёбер пирамиды.

У каждой из этих поверхностей есть свои фокальные прямые, проходящие через общий фокус F во взаимно-пер-пендикулярных направлениях и свои взаимно-перпендикулярные директисы.

Второе представление определяет возникновение поверхности золотого полуэллипсоида вращения , основа-ние которого вписывается в квадратное основание пирамиды, а сама поверхно-сть пересекается гранями пирамиды по некоторым конгруэнтным эллипсам а, b, c, e, пересекающимся в её вершине.

Наличие эллиптических сечений пoверхности  вызывает наличие их фокусов и директрис, которые форми-руют свои фокальные и директрисные плоскости как конструктивные элемен-ты всей системы. На рис. I.20 фокаль-ные плоскости не показаны, а показана директрисная круговая плоскость  по-верхности  и квадратная плоскость ,

образуемая 4-мя верхними директри-сами «гранных» эллипсов а, b, c, e.

Описав крестовые своды и элли-псоиды вокруг пирамиды Хеопса, есте-ственно их описать и вокруг пирамиды Голода.

На рис. I.21 показан крестовый свод, образованный двумя цилиндри-ческими поверхностями, направляющи-ми линиями которых являются полу-эллипсы, описанные вокруг равнобед-ренного треугольника профиля пира-миды Голода. Эти полуэллипсы не яв-ляются золотыми, но они вписаны в двойные квадраты как основу построе-ния золотой пропорции.

Рис. I.22. Эллипсоид, образованный

вращением эллипса, описанного вокруг профиля пирамиды Голода

Отношение длины их малой оси в длине большой полуоси равно 2 к 4 или 1 к 2. Если рассмотреть диагональные треугольники АКС и ВКD, то длины ма-

лых полуосей описанных вокруг них эл-липсов относятся к длине их большой полуоси как  2 к 4 или 1,41 к 4, т.е., малая полуось укладывается в боль-шой 2,84 раза, что близко к пропорциям золотого равнобедренного треугольни-ка, у которого основание относится к высоте как 2 к 3.

Поверхность полуэллипсоида  , основание которого вписано в квадрат-ное основание пирамиды Голода, пере-секается её гранями по конгруэнтным эллипсам а, b, c, е, проходящим через вершину пирамиды и попарно пересе-кающимся на ее ребрах. Директрисы меридиональных и гранных эллипсов образуют свои директрисные плоскости

Рис. I.23. Двухкартинный комплексный чертёж системы «пирамида Хеопса-золотой эллипсоид» с разверткой боковой поверхности пирамиды