- •Глава 15. Геометрия ортогональных проекций кривых поверхностей
- •Принцип образования киноперспективных поверхностей изменяемой проекционной системой s – п
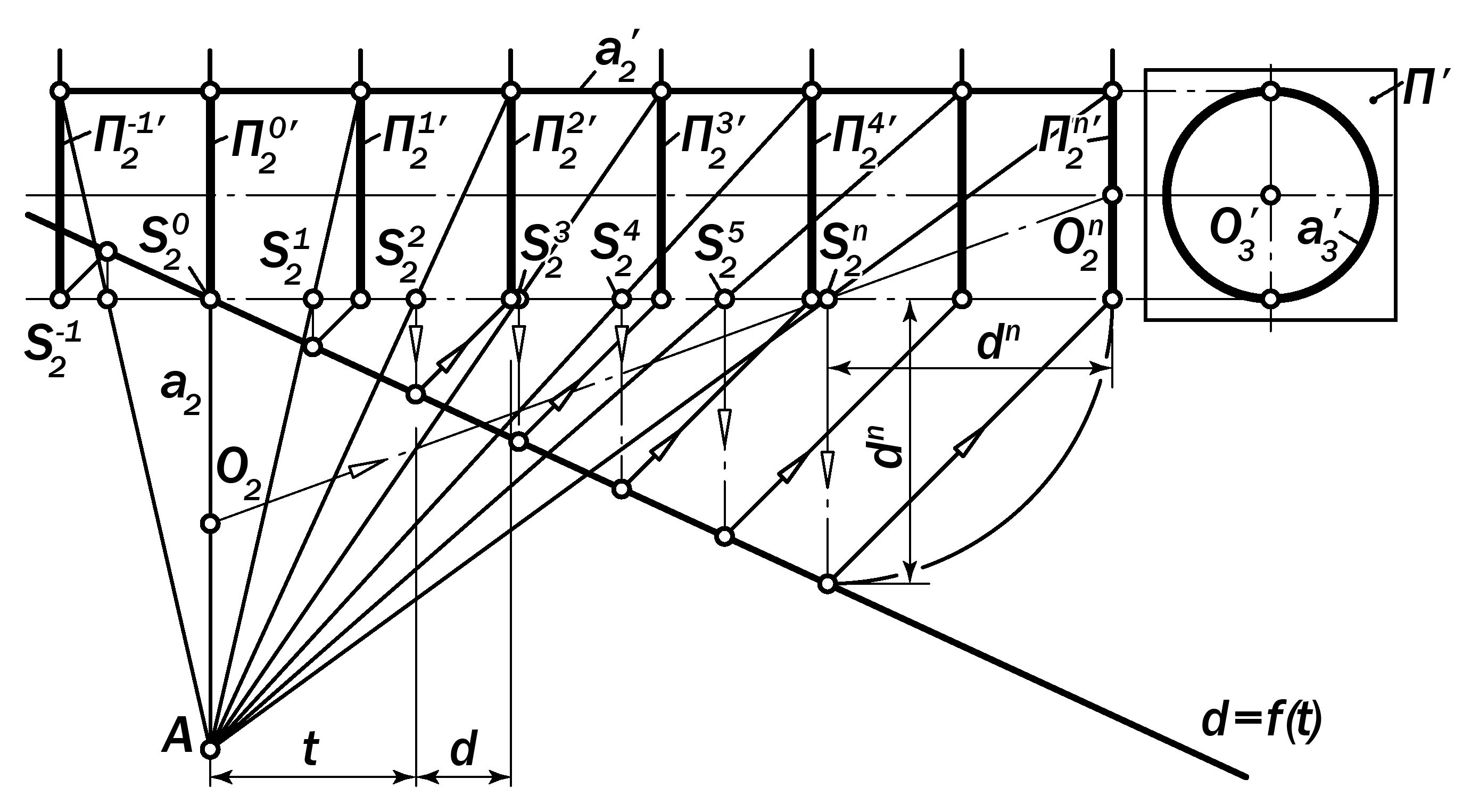
- •15.100. Геометрическая модель каналовой поверхности
- •15.2.6. Конструктивные свойства каналовых, трубчатых и циклических поверхностей и изобразительные свойства их ортогональных проекций
- •Конструктивные свойства каналовых поверхностей и изобразительные свойства их ортогональных проекций
- •Конструктивные свойства трубчатых поверхностей и изобразительные свойства их ортогональных проекций
- •Конструктивные свойства циклической поверхности и изобразительные свойства их ортогональных проекций
- •15.2.7. Конструктивные свойства графических поверхностей и изобразительные свойства их ортогональных проекций.
- •15.2.8. Конструктивные свойства топографических поверхностей и изобразительные свойства их ортогональных проекций
Глава 15. Геометрия ортогональных проекций кривых поверхностей
|
|
|
|
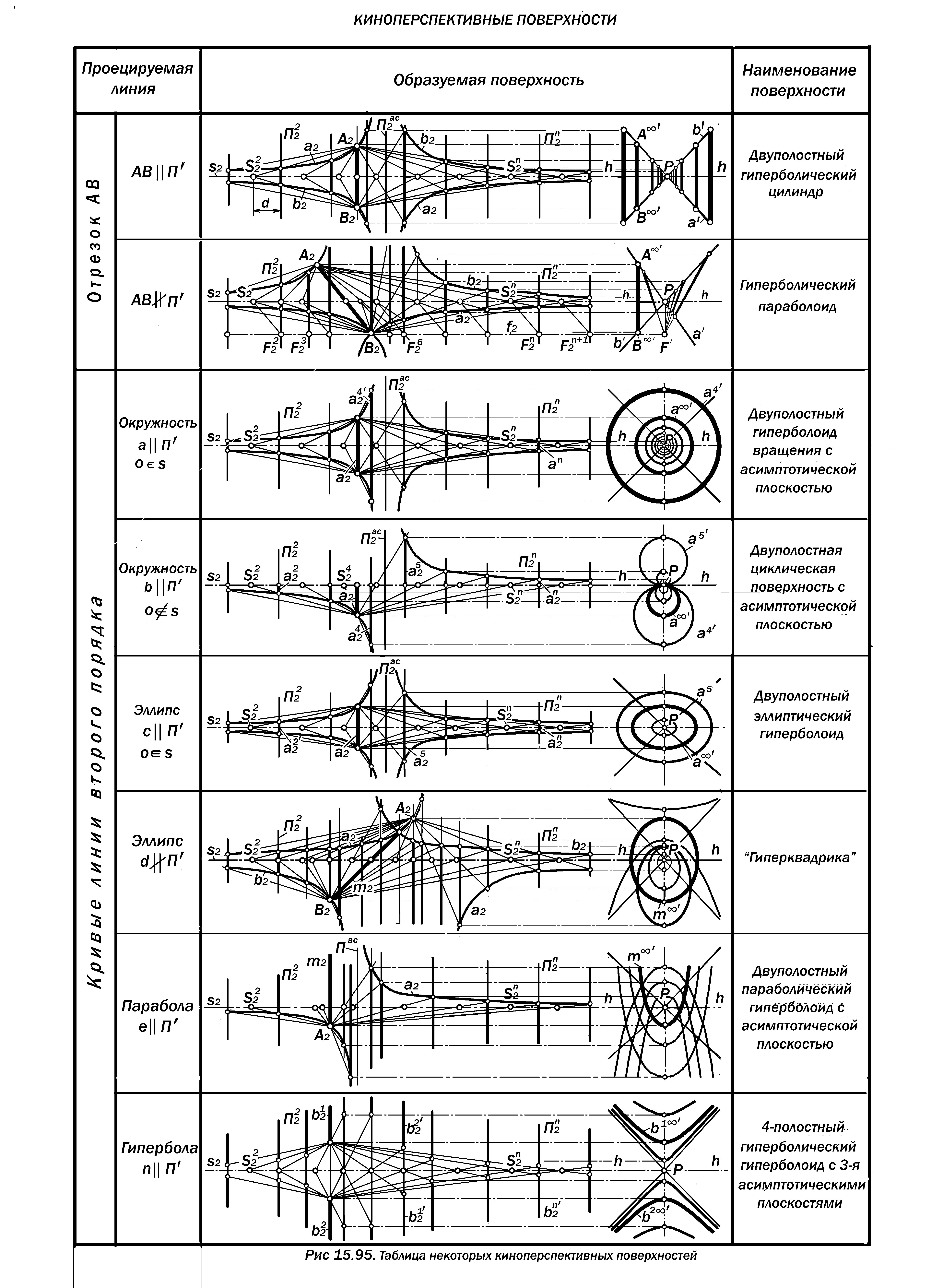
Анализ структуры поверхностей, получаемых неизменяемой проекцион-ной системой S – П ( рис.15.95 ), раскрывает их следующие конструктив-ные особенности:
1. все поверхности конструируются лучами специального линейного комп-лекса как однопараметрического мно-жества связок S, проецирующих линию а пространства R на соответствующие им картины П ;
2. Линейный каркас всех поверх-ностей формируется сетью меридиона-льных гипербол, инцидентных плоскос-тям пучка S, определяемым точками изображаемой линии а, и их паралле-лей как центральных проекций линии а на соответствующих положениях карти-ны. При этом точками проекций а яв-ляются точки пересечения лучей прое-цирующего комплекса с соответству-ющими лучами конгруэнтных пучков лучей Р, образующих в своей сово-купности ортогональную конгруэнцию прямых [ 27 ];
3. Гиперболичность всех поверхно-стей определяет наличие у них одной асимптотической оси – траектории дви-жения центра S и одной асимптотиче-ской плоскости, роль которой играет ка-
ртина, оказавшаяся в положении, па-
раллельном плоскости кривизны изобра-
жаемой линии и удалённом от неё на
главное расстояние системы S - П.
Одной из наиболее интересных яв-ляется поверхность, образуемая цен-тральным подвижным проецировани-ем эллипса z, плоскость кривизны кото-рого не параллельна подвижной карти-не (рис. 15.96). Она названа «гипер-квадрикой» потому, что её меридианы являются гиперболами, а в качестве параллелей выступает однопараметри-ческое множество эллипсов с различ-ными отношениями длин их большой и малой осей, две параболы, соответ-ствующие двум положениям центра, проецирующего вершины эллипса лу-чами, параллельными соответствую-щим картинам, конечное количество ги-пербол (по числу пар точек изобража-емого эллипса, проецируемых в бес-конечность), а также одной прямой ли-нии, в которую проецируется эллипс из центра S7 совпадающего с плоскостью его кривизны.
Полученная «человекообразная» по-верхность является своеобразным «ан-тиконусом», ибо её последовательные сечения параллельными картинами яв-ляются коническими. Это алгебраиче-ская поверхность 4-го порядка, так как произвольная прямая пересекает её максимум в 4-х точках.
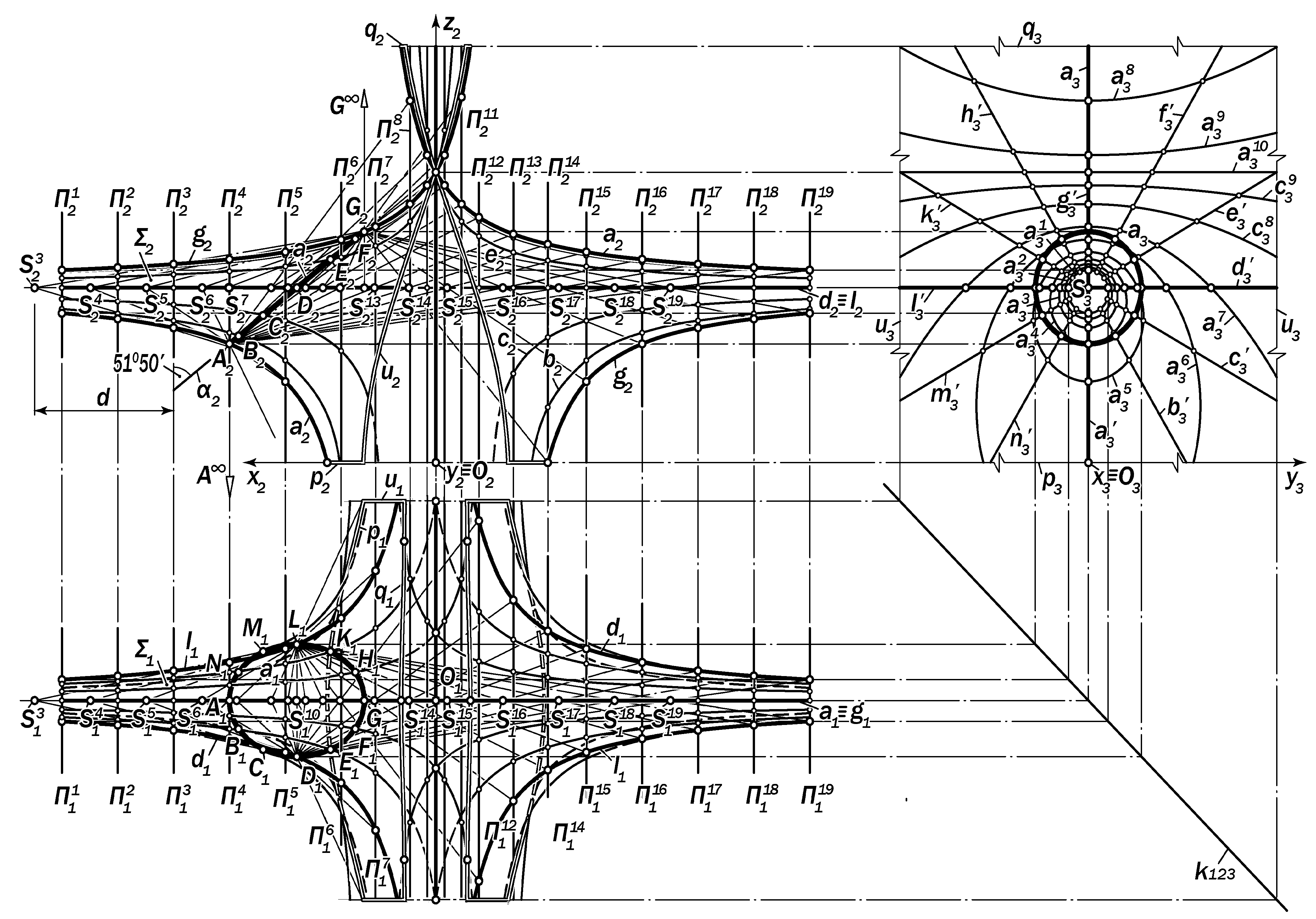
Изобразительные свойства ортогональных проекций гиперквадрики ( рис. 15. 97)
Начинать построение графической модели гиперквадрики следует с за-дания проекций изображаемого наклон-ного эллипса а (а1,а2,а3 ) П2, проекций профильно-проецирующей траектории s ( s1, s2 ) с необходимым и достаточ-ным количеством положений проециру-ющего центра S и таким же количест-вом положений картины П, сохраняю-щей в процессе движения центра пос-тоянное расстояние d с ним.
На рис.15.96 на эллипсе а взято 12
равномерно расположенных точек, ко-торые центральным подвижным прое-цированием преобразуются в гипербо-лы, плоскости кривизны которых, буду-чи перпендикулярными к П3, проециру-
ются на неё в пучок прямых с центром в точке s3 Р.
|
|
гиперквадрики
Если все точки эллипса а проециру-ются в гиперболы, то центральные про-екции самого эллипса как параллели поверхности , выглядят различными кривыми линиями 2-го порядка. Если картинная плоскость пересекает все лу-чи проецирующей данный эллипс ко-нической поверхности, то он изобража-ется эллипсом, если центр S занимает положения S7 и S13, проецирующие кон-цы большой оси АG эллипса а лучами, параллельными картинам П7, П13 в бес-конечность, то проекцией эллипса а на на эти положения картины будут в данном случае две конгруэнтные пара-болы а37 и а313.
Если центр S занимает положения, проецирующие в бесконечность по две точки эллипса, то его точки, располо-женные за нейтральной плоскостью, проецируются в одну ветвь гиперболы, а точки перед этой плоскостью,- во вто-рую её ветвь. Таких гипербольных про-екций эллипса будут столько, сколько центр будет занимать положений, из ко-
торых пары точек эллипса а будет про-ецироваться в бесконечность.
Если в своём движении центр S со-впадает в плоскостью кривизны эллип-
са а, то связка S10 проецирующих лучей преобразовалась в плоский пучок, кото-рый спроецировал его точки на картину П10 в прямолинейный точечный ряд а10 как вырожденную центральную проек-цию эллипса а. В точках этого ряда пе-ресекаются соответственные меридио-нальные гиперболы как киноперспек-тивные проекции точек эллипса а, фор-мируя верхнюю полу поверхности . Линейный каркас этой полы дополняет-ся верхними ветвями гипербольных проекций эллипса а. В итоге очерк фронтальной проекции 2 гиперквад-рики становится «человекообраз-ным», симметричным относительно ве-ртикальной оси.
Очерком её горизонтальной проек-ции являются 4 ветви равнобоких ги-пербол, сопряженных относительно 2-х взаимно-перпендиулярных асимптот – проекции s1 траектории s движения центра и вертикальной оси симметрии всей проекции.
В состав профильной проекции по-
верхности входят центральные проек-ции эллипса а на последовательных положениях картины в натуральном ви-де.
|
|
Так как по своей природе эта по-верхность простирается в бесконечно-сть по всем трём направлениям, то на рис 15.97 она ограничена фигурами сечений тремя парами плоскостей уро-вня.
Следует отметить, что на этом ри- сунке изображена только собственно кривая поверхность. Полное представ-ление о её структуре может быть полу-чено после построения директрисных и асимптотных поверхностей фигур её сечений картинными плоскостями.