Окремі випадки розподілу Гіббса:

а) розподіл молекул по швидкостям (закон Максвелла)

(2.36)

де N – кількість молекул, відносні швидкості яких лежать в інтервалі від u до u + u; – відносна швидкість, – швидкість молекули і

–найбільш імовірна швидкість молекул;

N – загальне число молекул;

При розв’язуванні задач на розподіл молекул по швидкостям зручно використовувати таблицю (1)

Таблиця 2.1

U		U		U
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8	0 0,02 0,09 0,18 0,31 0,44 0,57 0,68 0,76	0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7	0,81 0,83 0,82 0,78 0,71 0,63 0,54 0,46 0,36	1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5	0,29 0,22 0,16 0,12 0,09 0,06 0,04 0,03

б) барометрична формула (у припущенні, що температура в усіх точках однакова) дає залежність тиску газу від висоти h в полі сили тяжіння

(2.37)

де – тиск на висоті h = 0; g – прискорення сили тяжіння.

Рівняння стану реального газу (рівняння Ван-дер-Ваальса) для одного моля

(2.38)

де – об’єм моля; a і b – постійні, які залежать від природи газу.

Рівняння для будь-якої кількості газу

(2.39)

Постійні a і b зв’язані з критичними параметрами співвідношеннями

(2.40)

Властивості рідини.

Коефіцієнт поверхневого натягу рідини

або (2.41)

де F – сила поверхневого натягу, яка діє на контур довжиною l, що обмежує поверхню рідини; W – енергія, яку треба затратити для збільшення площі поверхні на величину S.

Формула Лапласа для додаткового тиску, викликаного кривиною поверхні рідини

(2.42)

де і- радіуси кривини двох взаємно перпендикулярних перерізів поверхні рідини. Радіус вважається додатним, якщо меніск опуклий і від’ємним, якщо меніск угнутий.

Висота підняття рідини у капілярі

(2.43)

де r – радіус капіляра;  - густина рідини;  - крайовий кут. При повному змочуванні  = 0, при повному незмочуванні  = 180.

Приклади розв’язання задач Приклад 1. Знайти густину кисню при нормальних умовах.

Розв’язання

Застосуємо рівняння Менделєєва – Клапейрона (2.3)

(1)

де P – тиск газу, V – об’єм газу; m – маса газу; M – молярна маса газу; R – газова постійна; T – термодинамічна температура.

Густина речовини

(2)

Розв’язуємо сумісно (1) і (2). Для цього з (2) виразимо m і підставимо в (1)

або

звідки

Перевіримо одиницю вимірювання

Підставимо числові дані.

При нормальних умовах P = 760 мм. рт. ст. , T = 0 С = 273К;

R = 8,31 Дж / (моль  K), M = .

Відповідь

Приклад2. Скільки молекул міститься у посудині ємністю 5л, заповненому вуглекислим газом? Температура у посудині 127 С, тиск 0,1 МПа.

Розв’язання

Кількість молекул ,

де  – кількість речовини; – постійна Авогадро.

Кількість речовини  знайдемо, скориставшись рівнянням Менделєєва – Клапейрона (2.3)

де P – тиск газу, V – об’єм газу; R – газова постійна;

T – термодинамічна температура.

Тоді

Перевіримо одиницю вимірювання.

(безрозмірна величина).

Підставимо числові дані, виразивши їх в системі Сі

Т = 127 + 273 = 400К

Відповідь

Приклад 3. У балоні об’ємом 5л міститься гелій під тиском 2МПа і температурі 127 С. Після того як з балону було взято деяку масу гелію, температура у балоні зменшилась на 10 градусів, а тиск зменшився до 1,5 МПа. Яку масу гелію було взято з балону?

Розв’язання

Скористаємось рівнянням Менделєєва – Клапейрона (2.3) записавши його для початкового і кінцевого станів газу у балоні.

(1)

(2)

де ,,– тиск, маса, термодинамічна температура у початковому стані;,,– відповідні величини у кінцевому стані; V – об’єм балону; – молярна маса гелію; R – газова постійна.

З (1) виразимо , з (2) виразимо.

Тоді

Перевіримо одиницю вимірювання

Знайдемо числове значення з урахуванням того, що

R = 8,31 Дж / (моль  K),

M = .

Відповідь = 2,77г.

Приклад 4. У посудині об’ємом V =25л міститься =100г гелію і=140г азоту при температур t =27. Знайти тиск у посудині.

Розв’язання

Скористаємося законом Дальтона (2.8), згідно з яким тиск у суміші газів дорівнює сумі парціальних тисків.

, (1)

де і(2)

і - малярні маси гелію і азоту відповідно.

Підставимо (2) в (1).

Перевіримо одиницю вимірювання.

Обчислення.

Па

Відповідь:Р=2,99 МПа.

Приклад 5. Знайти густину ρ деякого газу, якщо тиск Р у балоні 380 мм рт. ст. , а середня квадратична швидкість руху його молекул =800м/с.

Розв’язання

Середня квадратична швидкість теплового руху молекул газу за формулою (2.16) дорівнює

, (1)

де ; Т – абсолютна температура; M– молярна маса газу.

Звідки . (2)

Порівняємо з рівнянням Менделєєва-Клапейрона

(3)

З (2) виразимо і підставимо в (3):

, або (4)

За визначенням густина ρ= m/V, тому з (4)

ρ. (5)

Перевіримо одиницю вимірювання.

[ρ].

Переведемо тиск у одиницю вимірювання в системі :

P=380 мм рт. ст. 133 = 0,5Па.

Підставимо у (5) числові дані

ρкг/.

Відповідь: ρ=0,23 кг/.

Приклад 6. Визначити середню довжину вільного пробігу молекул азоту при нормальних умовах, а також середнє число зіткненьмолекули за одну секунду при даних умовах.

Розв’язання

Середню довжину вільного пробігу молекул можна визначити за допомогою співвідношення (2.17):

де - ефективний діаметр молекули. Із таблиць визначаємо, що для азоту=м;

n – концентрація молекул при даних умовах.

Концентрація молекул можна зв’язати з параметрами стану газу за допомогою рівняння (2.13):

P = nkT, звідки , (2)

де Р – тиск газу; Т – термодинамічна температура; k – постійна Больцмана.

Підставимо (2) у (1)

. (3)

Перевіримо одиницю вимірювання

.

Для нормальних умов Т=273 К і Р=Па, k=Дж/К.

Обчислення.

=м.

Середнє число зіткнень кожної молекули за 1 сек. можна визначити за формулою (2.18).

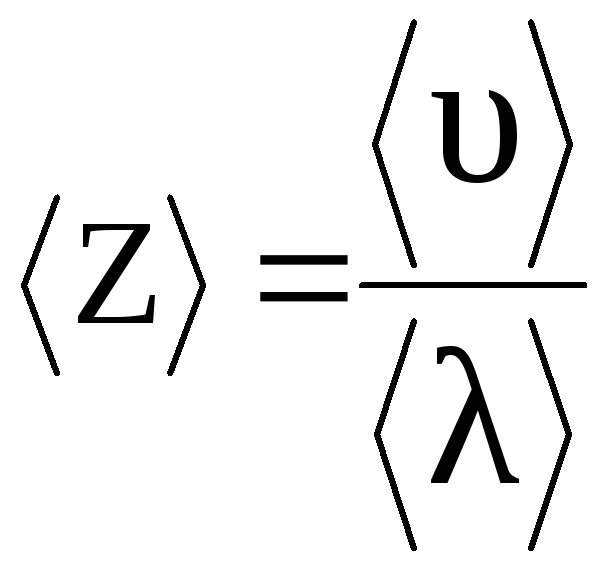, (4)

де - середня арифметична швидкість теплового руху молекул;- середня довжина вільного пробігу молекул, яку вже визначено за формулою (3).

Середню арифметичну швидкість молекул знайдемо за допомогою формули (2.15).

м/с.

Підставимо значення іу (4)

.

Відповідь: м;.

Приклад 7. Знайти енергію W обертального руху молекул, які містяться у =2 кг водню при температурі t=27.

Розв’язання

Кількість молекул, які містяться у даній масі газу, згідно з (2.2)

, (1)

де - кількість речовини, а- постійна Авогадро.

У свою чергу , де M – малярна маса.

Тоді . (2)

Так як молекула водню складається з двох атомів і має між ними жорсткий зв'язок, кількість ступенів свободи для такої молекули i=5 з них 2 припадає на обертальний рух: i=2. Середня кінетична енергія однієї молекули (2.12)

, (3)

де k – постійна Больцмана; Т – термодинамічна температура.

Тоді загальна енергія обертального руху всіх молекул

, або .

Так як , де k – газова постійна,

. (4)

Перевіримо одиницю вимірювання

.

Підставимо числові дані, зважаючи на те, що i=2; М=кг/моль; Т=27+273=300 К; R=8,31Дж/.

Дж.

Відповідь: W= Дж.

Приклад 8. Вуглекислий газ масою m=66г, який має температуру t=, ізотермічно розширюється так, що його об’єм збільшується вдвічі. Яку роботу виконує при цьому газ?

Розв’язання

Роботу, яку виконує газ, можна знайти, скориставшись формулою (2.24):

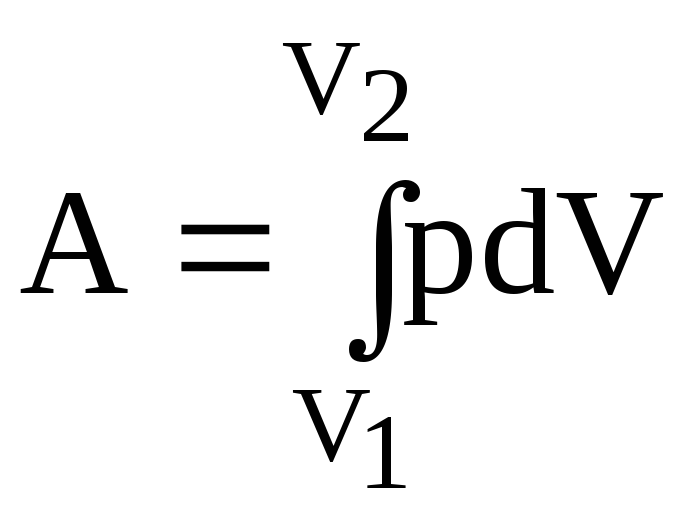. (1)

Так як під час ізотермічного процесу тиск Р теж змінюється, виразимо тиск через об’єм газу з рівняння Менделєєва – Клапейрона (2.3):

, звідки . (2)

Підставимо (2) у (1) і виконаємо інтегрування:

. (3)

Зважаючи на те , що =m/M, маємо

.

Перевіримо одиницю вимірювання

.

З урахуванням того, що за умовою задачі і крім того

m=66г=кг;

Т=7+273=280К;

кг/моль.

одержимо

Дж=2,41 кДж.

Відповідь: А=2,41 кДж.

Приклад 9. При ізобаричному нагріванні m=6г водню з початковою температурою t=, його об’єм зріс у два рази (). Знайти: 1) роботу А газу; 2) зміну внутрішньої енергіїгазу; 3) кількість теплоти Q, яку надано газу.

Розв’язання

Робота газу при ізобаричному нагріванні (2.25):

.

Скористаємося рівнянням Менделєєва – Клапейрона, записавши його двічі: для початкового і кінцевого станів.

(1)

(2)

З (2) віднімаємо (1)

, або

. (3)

Різницю температур можна знайти з (2.26):

При Р=const ; за умовою задачі, тому. Тобто

К.

Тоді К.

Робота газу Дж =7,48 кДж.

Внутрішня енергія газу визначається за формулою (2.23).

,

Тоді зміна внутрішньої енергії , (4)

де i – кількість ступені свободи; для водню (двохатомна молекула) і=5.

Обчислення:

Дж = 18,68 кДж.

Згідно з першим началом термодинаміки (2.22)

Тому кДж.

Відповідь: А=7,48 кДж; =18,68 кДж; Q=26,16 кДж.

Приклад 10. Ідеальна теплова машина працює за циклом Карно. Температура нагрівача =400 К, охолоджувача=300 К. За кожен цикл машина отримує від нагрівача кількість теплоти=2,1 кДж. Визначити коефіцієнт корисної діїмашини і корисну роботу А, яку виконує машина за один цикл.

Розв’язання

Коефіцієнт корисної дії можна визначити або за формулою (2.29)

, (1)

або (для циклу Карно) за формулою (2.30)

(2)

Спочатку за формулою (2) знайдемо коефіцієнт корисної дії

.

Потім за формулою (1) знайдемо А.

=525 Дж.

Відповідь: =25%; А=525 Дж.

Приклад 11. m=10г водню ізобарично нагрівають від до. Знайти зміну ентропії газуу цьому процесі.

Розв’язання

Згідно з (2.31) зміна ентропії визначається за формулою

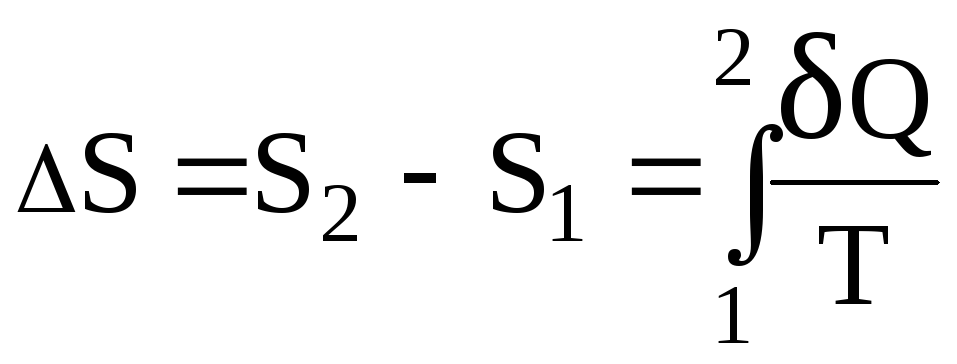, (1)

де і- значення ентропії відповідно у кінцевому і у початковому станах;- кількість теплоти, яку отримує газ у елементарному процесі; Т – термодинамічна температура, при якій відбувалась теплопередача.

При ізобаричному процесі

, (2)

де - молярна теплоємність водню при ізобаричному нагріванні;- кількість речовини; dT – збільшення температури.

У свою чергу

, (3)

де i – ступені свободи молекул (для водню i=5); R – газова стала. R=8,31.

, (4)

де m – маса газу; M– молярна маса газу. Для водню M=кг/моль.

Підставимо (2), (3), (4) у (1) і виконаємо інтегрування:

.

Виразимо температури іу кельвінах (К):

К; 327+273=600 К.

Обчислення.

100 Дж/К.

Відповідь: =100 Дж/К.

Приклад 12. Коефіцієнт внутрішнього тертя азоту при нормальних умовах дорівнює =1,78. Знайти коефіцієнт дифузії азоту D при цих умовах.

Розв’язання

Скористаємося формулами для коефіцієнтів D і (2.35):

(1)

(2)

де - середня арифметична теплового руху молекул;- середня довжина вільного пробігу молекул;- густина газу.

З порівняння (1) і (2) випливає, що

=D. (3)

Таким чином, для знаходження коефіцієнту дифузії азоту треба знайти його густину при нормальних умовах. З цією метою скористаємося рівнянням Менделєєва – Клапейрона (2.3):

(4)

За визначенням густина речовини =m/V, тому виразимо звідси m і підставимо у (4):

,

звідки . (5)

Тоді рівняння (3) з урахуванням співвідношення (5) має вигляд:

, звідки .

Перевіримо одиницю вимірювання.

Обчислення проводимо з урахуванням того що при нормальних умовах Р=760 мм рт. ст. = Па; Т=+273=273 К;

R=8,31 Дж/; M=28кг/моль.

Відповідь: В=1,44.

Приклад 13. Яка частина молекул азоту при температурі t=має швидкості від=300м/с до=310м/с?

Розв’язок

Розподіл молекул по швидкостям має вигляд (2.36):

, (1)

де – відносна швидкість. Вона дорівнює

де - швидкість молекули;- найбільш імовірна швидкість молекул. За формулою (2.16)

У нашому випадку

м/с.

Тоді, ;;;

і формула (1) дає:

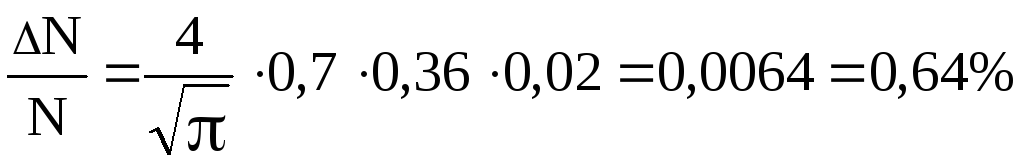
Відповідь: =0,64%.

Приклад 14. На якій висоті h атмосферний тиск Р складає 50% від тиску на рівні моря? Температуру вважати постійною і рівною t=, молярну масу для повітря вважати рівною M=0,029 кг/моль.

Розв’язання

Залежність атмосферного тиску від висоти над рівнем моря представлена барометричною формулою (2.37):

, (1)

де Р – тиск на висоті h; - тиск на рівні моря; M– молярна маса повітря; g=9,8- прискорення сили тяжіння; R=8,31 Дж/- газова постійна; Т – теплодинамічна температура.

Поділимо обидві частини рівняння (1) на Р:

, звідки .

За умовою задачі =2, тому. (2)

Логарифмуємо вираз (2): звідки

. (3)

Перевіримо одиницю вимірювання.

.

Підставимо у (3) числові дані:

м =5,53 км.

Відповідь: h=5,53 км.

Приклад 15. Дві краплині ртуті радіусом r=1 мм кожна, зливаються в одну. Скільки теплоти Q при цьому виділяється?

Розв’язання

Кількість теплоти Q дорівнює енергії , яка звільнюється тому, що зменшилося площа поверхні. Цю енергію можна знайти з формули (2.41):

, (1)

де - коефіцієнт поверхневого натягу ртуті;- площа, на яку зменшилась поверхня однієї краплі порівняно з площею поверхні двох попередніх.

, (2)

де r – радіус маленької краплі; R – радіус великої краплі.

Радіус великої краплі можна знайти з тих міркувань, що об’єм великої краплі повинен дорівнювати двом об’ємам малої краплі.

; звідки .

Підставимо у (2):

.

Тоді

.

Перевіримо одиницю вимірювання:

.

Коефіцієнт поверхневого натягу для ртуті знаходимо з таблиць.

=0,5 Н/м.

Обчислення.

Дж = 2,57 мкДж.

Відповідь: Q=2,57 мкДж.