Приклади розв’язання задач.

Приклад 1. Матеріальна точка рухається вздовж осі Ох за законом , де А=3 м, В=2 м/с, С=0,05 м/с. Визначити координату х, швидкість v й прискорення a у моменти часу;с, а також середні значення швидкостій прискоренняза перші 4 с руху.

Розв’язання.

Координати знаходимо підстановкою в рівняння руху числові значення коефіцієнтів А, В і С і часу t.

м; м=14,2 м.

Середня швидкість згідно (1.12)

м/с=2,8 м/с.

Миттєва швидкість відносно осі Ох є першою похідною від координати за часом (1.15):

.

Підставимо числові дані.

2 м/с; 4,4 м/с.

Середнє прискорення за (1.16)

м/с=0,6 м/с.

Миттєве прискорення за формулою (1.17)

=6Ct.

; м/с=1,2 м/с.

Відповідь: м; х= 14,2 м;2 м/с;4,4 м/с;;=1,2м/с;= 2,8 м/с;= 1,2 м/с.

Приклад 2. М’яч кинули з поверхні землі під кутом до горизонту із швидкістю= 10 м/с. Визначити висоту та дальність польоту. Обчислити нормальнета тангенціальнеприскорення черезс після початку руху.

Розв’язання.

Вибираємо систему координат ХОУ, початок якої О співпадає з точкою початку траєкторії руху тіла (Рис. 1.2). Розкладаємо початкову швидкість м’яча на 2 складові

; .

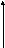
Рис. 1.2. Рис. 1.3.

Рух м’яча можна розглядати як суму двох незалежних рухів (горизонтального й вертикального). В горизонтальному напрямку на тіло не діють сили (якщо знехтувати опором повітря). Цей рух рівномірний і прямолінійний.

.

За формулою (1.22)

.

Вертикальний рух – це рух тіла, кинутого вертикально вверх, тобто рівнозміннний рух із прискоренням вільного падіння g = 9,8 м/с. За формулами (1.20) та (1.18) його описують рівняння

;

.

У верхній точці траєкторії вертикальна складова швидкості приймає нульове значення, після чого вертикальний рух із рівноуповільненого стає рівноприскореним.

Час польоту до верхньої точки траєкторії дістаємо з умови:

; .

Максимальна висота Н підйому

.

Час польоту м’яча до його падіння знайдемо з умови

,

; ,

тобто .

Дальність польоту

.

Для визначення ізображуємо швидкість і прискорення м’яча в даній точці траєкторії і розкладаємо вектори на складові (рис. 1.3). З трикутників, утворених векторами швидкості, прискорення з їх складовими, випливає:

, ,

де ;

= .

Підставляємо числові дані і проводимо обчислення.

Н=м = 2,55 м;м =10,2 м;

м/с= 2,87 м/с;

м/с= 9,36 м/с.

Відповідь: Н = 2,55 м; 10,2 м;= 2,87 м/с;= 9,36 м/с.

Приклад 3. Велосипедист повинен проїхати по замкненій петлі радіуса R = 3 м. З якої висоти він може скотитися, щоб не впасти? Тертям знехтувати.

Розв’язання.

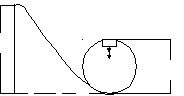
На тіло в верхній точці петлі діють дві сили, спрямовані вертикально вниз: сила тяжіння и реакція опори. (Рис. 1.4). Вони надають тілу нормальне (доцентрове)

Рис. 1.4. прискорення (1.8):

.

За другим законом Ньютона (1.42)

.

У проекції на напрямок прискорення, з урахуванням виразу для нього, отримуємо .

Таким чином, щоб не впасти велосипедист повинен мати швидкість, при якій задовольняється умова

, або .

Необхідну швидкість велосипедист набуває, скотившись із гірки висотою Н. За законом збереження механічної енергії (1.81) його повна енергія на початку руху дорівнює повній енергіїу верхній точці петлі.

; .

З попередньої нерівності отримуємо

.

Звідки .

м.

Відповідь: м.

Приклад 4. Порожиста сталева кулька підіймається з глибини води h = 400 м на поверхню. Швидкість установленого руху кульки v´ = 1,2 м/с. На яку відстань і в якому напрямі відхилиться кулька? Широта місцевості φ= 60°.

Розв’язання.

Рух кульки розглядатимемо у системі відліку, яка зв’язана із Землею. На кульку діють чотири сили: гравітаційна , відцентрова, виштовхуюча (архімедова)та коріолісова. Векторна сума перших трьох сил визначає рух по вертикалі для заданого місця Землі. За умовою їх рівнодіюча дорівнює нулю, внаслідок чого рух кульки по вертикалі – рівномірний.

Сила Коріоліса (1.65)

Рис.1.5.

перпендикулярна до площини, в якій лежать вектори і, її напрямок визначається за правилом правого гвинта. В даному випадку вона перпендикулярна до площини рисунка і напрямлена на нас (рис. 1.5).

,

де v´– швидкість, з якою кулька рухається відносно Землі; – кутова швидкість обертання Землі; період обертання Т = 24 год. = 8,64·с;– широта місцевості.

Сила надає кульці в горизонтальному напрямі на захід постійне прискорення.

За формулою шляху при рівноприскореному русі (1.19) знаходимо, що зміщення на захід кульки за час підйому дорівнює

Перевіряємо одиницю вимірювання

.

Підставляємо значення величин у формулу

9,69

Відповідь: s = 9,69 м.

Приклад 5. На спокійній воді озера стоїть човен довжиною L= 3м і масою M= 180 кг. На кормі човна стоїть людина масою m = 60 кг. На яку відстань s відносно берега переміститься човен, якщо людина перейде з корми на ніс човна?

Розв’язання.

Задачу вирішуємо у системі відліку, пов'язаною з берегом.

Припустимо для простоти, що людина йде відносно човна з постійною швидкістю . Тоді й човен буде рухатися рівномірно, і його переміщення s відносно берега дорівнює

, (1)

де v – швидкість човна відносно берега, t – час руху людини й човна.

За законом збереження імпульсу (1.67), оскільки на початку човен – нерухомий,

,

де - швидкість людини відносно берега.

У проекції на напрямок руху людини останнє рівняння має вид:

.

Звідки для швидкості човна отримуємо

. (2)

Час руху човна дорівнює часу руху людини вздовж човна, тобто

. (3)

Підставляємо отримані для v і t вирази (2) та (3) у формулу (1) і знаходимо переміщення човна.

.

Підставляємо в отриману формулу числові значення й обчислюємо s.

s = м = 0,75 м .

Відповідь: s = 0,75 м .

Приклад 6. Блок масою m = 1 кг закріплений наприкінці столу. Гирі однакової маси 1 кг з’єднані ниткою, яка перекинута через блок. Коефіцієнт тертя гирі 2 о стіл=0,1. Визначити прискорення а, з яким рухаються гирі. Блок вважати однорідним диском. Тертям у блоці та вагою нитки знехтувати.

Розв’язання.

Розглянемо рух тіл, що входять у систему та сили, які діють на них. Тіла 1 і 2 рухаються поступально, тіло 1 – вниз, тіло 2 – вправо. Блок обертається відносно горизонтальної осі, що проходить через точку О. На тіло діє сила тяжінняі сила натягу нитки. На тіло– сила тяжіння, сила натягу нитки, сила тертята сила реакції опору. На блок – сили натягу ниткиі. (Рис. 1.6.)

Рис. 1.6

Згідно ІІІ закону Ньютона = –,= –.

Кутове прискорення ε, з яким рухається блок, пов’язано з лінійним прискоренням а співвідношенням (1.38)

.

Момент інерції блока, який має форму диска (1.53). Сила тертя(1.46).

На підставі ІІ закону Ньютона (1.42) записуємо рівняння руху тіл ів проекції на напрямок руху. Рух блоку описує основне рівняння динаміки обертального руху (1.69), який записуємо у проекції на ось О

;

;

;

Після підстановки ε та І, з урахуванням виразу для сили тертя, отримуємо

;

;

.

Додаємо рівняння, що утворюють систему, один до одного і знаходимо прискорення

.

Підставляємо числові дані

м/с=3,53 м/с.

Відповідь: а = 3,53 м/с.

Приклад 7. В посудині з гліцерином падає свинцева кулька. Визначити максимальне значення діаметра кульки, при якому рух шарів гліцерину, спричинений рухом кульки, залишається ламінарним. В’язкість гліцерину η=1,0 Па·с.

Розв’язання.

Характер руху шарів рідини, який виникає завдяки силам внутрішнього тертя внаслідок руху тіла, визначається числом Рейнольдса Re ( 1.87). Якщо число Рейнольдса менше деякого критичного значення , рух рідини буде ламінарним, в протилежному випадку – турбулентним.

Якщо тіло, яке рухається в рідині, має форму кулі діаметром d, то

, (1)

де ρ – густина рідини (в нашому випадку ); η – коефіцієнт внутрішнього тертя рідини; v – швидкість руху кульки.

При цьому критичне значення числа = 0,5.

Виразимо швидкість кульки, розглянувши сили, які діють на неї у процесі руху. На кульку діють три сили:

1) сила тяжіння кульки (1.44)

,

де – густина свинцю, V – об’єм кульки;

2) виштовхуюча сила , яка визначається за законом Архімеда (1.82),

,

де – густина гліцерину;

3) сила внутрішнього тертя , яка визначається формулою Стокса (1.86),

.

При установленому русі кульки в рідині (v=const) сила тяжіння урівноважується сумою виштовхуючої сили та сили внутрішнього тертя,

тобто =+,

звідки . (2)

Сумісний розв’язок рівнянь (1) і (2) відносно d, дає

.

Максимальне значення діаметра кульки відповідає критичному значенню числа Рейнольда. Тому

.

Перевіряємо розмірність

.

Знаходимо з таблиці значення =1,26;=11,3.

Підставляємо значення величин в отриману формулу

.

Відповідь: м .