Теоретическая часть

1. ОСНОВНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.

Наиболее распространенной формулировкой задач линейного программирования (ЛП) является их представления в виде основной задачи линейного программирования (ОЗЛП). Эта задача звучит так: найти неотрицательные значения переменных x₁, x₂, …, x_n, которые обращали бы в максимум (или минимум) линейную функцию этих переменных

F(X) = c₁ x₁ +c₂ x₂ + . . . +c_n x_n ,

При ограничениях неравенствах:

a₁₁ x₁ +a₁₂ x₂ + . . . + a_1n x_n  b₁ ,

a₂₁ x₁ +a₂₂ x₂ + . . . + a_2nx_n  b₂ ,

… … … …

a_m1 x₁ +a_m2 x₂ + . . . + a_mn x_n  b_m .

При необходимости перехода от задачи максимизации к задаче минимизации целевой функции следует изменить знаки коэффициентовc_j при переменных x_j, на противоположные, т.е. задача максимизации функции F(X)=(C,X) приводится к задаче на поиск минимума функции -F(X)=(C,X).

Вектор X ={ x₁ , x₂, . . . , x_n } , удовлетворяющий ограничениям задачи ЛП, называется решением . При X  0 полученное решение называется допустимым. Если X обращает в максимум (минимум) целевую функцию F(X), то решение называется оптимальным.

2. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Графический метод основан на геометрической интерпретации задачи ЛП. Рассмотрим ограничения в виде равенств. Будем исходить из того, что число переменных n на два больше числа независимых уравнений ограничений m, т.е. n-m =2. Тогда две из переменных, например x₁ и x₂ можно принять в качестве свободных, а остальные m сделать базисными и выразить их через свободные. В результате получим m=n-2 уравнений вида:

x₃ = ₃₁ x₁ +₃₂ x₂ +₃ ,

x

()

₄ = ₄₁ x₁ +₄₂ x₂ +₄ ,

. . . . . . . . . . . . . . . . . ,

x_n = _n1 x₁ +_n2 x₂ +_n .

где _ij и _i  сочетания коэффициентов a_ij b_i соответственно.

Будем искать решение задачи на плоскости в прямоугольной системе координат x₁0x₂ (рис.1). Допустимые решения для переменных x₁ и x₂ будут находиться выше оси 0x₁ и правее.

Найдем на плоскости x₁0x₂ отображения остальных переменных x₃ , x₄ , . . . , x_n в соответствии с уравнениями (). С этой целью рассмотрим например переменную x₃ и положим, что ее величина равна своему крайнему значению, т.е. x₃ =0. Тогда из первого уравнения системы получим:

₃₁ x₁ +₃₂ x₂ +₃ =0 .

Это уравнение прямой на которой x₃ =0. Заштрихованная сторона этой прямой соответствует x₃ >0.

Аналогично строятся и остальные ограничивающие прямые x₄ =0, x₅ =0, . . . x_n =0, для каждой из которых определяется сторона, где x₁  0, x₂  0, . . . , x_n  0. Часть плоскости x₁0x₂ (заштрихованная область), называется областью допустимых решений (ОДР). В этой области значения всех переменных положительны. Вершины ОДР называются базисными допустимыми решениями.

Для нахождения оптимального решения подставим () в выражение для целевой функции и после приведения подобных членов получим

F(x)=₀ + ₁ x₁ + ₂ x₂

Запишем вместо F(x) функцию

F₁(x)= ₁ x₁ + ₂ x₂

Обе функции достигают максимума (минимума) при одних и тех же значениях переменных x₁ и x₂ .

Найдем значения x₁ и x₂ доставляющие максимум (минимум) функции F₁(x). Для этого определим положение этой функции на плоскости x₁0x₂, как показано на рисунке. При F₁(x)=0 эта функция есть прямая проходящая через начало координат. Вторая точка через которую пройдет эта прямая, определяется координатами x₁=₂, x₂=₁. Если функции F₁(x) придавать различные постоянные значения, то прямая на рисунке, отображающая эту функцию, будет перемещаться параллельно самой себе. Очевидно, максимального значения функция достигнет, когда прямая F₁(x) достигнет крайней точки С области допустимых решений.

3. ТАБЛИЧНЫЙ СИМПЛЕКС-МЕТОД

Оптимизационные исследования задач ЛП удобно проводить, пользуясь симплекс-таблицами. Существует достаточно большое количество форм симплекс-таблиц. Воспользуемся одной из форм, по которой рекомендуется следующий порядок решения задачи ЛП:

1. Математическая модель задачи приводится к расширенной форме.

2. Определяется начальное базисное допустимое решение.

3. Составляется исходная симплекс-таблица (табл. 4), в которую вносятся следующие параметры, соответствующие начальному базисному допустимому решению:

3.1. Весовые коэффициенты c_j при переменных x_j ( j=1, ... ,n) целевой функции (строка C).

3.2. Весовые коэффициенты c_j при базисных переменных x_i ( i=1, ... ,m) целевой функции (столбец C).

3.3. Переменные x_i ( i=1, ... ,m) , которые входят в текущий базис (столбец Х_р ).

3.4. Свободные коэффициенты b _i ( i=1, ... ,m) уравнений ограничений (столбец B).

3.5.Элементы a _ij ( i=1, ... ,m ; j=1, ... ,n) матрицы условий задачи (столбцы A₁, .., A_n ).

Таблица 4

C			c1	...	cj	...	ck	...	cn
	Хр	B	A1	...	Aj	...	Ak	...	An
c1	x1	b1	A11	...	a1j	...	a1k	...	a1n
...	...	...	...	...	...	...	...	...	...
ci	xi	bi	ai1	...	aij	...	aik	...	ain
...	...	...	...	...	...	...	...	...	...
cr	xr	br	ar1	...	arj	...	ark	...	arn
...	...	...	...	...	...	...	...	...	...
cm	xm	bm	am1	...	amj	...	amk	...	amn
S			S1	...	Sj	...	Sk	...	Sn

3.6. Оценки S_j ( j=1, ... ,n) векторов условий A_j , которые определяются по формуле :

где c_i  весовые коэффициенты при базисных переменных .

Из этой формулы следует, что коэффициенты z _j вычисляются для каждого столбца как сумма почленных произведений коэффициентов c_i на одноименные коэффициенты j-_го столбца. При заполнении симплекс-таблицы (в дальнейшем будем рассматривать задачу максимизации целевой функции) необходимо иметь в виду:

 если S_j  0 для всех j=1, ..., n, то полученное решение является оптимальным;

 если имеются S_j <0 и в столбцах A_j, соответствующих этим отрицательным оценкам, существует хотя бы один элемент a_ij > 0, то возможен переход к новому решению, связанному с большим значением целевой функции;

 если имеются S_k <0 и в столбце A_k все элементы a_ik  0, то в области допустимых решений целевая функция не ограничена сверху.

4. Определяется вектор A_k, который необходимо ввести в базис для улучшения решения, по наибольшему значению _k . Переменная этого столбца x_k будет новой базисной переменной, которая вводится в базис. Столбец, содержащий эту переменную, называется направляющим столбцом.

5. Определяется вектор, который нужно вывести из базиса, используя равенство:

Это условие позволяет найти направляющую строку. Переменная x_r, соответствующая этой строке, выводится из базисного решения и заменяется переменной x_k направляющего столбца. Элемент a_rk, который стоит на пересечении направляющего столбца и направляющей строки, называется направляющим элементом.

6. Заполняется таблица соответствующая новому базисному решению. В этой таблице, прежде всего заполняются клетки строки r с вводимой переменной x_k. Для этого все элементы этой строки делятся на направляющий элемент. Получаются элементы новой строки:

Остальные элементы новой таблицы определяются по формулам исключения (на основании метода полного исключения Гаусса):

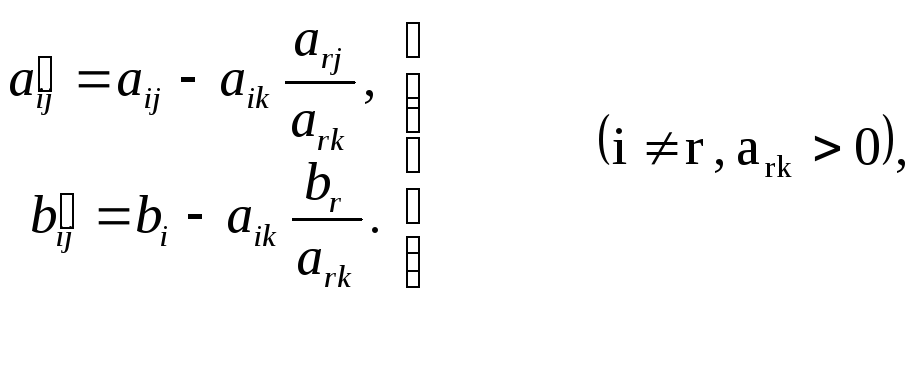
Процесс вычислений заканчивается, когда найдено оптимальное решение.