5. Квадратичное программирование

Квадратичное программирование позволяет проводить оптимизационные исследования в задачах, в которых целевая функция составлена из линейных и квадратичных слагаемых, а ограничения являются линейными функциями. Задача квадратичного программирования представляет собой случай общей задачи нелинейного программирования.

Модель задачи квадратичного программирования имеет следующую структуру:

найти максимальное (минимальное) значение функции

при ограничениях

Второе слагаемое в выражении (*) называется квадратичной формой переменных х₁, х₂, …, х_n и представляются в виде:

Матрицакоэффициентов квадратичной формы предполагается симметричной(d_kj = d_jk). Диагональные элементы d_kk этой матрицы являются коэффициентами при , а недиагональные элементы(d_kj = d_jk) равны половине коэффициента при x_kx_j

Можно использовать следующий порядок нахождения решения решения задачи квадратичного программирования:

1. Составляется функция Логранжа.

2. Записываются условия для ограничений.

3. Используется метод искусственного базиса с применением математической модели.

4. Находится оптимальное решение при выполнении условий п. (2).

Расчетная часть

ЗАДАЧА 1

Целевая функция F(x)=2x₁ + 4x₂  max;

при ограничениях :

Для приведения к положительным правым частям умножаем необходимые ограничения на (-1) и записываем в виде:

Приведём ограничения к расширенной форме, при этом если знак неравенства , то базисная переменная входит в уравнение с положительным знаком. Если знак неравенства, то переменная входит в уравнение с отрицательным знаком:

Неравенства ограничений приведем к равенствам, используя дополнительные переменные x ₃ , x ₄ и x ₅ :

х₁, х₂ – свободные переменные.

х₃, х₄, х₅ – базисные переменные.

Выразим систему ограничений относительно базисных переменных и приравняем полученные уравнения к нулю:

где x _1, x _2, x _3, x _4, x ₅ >0

переменные x ₃ , x ₄ и x ₅ примем в качестве базисных и выразим через свободные x ₁ и x ₂

Прямые, соответствующие граничным значениям переменных x₃ = x₄ = x₅= 0 представлены на рис. 2. Заштрихованная область будет областью допустимых решений.

Рис.2

Максимального значения целевая функция достигает в крайней точке A области допустимых решений. Координаты точки A будут оптимальным решением задачи:

ЗАДАЧА 2

Решить задачу методом симплекс - таблиц.

Целевая функция F(x)= – 2x₁+2x₂  min;

Уравнения ограничения

Так как целевую функцию необходимо исследовать на минимум, то для удобства умножим ее на –1, и она будет выглядеть следующим образом:

F(x)= 2x₁–2x₂  max

Запишем уравнения ограничения в расширенной форме:

4x₁ + 7x₂ + x₃ = 28 ,

x₁ + x₂ +x₄ = 6 ,

–3x₁ + 2x₂  x₅ +x₆ = 3 ,

x₁ , x₂  0 .

Целевая функция примет вид: F(x)= 2x₁–2x₂ +0x₃ +0x₄ +0x₅ Mx₆ max , где M.

Обозначим векторы условий задачи через A₁  A₆ . Векторы A₃ , A₄ , A₆ образуют единичную матрицу, которую примем за базис. В результате начальное базисное допустимое решение будет иметь вид X(0,0,28,6,0,3).

Составим исходную симплекс-таблицу (табл.6), в которой рассчитаем элементы строки S.

Таблица 6

C			c1 2	c2 –2	c3 0	c4 0	c5 0	c6 M
	ХP	B	A1	A2	A3	A4	A5	A6
c3 0	x3	28	4	7	1	0	0	0
c4 0	x5	6	1	1	0	1	0	0
c6 M	x6	3	–3	2	0	0	1	1
S		3M	23M	–2+M	0	0	–M	0

В индексной строке табл.6 имеются S_j > 0, что позволяет улучшить решение задачи.

Вводим в новый базис вектор A₂, которому соответствует наибольшее значение S₂ = 2 + M, а в новое базисное решение переменную x₂. Столбец, содержащий вектор A₂ будет направляющим.

Составим отношения вида , по которым определим направляющую строку. Для этого находим:

Таким образом направляющая строка вторая, направляющий элемент a₂₂ (в таблице заключен в прямоугольник). Из базиса выводится вектор A₆ , а из базисного решения переменная x₆ .

Рассчитаем и заполним новую таблицу соответствующую новому базисному решению.

Таблица 7

C			c1 2	c2 –2	c3 0	c4 0	c5 0	c6 M
	ХP	B	A1	A2	A3	A4	A5	A6
c3 0	x3	35/2	29/2	0	1	0	7/2	-7/2
c4 0	x5	9/2	5/2	0	0	1	1/2	-1/2
с2 2	х2	3/2	–3/2	1	0	0	1/2	1/2
S		3	23M	0	0	0	–1	1– M

В таблице все S_j  0. Поэтому полученное решение является оптимальным:

ЗАДАЧА 3

Решить транспортную задачу .

_{3 5}

Целевая функция F =   c _ij x_ij;

^{i=1 j=1}

Условия транспортной задачи представлены в табл. 8

Табл.8

ПП ПО	В1	В2	В3	В4	В5	Запасы
А1	5	2	10	10	6	80
А2	6	4	3	9	2	80
А3	8	9	7	8	4	40
Заявки	40	30	30	40	60

Определим опорный план, используя правило “северо-западного угла”.

Результаты сведены в табл. 9.

Таблица 9

5 40	2 30	10 10	10	6	80
6	4	3 20	9 40	2 20	80
8	9	7	8	4 40	40
40	30	30	40	60

Таким образом опорный план имеет вид:

Полученное решение являетсяопорным (начальным базисным допустимым решением), в котором переменные имеют значения: х₁₁=40; х₁₂=30; х₁₃=10; х₂₃=20; х₂₄=40; х₂₅=20; х₃₅= 40.

Стоимость полученного плана найдем, умножив каждую перевозку на соответствующую стоимость: F = 40*5 + 30*2 + 10*10 + 20*3 + 40*9 + 20*2 + 40*4 = = 980.

Находим значения потенциалов u_i и v_j , соответствующие базисным клеткам, принимая для удобства u₁=0.

u₁ + v₁ =5; u₁ = 0, v₁ = 5;

u₁ + v₂ =2; v₂ = 2;

u₁ +v₃ = 10; v₃ = 10;

u₂ + v₃ = 3; u₂ =7;

u₂ + v₄ = 9; v₄ = 16;

u₂ + v₅ = 2; v₅ = 9;

u₃ +v₅ = 4; u₃ = -5.

Находим для небазисных клеток оценки с учетом значений потенциалов u_i и v_j:

Так как среди оценок имеются положительные, то план можно улучшить, осуществляя перевозки по замкнутому циклу. Начальная вершина цикла соответствует небазисной клетке с наибольшей положительной оценкой(). Таким образом перевозки осуществляем по следующему циклу x₁₄  x₂₄  x₂₃  x₁₃.

Полученные результаты представим в табл. 10.

Таблица10

ui\vj	5	2	10	16	9
0	5 40	2 30	10 10	6 10	3 6	80
-7	-8 6	-9 4	3 20	9 40	2 20	80
-5	-8 8	-12 9	-2 7	3 8	4 40	40
	40	30	30	40	60	bj\ai

Новый опорный план:

Проверим на вырожденность опорный план m+n-1=6. Опорный план не вырожден.

Стоимость полученного плана найдем умножив каждую перевозку на соответствующую стоимость:

F = 40*5 + 30*2 + 10*10 + 30*3 + 30*9 + 20*2 + 40*4 = 920.

Находим значения потенциалов u_i и v_j , соответствующие базисным клеткам, принимая для удобства u₁=0.

u₁ + v₁ =5; u₁ = 0, v₁ = 5;

u₁ + v₂ =2; v₂ = 2;

u₁ +v₄ = 10; v₄ = 10;

u₂ + v₃ = 3; v₃ = 4;

u₂ + v₄ = 9; u₂ = -1;

u₂ + v₅ = 2; v₅ = 3;

u₃ +v₅ = 4; u₃ = 1.

Находим для небазисных клеток оценки с учетом значений потенциалов u_i и v_j:

Так как среди оценок имеются положительные, то план можно улучшить осуществляя перевозки по замкнутому циклу. Начальная вершина цикла соответствует небазисной клетке с наибольшей положительной оценкой (). Таким образом перевозки осуществляем по следующему циклу x₃₄  x₃₅  x₂₅  x₂₄.

Полученные результаты представим в табл. 11.

Таблица 11

ui\vj	5	2	4	10	3
0	5 40	2 30	-6 10	10 10	-3 6	80
-1	-2 6	-3 4	3 20	9 40 -	2 20 +	80
-1	-2 8	-7 9	-2 7	3 8 +	4 40 -	40
	40	30	30	40	60	bj\ai

Новый опорный план:

Стоимость полученного плана найдем, умножив каждую перевозку на соответствующую стоимость:

F = 40*5 + 30*2 + 10*10 + 30*3 + 50*2 + 30*8 + 10*4 = 830.

Находим значения потенциалов u_i и v_j, соответствующие базисным клеткам, принимая для удобства u₁=0.

u₁ + v₁ =5; u₁ = 0, v₁ = 5;

u₁ + v₂ =2; v₂ = 2;

u₁ +v₄ = 10; v₄ = 10;

u₂ + v₃ = 3; v₃ = 7;

u₂ + v₅ = 2; u₂ = -4;

u₃ + v₄ = 8; u₃ = -2;

u₃ +v₅ = 4; v₅ = 6.

Находим для небазисных клеток оценки с учетом значений потенциалов u_i и v_j:

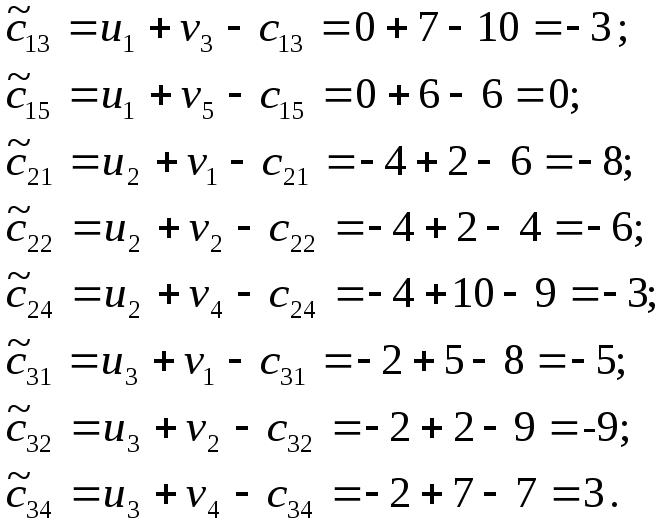
Так как все оценки для небазисных клеток отрицательны, то полученный план является оптимальным.

F^* = 40*5 + 30*2 + 10*10 + 30*3 + 50*2 + 30*8 + 10*4 = 830.

ЗАДАЧА 4

Решить задачу квадратичного программирования графически. Привести задачу к задаче линейного программирования специального вида. Решить задачу модифицированным методом искусственного базиса.

при ограничениях:

2х₁ + х₂  4;

- х₁ + х₂  2;

х1, х2  0.

Приведем задачу к задаче линейного программирования специального вида и решим модифицированным методом искусственного базиса.

Составим матрицу D и рассмотрим ее определители:

D =; ∆₁= -1 < 0

Составим функцию Лагранжа.

Запишем условие Куна - Таккера:

Систему линейных неравенств перепишем в виде:

2х₁ – 2х₂ + 2₁ - ₂  2

4х₂ – 2х₁ + ₁ + ₂  2

2х₁ + х₂  4

- х₁ + х₁  2

Получим систему линейных неравенств, т.е. задача приведена к задаче линейного программирования. Используя дополнительные переменныеv₁, v₂, w₁, w₂ приведем неравенства к равенствам.

2х₁ – 2х₂ + 2₁ - ₂ - v₁ = 2;

4х₂ – 2х₁ + ₁ + ₂ – v₂ = 2; (*)

2х₁ + х₂ + w₁ = 4;

- х₁ + х₁ + w₂ = 2;

Дополним равенства условиями, которые представим в виде:

v₁x₁ = 0; v₂x₂ = 0; w₁₁ = 0; w₂₂ = 0. (**)

Найдем базисное дополнительное решение системы (*) с учетом (**). Для этого воспользуемся методом искусственного базиса, вводя искусственные переменные z₁ и z₂.

Получим:

F(x) = -Mz₁ -M z₂

2х₁ – 2х₂ + 2₁ - ₂ - v₁ + z₁ = 2;

4х₂ – 2х₁ + ₁ + ₂ – v₂ + z₂ = 2;

2х₁ + х₂ + w₁ = 4;

- х₁ + х₁ + w₂ = 2;

Решим задачу методом симплекс-таблиц. Результаты показаны в табл. 12 - 15

Таблица 12

С			0	0	0	0	0	0	0	0	-M	-M
	XP	A0	Ax1	Ax2	A1	A2	Av1	Av2	Aw1	Aw2	Az1	Az2
-M	z1	2	2	-2	2	-1	-1	0	0	0	1	0
-M	z2	2	-2	4	1	1	0	-1	0	0	0	1
0	w1	4	2	1	0	0	0	0	1	0	0	0
0	w2	2	-1	1	0	0	0	0	0	1	0	0
S		-4M	0	2M	3M	0	-M	-M	0	0	0	0

Таблица 13

С			0	0	0	0	0	0	0	0	-M	-M
	XP	A0	Ax1	Ax2	A1	A2	Av1	Av2	Aw1	Aw2	Az1	Az2
0	1	1	1	-1	1	-1/2	-1/2	0	0	0	1/2	0
-M	z2	1	-3	5	0	3/2	1/2	-1	0	0	-1/2	1
0	w1	4	2	1	0	0	0	0	1	0	0	0
0	w2	2	-1	1	0	0	0	0	0	1	0	0
S		-M	-3M	5M	0	3/2M	1/2M	-M	0	0	-3/2M	0

Таблица 14

С			0	0	0	0	0	0	0	0	-M	-M
	XP	A0	Ax1	Ax2	A1	A2	Av1	Av2	Aw1	Aw2	Az1	Az2
0	1	6/5	2/5	0	1	-1/5	-2/5	-1/5	0	0	9/10	1/5
0	X2	1/5	-3/5	1	0	3/10	1/10	-1/5	0	0	-1/10	1/10
0	W1	19/5	13/5	0	0	-3/10	-1/10	1/5	1	0	1/10	-1/5
0	W2	6/5	-2/5	0	0	-3/10	-1/10	1/5	0	1	1/10	-1/5
S		0	0	0	0	0	0	0	0	0	-M	-M

В таблице 14 получено, предположительно оптимальное решение, но оно не отвечает условиям (**), следовательно, проделаем еще одну итерацию:

Табл. 15

С			0	0	0	0	0	0	0	0	-M	-M
	XP	A0	Ax1	Ax2	A1	A2	Av1	Av2	Aw1	Aw2	Az1	Az2
0	1	8/13	0	0	1				0	0
0	x2	14/13	0	1	0				3/13	0
0	x1	19/13	1	0	0				5/13	0
0	w2	64/65	0	0	0				2/13	1
S		0	0	0	0				0	0

Таким образом, получаем оптимальное решения, удовлетворяющее заданным условиям:

Для нахождения решения графическим методом, построим линии уровня исходной функцииF(x₁,x₂) и линии ограничения (ОДР) (рис.3).

Рис.3

На рис.3 видно, что значения

ЗАКЛЮЧЕНИЕ

В ходе выполнения расчётно-графической работы было проведено оптимизационное исследование задач линейного программирования, транспортной задачи по критерию стоимости, а также задачи квадратичного программирования. Для нахождения оптимальных решений в задачах линейного программирования был использован метод симплекс-таблиц, а также графическая интерпретация задачи линейного программирования. Для нахождения оптимального решения транспортной задачи по критерию стоимости был использован метод потенциалов, а начальное базисное допустимое решение (опорный план) было найдено с помощью правила минимального элемента. Поиск оптимального решения задачи квадратичного программирования происходил с применением множителей Лагранжа.

Полученные результаты:

ЗАДАЧА 1:

ЗАДАЧА 2:

ЗАДАЧА 3:

, F^* = 830.

ЗАДАЧА 4: