Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский национальный политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

MV1339.pdf

Скачиваний:

Добавлен:

10.02.2016

Размер:

529.51 Кб

Скачать

☆

<<< < Предыдущая 12 / 112 3 4 5 6 7 8 9 10 11 > Следующая >>>

Лабораторна робота № 1

Обчислювальні процеси що розгалужуються

1.1.Теоретична частина.

Будь-яка програма містить лінійні обчислювальні процеси.

У лінійних обчислювальних процесах всі операції виконуються послідовно одна за іншою в порядку їхнього запису. Це можливо при рішенні простих задач обчислення по формулах без всяких умов. У цих процесах використовуються найпростіші конструкції мови: слова, дані (константи, перемінні), арифметичні вираження, оператори.

При рішенні задач, що містять умови і варианты рішення виникає необхідність зміни порядок виконання операторів з метою одержання потрібного варіанта. Для цього використовують оператори умовного, безумовного переходу й оператори вибору.

Логічні вираження і оператори.

Логічне вираження (ЛВ) – це сукупність констант, перемінних, стандартних функцій, з'єднаних операціями відносини і логічними операціями. Їх використовують для перевірки умов в операторах умовного переходу.

Операціями відносини є: == (дорівнює); != (не дорівнює); > (більше); < (менше); <= ( менше чи дорівнює ); >= ( більше чи дорівнює); їх використовують

для порівняння значень АВ. Наприклад: x >y; a>=1; cos(х) <sin(x)-1. Це прості ЛВ. Їх називають відносинами. Результатом обчислення такого ЛВ є одне з логічних значень “істина” чи “неправда”.

До логічних операцій відносяться: логічне заперечення (!), операція логічного І (&&) і операція логічного ЧИ (!!). Операнды логічних операцій можуть бути цілого типу чи дійсного , при цьому в кожній операції можуть брати участь операнды різних типів. Наприклад: вираження (a > b) && (c < d) і (a > 1) !! (c < sin(x)) це складні ЛВ із двома відносинами.

Оператор умовного переходу використовується для переходу по однієї з двох галузей у залежності від виконання деякої умови (записаної у виді ЛВ). Повний формат оператора IF має вид

IF (ЛВ) Оператор1; ELSE Оператор2;

Де IF (якщо), ELSE (інакше) – ключові слова мови програмування Сі. Скорочений варіант оператора IF має вид

IF (ЛВ) Оператор;

Оператор IF у повному форматі спочатку обчислює значення ЛВ. Якщо результат True (істина), то виконується Оператор1, в противному випадку виконується Оператор2.

Приклад:

IF ( A == 0) && ( B != 0) z=x + y; ELSE z=x - y;

У даному прикладі (A == 0) && ( B != 0) – це складне ЛВ. Воно буде мати значення істина тільки в тому випадку, якщо одночасно виконувати дві умови A == 0 і B != 0. При

цьому буде виконаний оператор присвоювання z=x+y. Якщо хоча б одна з цих умов не виконана, то буде виконаний оператор присвоювання z=x-y;

Оператор IF у скороченому форматі теж обчислює значення ЛВ і якщо результат стина, то виконується Оператор, інакше цей оператор пропускається.

.2 Складений оператор.

Для того, щоб декілька операторів сприймалися в операторі IF як один оператор, з цих операторів фомують складений оператор.

Складений оператор – це сукупність декількох операторів, ув’язнених в операторні дужки { }. Наприклад,

IF (x < 1) { y = x ; z = -x;}; ELSE { y = -x; z = x; }

Приклад програми з операторм IF. Задача: Оючислити значення Y.

	x – 1,при x < 3
	Y=2x+1,при –3 < x< 3
	x2, при x > 3
На Сi програма буде мати вид:
# include <stdio.h>	/* Підключення стандартної бібліотеки введення-виводу */
main() {
float x,y;	/* Опис перемінних */
printf(“Уведіть значення х”); scanf(“%f”,&x); /* Уведення х */
if (x<=3) y=x-1; else if (x>3) y=xx+2; else y=2x+1;
printf(“При х = %f	y = %f”,x,y);
return 0; }

Оператор вибору варіанта.

При наявності в задачі декількох варіантів умов можна застосувати оператор вибору варіанта SWITCH. Його форма запису:

SWITCH (вираження)

{

CASE < SWITCH1 > : < оператор1 >; CASE < SWITCH2 > : < оператор2 >; CASE < SWITCH3 > : < оператор3 >; DEFAULT : <оператор>;

}

Де:

Вираження – вираження цілого, символьного типу; оператор – будь-який оператор мови Сi. Оператор може бути складеним. SWITCH – службове слово.

Оператор діє так:

Значення отриманого вираження порівнюється з константами оператора CASE. Виконується той оператор котрый соответсвует константі оператора CASE. Виконуються оператори які знаходяться нижче обраного оператора.

Якщо не виявлено не одного збігу то виконується оператор находящийся за оператором DEFAULT у випадку його наявності. (Оператор DEFAULT не обов'язковий).

Управління йде за структуру SWITCH.

Оператор BREAK . Щоб виконувати тільки ті оператори, які відповідають обраному номеру оператора CASE потрібно використовувати оператор BREAK, який забезпечує вихід з оператора SWITCH і передає управління за його межі.

Приклад програми з оператором SWITCH. Скласти програму, що по номеру функції i і значенню x обчислить одну з функцій 1 – sinx, 2 – cosx,

3 – tgx, 4 – lgx. Програма має вид:

#include <stdio.h> #include <math.h> main()

{

float x,y; int i;

printf("Уведіть значення x\n"); scanf("%f",&x);

printf("Уведіть номер функції\n"); scanf("%d",&i);

switch (i)

{

case 1:y=sin(x); break; case 2:y=cos(x); break; case 3:y=tan(x); break; case 4:y=log(x); break; default: printf("Помилка");

}

printf("При i=%d y=%f",i,y); return 0;

}

1.2. Запитання для контролю.

Як діє оператор IF у повній і скороченій формах запису? Що таке складений оператор?

Для чого призначений оператор SWITCH і як він записується? Які дані можна використовувати як селектор(вираження)?

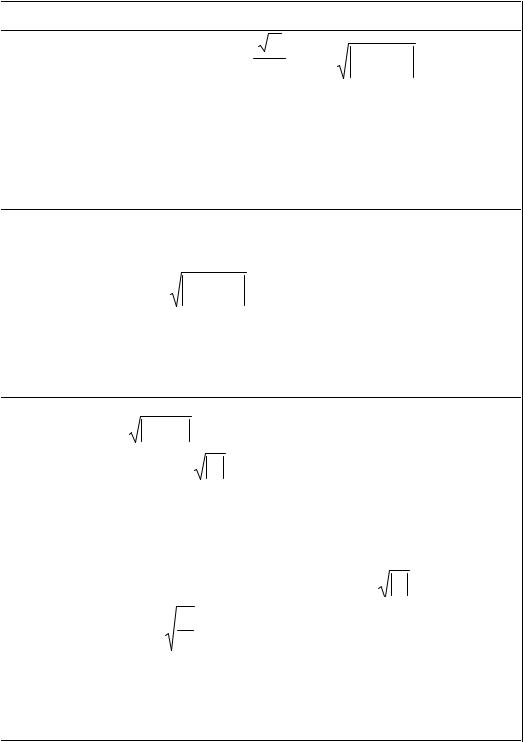
1.3. Завдання до лабораторної роботи № 1.

Обчислити значення перемінних по формулах

Q =

T =3 x2 + Z2

Z =sin

π)

;

5 Z

;

(a -1) ex

, якщо

;

S =

Q T

, якщо

Q2 <T ;

tg x2

, якщо Q2 =T ;

M =ln(x + y)+ c ;

N =

x2 −

; Q = M sin2x ;

4 c

x2 − y2

, якщо x <0 ;

R =

e2N

, якщо

x =0 ;

tg y2

, якщо

x >0 ;

B =

Z = 4 C + D ;

A = 4x - cos2D ;

C D ;

x -

якщо

Z > A ;

G =

A3 − B3

, якщо

Z < A ;

e(A + B)

, якщо

Z = A ;

P =lnA + B C ;

Q = A3 + p c ;

T =

Q ;

Q <7,5 ;

, якщо

x =

P + Q2

, якщо

Q > 7,5 ;

eT − p2

якщо

Q =7,5 ;

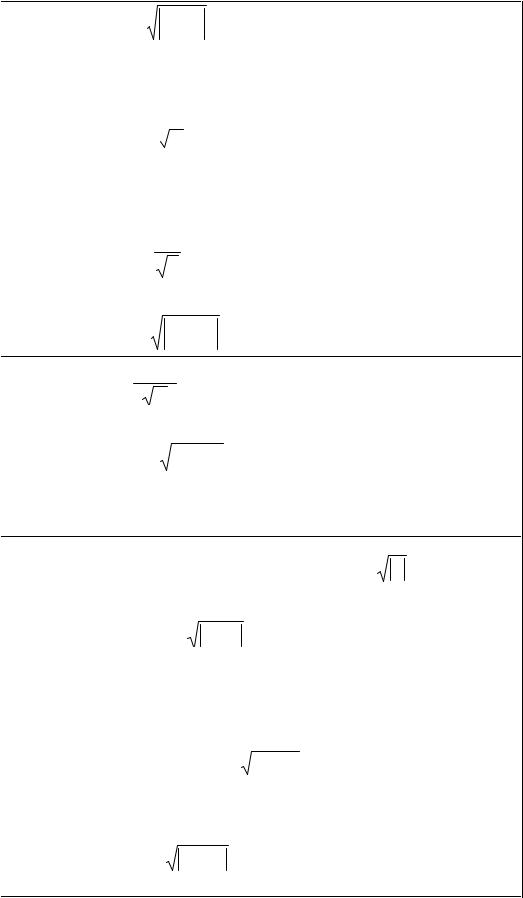
A = x - c2

; B =eA+1 ; D =(A + B)3 ;

x - B

, якщо

D >125 ;

y =

eA x

, якщо

D <125 ;

3 B sin x

якщо

D =125 ;

y =

x3 + ec

x = A + B2c ;

A B ; Z =ln (x + y2 ) ;

, якщо

y < Z ;

Q =

8,3 +sin(B + C)

, якщо

y > Z ;

3 x2 − Z

, якщо

y = Z ;

y =

x + B

B ; Z =

; G =ln (Z2 + y2 ) ;

B - x

ex - B2

, якщо

G +5 <10 ;

Q =

y2 + Z

, якщо G +5 >10 ;

G2 − y3

, якщо

G +5 =10 ;

y =

2 A

Z =

Q = y3 +

3 Z

5 C

;

sinA C ;

;

ey −c2

, якщо

y <9,5 ;

G =

Z - Q

, якщо

y =9,5

;

4 + ln2Q

, якщо

y >9,5

;

A =

tg x

Z =

eB+3

; B = A C3 ;

D C

D - C ;

sin x + B

, якщо

3 Z >7,5 ;

x =

ln2 (Z + D)

, якщо

3 Z <7,5 ;

Z5 −3

A − B

, якщо

3 Z =7,5 ;

10.

B −C

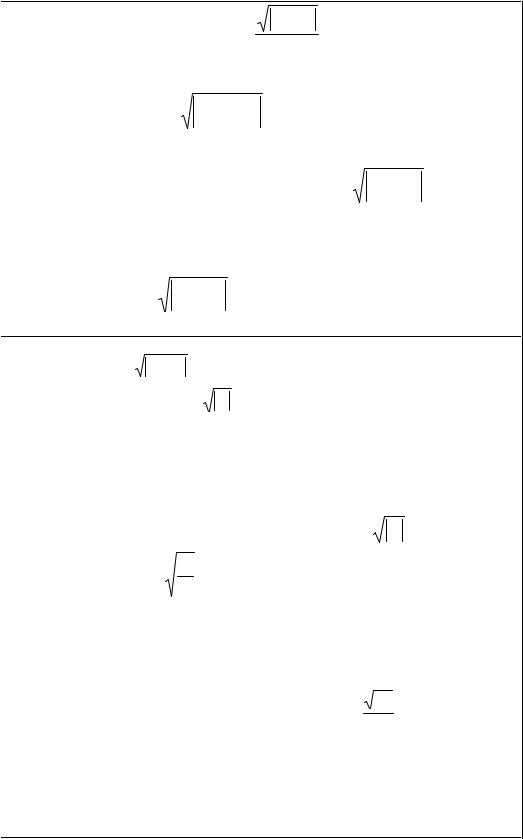
x =ln A2 + B ;

3 x

F =sin2B ;

;

F ex +1

, якщо

B >C ;

Q =

A2 − B2

B =C ;

, якщо

e3 p

, якщо

B <C ;

11.

y = B

x +1

Z =sin

(B + A

C = A2 − y

;

y > Z ;

;

ln B + A

, якщо

R =

tg B2

, якщо

y = Z

;

y + A3

, якшо

y < Z ;

B =

12.

Z = 4

C −D ; A = 3/x 2 - sin 2 D ;

C / 2D ;

x3 - 5 A

, якщо

Z > A ;

G =

3A3 −2B3

, якщо

Z < A ;

e2(A + B)/ 3

, якщо Z = A ;

P = lnA +

C ;

Q = A3 + p c

;

T = Q

;

13.

Q <7,5 ;

, якщо

x =

P + Q2

, якщо

Q >7,5 ;

eT − p2

, якщо

Q =7,5 ;

(x / 2); P = x2 −3F ;

T =

3 x 2

14.

F = tg

;

(d +1)/ ex

, якщо

> T ;

W =

P T

, якщо

P2 < T ;

sin x2

, якщо

= T ;

15.

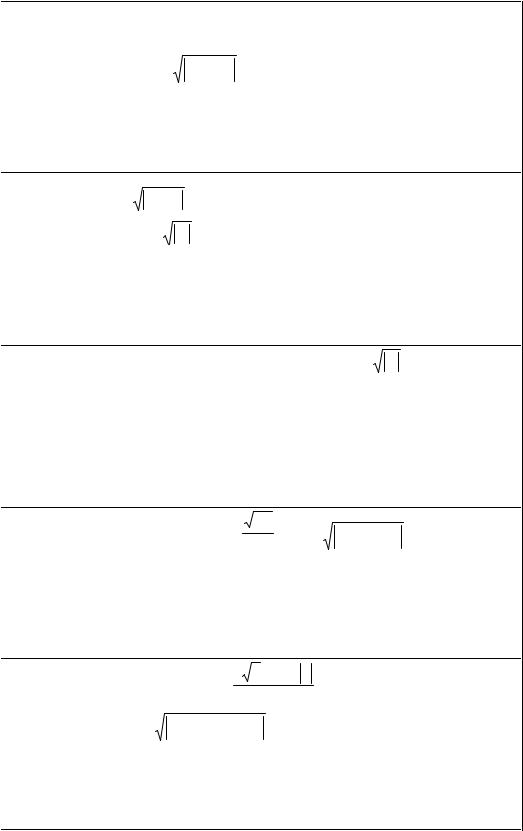
K = ln(a −b)+ 2c ;

N =

a 2 +

a ;

4 c

; Q = K / cos

3 a 2

+ b2

, якщо K < 0 ;

M =

e2N

, якщо K = 0 ;

sin b2

, якщо

K > 0 ;

16.

Z = 4 C + L ;

N = 3a - cos2 L ;

B =

C3 L2/3

;

a -

, якщо

;

D =

1/2N3 −2 / 3B3

, якщо Z > N ;

e(N + B)

, якщо

Z = N ;

G = lnA −B3 / T ; Y = A3 +G T ; T =

;

17.

B −3A1/2

, якщо

Y > 4 ;

S =

G3 / Y2

, якщо

Y < 4 ;

eT −G2

якщо Y = 4 ;

Z =cos3 (x) ;

Q =

T = 3 2x3 −8Z2

18.

5 / Z

;

(a -1)/ ex

, якщо

< T ;

L =

Q / T

, якщо

Q2 > T ;

tg x2

, якщо

Q2 =T ;

N =

x 2 −2 y

19.

M = sin(x − y)/ c ;

; Q = M +cos2 x/4 ;

3 cos x 2 +sin y2

, якщо

x = 0 ;

F =

e2N / c

, якщо x < 0 ;

tg y2

, якщо

x >0 ;

		A =	1	2
20.	Z = 6C −2sin D ;			cos	D ; B = 3 A +C / 3D ;
			2

x -

, якщо

Z < A ;

G =

- 4B

, якщо

Z = A

;

e(A + B)

, якщо

Z > A ;

P = 8B/C +sinA ; Q = A3 +

p/c ; T =

21.

;

3 A

Q = 3/ 4 ;

, якщо

x =

p −3Q2

, якщо

Q < 3/ 4 ;

eT − p2

, якщо

> 3 / 4

;

Z =

22.

= x / Z ; T =

; Q

+ Z

;

(b +1/ 2) ex , якщо

= T

;

K =

Q T

, якщо

> T ;

tg x2

, якщо

< T ;

M = cos(x − y)

N =

x 2 +3y

23.

−c

Q = M +ln(sin

;

x2 − y2

, якщо

Q > 0 ;

U =

e2N

, якщо

Q < 0 ;

tg y2

, якщо

Q =

;

I = 4 2C −3D ;

B = ln A +

24.

A =ln x - cos2D ;

lnx +3

якщо

I = A

;

A3 +cos B3

O =

, якщо

I > A

;

e(A + B)

, якщо

I < A

;

25.

P =

B −C ; Q = A3 −tgp +c ; T =

;

Q <7,5 ;

, якщо

x =

P + Q2

, якщо

Q > 7,5 ;

eT − p2

якщо

Q =7,5 ;

B3 −C3

26.

x =cosA2 −B ;

3 + 2x

;

F = ln(tg2 B) ;

F ex +1

, якщо

B >C ;

Q =

A2 − B2

, якщо

B =C ;

e3 p

, якщо B <C ;

27.

M = ln(sinx +cos y)+tgc ; N =

ctgx2

−

; Q = M / sinx ;

4 / sin c

x2 − y2

, якщо

x <0 ;

R =

e2N

, якщо

x =0 ;

tg y2

, якщо

x >0 ;

B =

cosA

28.

A = 4lnx - tg

Z = ln C −cos D ;

ln(sinC / cos D) ;

;

x -

якщо

Z > A ;

G =

A3 − B3

, якщо

Z < A ;

e(A + B)

, якщо

Z = A ;

T = lnA +tgB C

;

W = A3 +ctg3T 8c

;

J =

;

29.

, якщо

W = 8 ;

V =

9J +Q2

, якщо

W > 8 ;

eT −T2

якщо W < 8 ;

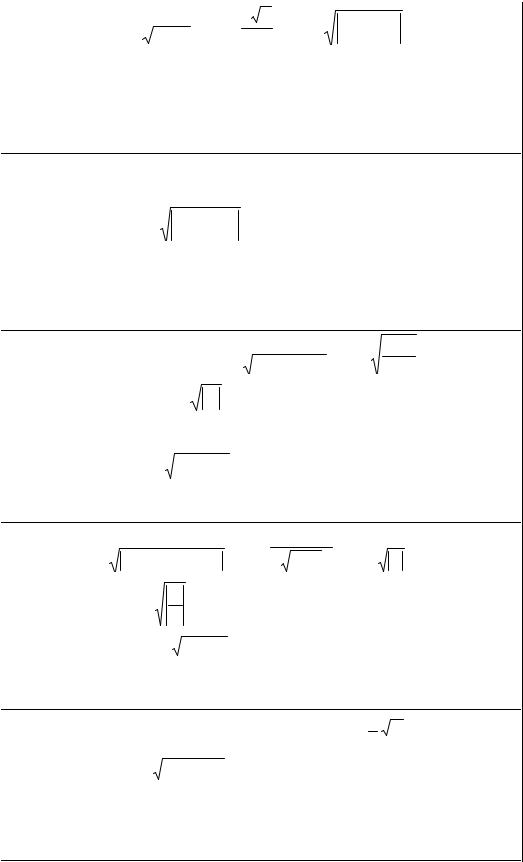
30.

Z = x

Q =

2 x

;

T =3

x2 + Z2

;

5 / Z

(a -1) ex

, якщо

> 3

;

S =

Q T

, якщо

< 3 ;

tg x2

, якщо

= 3

;

M = 5x +9y −

N =

x 2 −siny

31.

Q = M(3 +sin

x) ;

;

tgc

(x 2

− y2 )5

, якщо

N < 8 ;

R =

e2N +4

, якщо

N = 8 ;

tg y2

, якщо

N > 8 ;

Z = 20C +

D ; A =

B = 3

32.

4x - cos2 D ;

C D

;

x -

, якщо

Z > A ;

G =

A3 −B3

, якщо

Z < A ;

e(A + B)

, якщо

Z = A ;

Q =

A3 + P c

33.

P = tgA +sin(B C)

tgP3

T =

Q +6

;

, якщо

Q <T ;

x =

P + Q 2

, якщо

Q >T ;

sin 2 (eT −p2 )

якщо

Q =T ;

T = tgx + 65

34.

Z = x +7 ;

Q = Z −2ln x ;

;

(a -1) ex

, якщо

Q2 >T ;

S =

3 +7ln

Q T

, якщо Q2 <T ;

tg x2

, якщо

Q2 =T ;

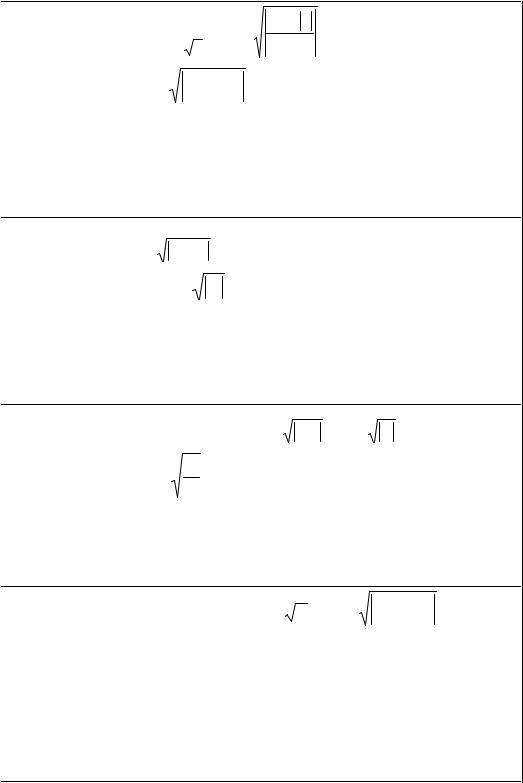
35.

N =

x 2 − y

M = ctg(x + y)+

4 c

c ;

;

Q = (M sin x)

x2 − y2

Q <

;

, якщо

e2N

Q =

R =

, якщо

2 ;

tg y2

Q >

, якщо

2 ;

A = 4x +

B =

36.

Z = sin ex + 44 C + D

- cos

D ;

C D

;

x -

якщо

Z > 3A ;

I =

A3 − B3

, якщо

Z < 3A

;

e(A + B)

, якщо

Z = 3A ;

37.

P = 2lnA +

B C ; Q = A3 +

p c ; T =

Q +12 ;

Q < e2 ;

, якщо

R =

P + Q2

, якщо

Q > e2 ;

eT − p2

, якщо

Q = e2 ;

F =8 sin

(x π) ; c =lnA +

G =3

C2 − F2 ,

38.

AC2

, якщо

C2 <9

C2 >9

y =

e c

, якщо

lnF

C2 =9

G C , якщо

;

39.	P =sin2 (x π) + A2 ; F =	3 x	; Q =(P F)3 ;
		4 A

ln (F2 + Q) ,

якщо

Q > 27

R =

eP X

якщо

Q < 27

Q - P2

якщо

Q = 27

Z = ln2 C2 +1; A =

; B = Z3 A ;

40.

B sinAx

c x

A < B

, якщо

S =

ex 2

, якщо

A > B

Z2 − A2

, якщо

A = B

A x

41.

A = x2

B =sin2 y2

C =

;

4 B ;

x3 + lnA2

якщо

C2 > 25

D =

C2 − B

, якщо

< 25

epx

якщо

C2 = 25

42.

A2 - B2

R = A x

; P = A3 −B sin2x ; H = ln(R + P2)

tg2 Bx

, якщо

H > 5

y =

3 p2 + H2

, якщо

H < 5

ex+A

якщо

H = 5

43.

(P +1)2

Z = sin2 (A - B) ; P

; Q =

(Q − A)/(Q + A)

, якщо

Q > 3

I =

tg(Q + P)

якщо

Q < 3

Z 2

Q = 3

, якщо

44.

x =

A3 - B3

;

y = 9,2

x +3

; Z = x -

+ y ;

Z2 > 25

A Z

, якщо

R =

cos2 y + B2

, якщо

Z2 < 25

y - Z

, якщо

= 25

45.

= sin2 (A + B) ;

C =

A + B ; E = 23 D

A C2

C3 - eD

, якщо

3E >100

Z =

tgC E

, якщо

3E <100

3 A E

, якщо

3E =100

46.

y =

B3 +C ; x = ey+B ; Z = tgx2

x +c

Z >

, якщо

cos2 (y + x)

Z <

H =

, якщо

3 17 + y

Z =

, якщо

47.

V =

sin2x

AB ; y = ln(A + B)2 ; Z = y2 - 5

V + A3

, якщо

y < V2

P =

3 Z2 + x2

, якщо

y > V2

= sin 2A +

Z = tg

2 A

; T = e

- 3 Z

48.

BC ;

4A2B +C

, якщо

Z >15

x =

y + A3

, якщо

Z <15

ln(y +T)2

якщо

Z =15

49.

P = A

sinx2 ;

R =

x 2 +3

; Q = P3 - R

A P

tg2 x -

Q > A

, якщо

Z =

R 2 −

, якщо

Q < A

lnP - eA

якщо

Q = A

50.	A =	x + y		3	x	2
		x y ;	B =				; C = sin2B ;
					A
		35 + A C	,	якщо			B2 > 81
	D =	ln2A - C		,	якщо B2 < 81
	eB+C		,	якщо			B2 = 81

<<< < Предыдущая 12 / 112 3 4 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.03.2025309.25 Кб0MU_KR_ISI_2012_ukr (2).doc
#
15.08.20191.03 Mб8Mu_K_Lab_Rab_Pp2011.doc
#
19.09.2019130.56 Кб1mu_praktika_2011.doc
#
10.02.2016351.23 Кб13MU_VIROBNIChA_PRAKTIKA_OA_2011_dlya_studentov.doc
#
01.07.20251.03 Mб0MV1306_ua.doc
#
10.02.2016529.51 Кб10MV1339.pdf
#
10.02.2016764.47 Кб20MV1962-Лабы.pdf
#
10.02.2016723.45 Кб4MV1971-1.pdf
#
16.09.2019467.46 Кб3MV2800Avtomobilnyy_transpor.doc
#
10.02.2016298.08 Кб3MV3012.pdf
#
10.02.2016551.56 Кб4MV3047.pdf