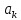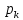teoria_veroyatnosti
.docx
Министерство Образования и Науки Украины
Одесский Национальный Политехнический Университет
Институт Бизнеса, Экономики и Информационных Технологий
Кафедра экономической кибернетики и информационных технологий
Расчетно-графическая работа
По дисциплине: «Теории вероятностей и математическая статистика»
Вариант - 12
Выполнила:
Студентка гр. ОИ-121
Ушкова А.Ю
Проверили:
Андриенко В. М.
Журавлёва Н. М.
Одесса
2013
Завдання №1
Виробляються послідовні незалежні випробування 3 приладів на надійність. Кожний наступний прилад випробовується тільки в тому випадку, якщо попередній виявився надійним. Імовірність витримати випробування для кожного приладу дорівнює 0,93.
Знайти:
-
ряд розподілу випадкового числа випробуваних приладів;
-
функцію розподілу й побудувати її графік;
-
математичне очікування й дисперсію.
Розв’язання
1. Розв’яжемо задачу при N=3, p=0,93.
а)
Дискретна випадкова
величина
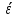 - число випробуваних приладів. Можливі
значення цієї випадкової величини:
- число випробуваних приладів. Можливі
значення цієї випадкової величини:
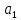 = 1,
= 1,
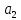 = 2,
= 2,
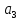 =3.
Знайдемо ймовірності цих значень.
Позначимо події:
=3.
Знайдемо ймовірності цих значень.
Позначимо події:
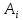 - і-ий випробуваний прилад виявився
надійним,
- і-ий випробуваний прилад виявився
надійним,
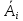 - і –ий випробуваний прилад виявився
надійним. Тоді
- і –ий випробуваний прилад виявився
надійним. Тоді
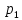 =
Р(
=
Р(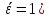 =
Р(
=
Р(
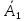 )=
1-0,93=0,07
)=
1-0,93=0,07
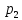 =
Р(
=
Р(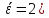 =
Р(
=
Р(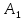
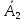 )=0,93*0,07=0,0651
)=0,93*0,07=0,0651
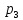 =
Р(
=
Р(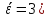 =Р(
=Р(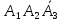 +
+
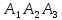 )
= 0,93*0,93*0,07+0,93*0,93*0,93=0,864
)
= 0,93*0,93*0,07+0,93*0,93*0,93=0,864
|
|
1 |
2 |
3 |
|
|
0.07 |
0.0651 |
0.8649 |
б)
Функцією розподілу F(x),
яка визначена для будь-якого дійсного
х,називається
ймовірність того, що випадкова величина
Ƹ прийме значення менше х,
тобто
F(x)=P(Ƹ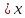 ),
де -
),
де - .
Оскільки функція F(x)
визначена для всіх дійсних значень х,
то розглянемо послідовно інтеграли:
.
Оскільки функція F(x)
визначена для всіх дійсних значень х,
то розглянемо послідовно інтеграли:
1)
х
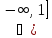 ,
F(x)
= Р (Ƹ
,
F(x)
= Р (Ƹ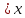 )
=0, тому що подія (Ƹ
)
=0, тому що подія (Ƹ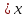 )
для такого х
є
неможливою подією.
)
для такого х
є
неможливою подією.
2)
х
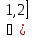 ,
F(x)
= Р(Ƹ=1)=0,07, тут нерівності Ƹ
,
F(x)
= Р(Ƹ=1)=0,07, тут нерівності Ƹ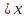 задовольняє єдине значення Ƹ=1
і
Ƹ=2
задовольняє єдине значення Ƹ=1
і
Ƹ=2
3)
х
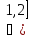 ,
F(x)
= Р(Ƹ=1) + Р(Ƹ=2)= 0,07+0,0651=0,1351
,
F(x)
= Р(Ƹ=1) + Р(Ƹ=2)= 0,07+0,0651=0,1351
4)
х
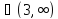 ,
F(x)
= Р(Ƹ=1) + Р(Ƹ=2)+ Р(Ƹ=3)=0,07+0,0651+0,8649
,
F(x)
= Р(Ƹ=1) + Р(Ƹ=2)+ Р(Ƹ=3)=0,07+0,0651+0,8649 1,
тут нерівності Ƹ
1,
тут нерівності Ƹ
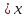 задовольняють всі значення Ƹ.
Таким чином,
задовольняють всі значення Ƹ.
Таким чином,
F(x)=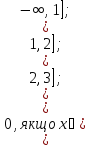
Графік функції розподілу наведен на Рисунку 1.
 F(x)
F(x)






 1
1









 0,135
0,135







 0,07
0,07



1 2 3 x
Рисунок 1. Графік розподілу випадкової величини Задачи 1.
в) Знайдемо математичне сподівання та дисперсію.
n
М(Ƹ)=
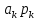 =1*0,07
+ 2*0,065 + 3*0,8649=2,7319,
=1*0,07
+ 2*0,065 + 3*0,8649=2,7319,
k=1
n
D(Ƹ)=M(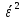 )–(M(
)–(M(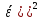 =
=
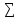
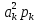 -
-
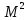 (Ƹ)
= 1*0,07+4*0,0651+9*0,8649–(2,7319
(Ƹ)
= 1*0,07+4*0,0651+9*0,8649–(2,7319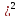 =
=
k=1
=0,07+0,2604+7,7841-7,4632=0,41694.
Завдання №2
Параметр
а знайдемо із властивості
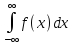 =1,
інтеграл
=1,
інтеграл
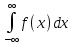 розіб’ємо
на суму трьох інтегралів
розіб’ємо
на суму трьох інтегралів
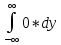 +
+
 +
+
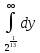 =
=
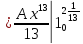 =
=
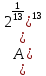 =
=
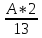 = 1
= 1
A=
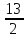 =6,5
=6,5
f(x)=
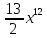
Намалюємо графік розподілу f(x) (Рисунок 2)

F(x)
1


0,65





0 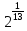 x
x
Рисунок 2. Графік щільності розподілу f(x)
Обчислимо
функцію розподілу, для цього розглянемо
інтервали (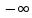 ,0),
[0,
,0),
[0,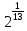 ],
(
],
(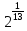 ,+
,+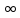 )
)
-
х
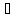 (
(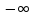 ,0),
F(x)=
,0),
F(x)=
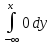 =0
,
=0
,
-
х
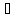 [0,
[0,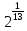 ],
F(x)=
],
F(x)=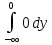 +
+
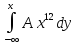 =
=
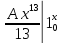 =
=
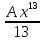 =
=
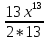 =
=
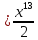
-
х
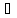 (
(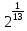 ,+
,+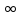 ),
F(x)=
),
F(x)=
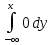 +
+
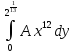 +
+
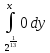 =
=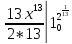 =
=
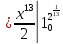 =
=
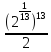 =1
=1
Графік функції наведений на Рисунку 3.
Обчислимо математичне сподівання й дисперсію:
M(Ƹ)=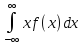 =
=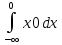 +
+
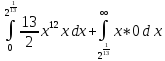 =
=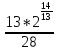 =
=
=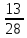 *
*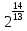
D(Ƹ)=M(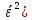 -
-
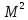 (Ƹ)=
(Ƹ)=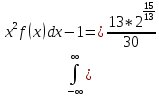 – 1 =
– 1 =
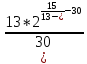
 F(x)
F(x)

 1
1

0
 x
x
Рисунок 3. График розподілу неперервної випадкової величини
(1,2)
р(1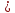 Ƹ
Ƹ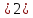 =
=
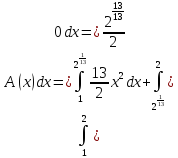 + 0 = 1.
+ 0 = 1.