
1.6 Решение слау по формулам Крамера
Пусть имеется система (6):
 ,
,
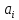 ,
, ,
, и
и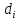 (i
(i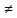
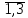 )
- заданные числа, х,y,
z
– неизвестные.
)
- заданные числа, х,y,
z
– неизвестные.
Определитель
 этой системы равен:
этой системы равен:
 =
=
 .
.
Если элементы первого
столбца этого определителя заменить
на числа
 , то получим определитель
, то получим определитель
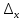 =
=
 .
.
При замене второго
столбца определителя
 числами
числами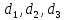 получим определитель
получим определитель
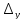 =
=
 .
.
Аналогично получаем
определитель
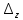 =
=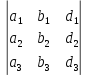 .
.
x=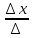
y
=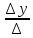
z=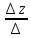
Если
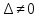 , то система (6) имеет единственное
решение, которое определяется по
формулам Крамера:
, то система (6) имеет единственное
решение, которое определяется по
формулам Крамера:
(10)
Если
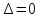 и хотя бы один из определителей,
и хотя бы один из определителей,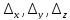 не равен нулю, то система несовместна.
не равен нулю, то система несовместна.Если
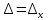 =
=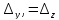 = 0 , то система несовместна или имеет
бесконечно много решений.
= 0 , то система несовместна или имеет
бесконечно много решений.
Пример 22: Решить систему уравнений , используя формулы Крамера (10).
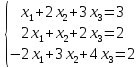
Решение: Определитель системы равен
 =
=
 = 4+18-8+6-6-16 = -2
= 4+18-8+6-6-16 = -2
Вычислим вспомогательные определители:
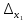 =
=
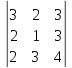 = 12+18+8-6-18-16 = -2
= 12+18+8-6-18-16 = -2
 =
=
 = 2 · 2 ∙
= 2 · 2 ∙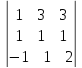 = 4 · (2+3-3+3-1-6) = -8
= 4 · (2+3-3+3-1-6) = -8
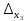 =
=
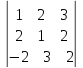 = 2+18-8+6-6-8 = 4
= 2+18-8+6-6-8 = 4


 Решение
системы:
Решение
системы:
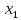 =
=
 =
=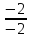 = 1
= 1
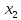 =
=
 = 4
= 4
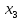 =
=
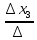 =
=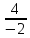 = -2
= -2
Ответ:
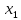 =1 ,
=1 ,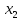 = 4 ,
= 4 ,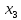 = -2 .
= -2 .
1.7 Решение слау матричным методом
( (Е
· Х = Х)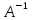 ·
А = Е)
·
А = Е)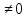 .
Умножив обе части матричного уравнения
(8)A · X = B
слева
на матрицу
.
Умножив обе части матричного уравнения
(8)A · X = B
слева
на матрицу
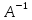 , получим :
, получим :
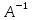 · А · Х =
· А · Х =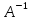 · В
· В
Е · Х =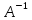 ·B
·B
Х = · В - решение матричного уравнения.
(11)
· В - решение матричного уравнения.
(11)
Пример 23 Решить систему уравнений матричным методом.
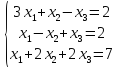
Решение: А=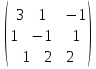 – матрица системы, В =
– матрица системы, В = – столбец свободных членов, Х =
– столбец свободных членов, Х =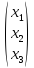 – столбец неизвестных.
det A =
– столбец неизвестных.
det A =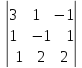 = -6-2+1-1-6-2 = -16
= -6-2+1-1-6-2 = -16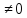 =
= Ǝ
Ǝ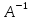 ; ( символƎ
- от “exist”
- существует)
; ( символƎ
- от “exist”
- существует)
Найдем все алгебраические дополнения матрицы А:
|
|
|
|
 = -
= -
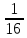
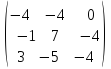
Получим решение системы, используя формулу (11):
Х =
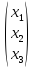 = -
= -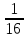
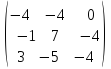 ·
·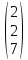 = -
= -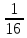
 = -
= -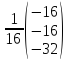 =
=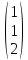
Ответ:
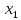 =1 ,
=1 ,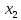 = 1 ,
= 1 ,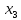 = 2 .
= 2 .
1.8 Решение слау методом Гаусса
Рассмотрим систему (7)
Матрица (9) системы, к которой присоединен столбец свободных членов B, называется расширенной матрицей системы:
à =

Элементарными преобразованиями в расширенной матрице называются преобразования, которые не меняют множество решений системы.
Для обозначения элементарных преобразований используют знак ∼.
Элементарными преобразованиями в расширенной матрице являются:
перемена местами строк;
перемена местами столбцов с запоминанием, какому неизвестному соответствует каждый столбец;
умножение (деление) строки на число, отличное от нуля;
прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и то же число;
вычеркивание одной из двух пропорциональных (равных) строк;
вычеркивание нулевой строки.
Метод Гаусса – один из наиболее универсальных и эффективных методов решений СЛАУ, состоит в последовательном исключении неизвестных. На первом этапе решения (прямой ход) расширенная матрица системы с помощью элементарных преобразований приводится к так называемому ступенчатому (в частности, треугольному) виду. На втором этапе (обратный ход) идет последовательное определение неизвестных из полученной эквивалентной системы.
Опишем метод Гаусса подробнее на примере системы трех уравнений.
Пример 24. Решить систему уравнений
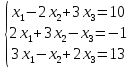
Решение: Прямой ход: применяем к расширенной матрице системы Ã элементарные преобразования так, чтобы ниже главной диагонали стояли только нули.


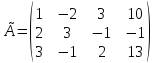
1-ый шаг – формирование первого столбца:
Первую строку сохраняем, ко второй строке прибавим первую, умноженную на (-2), к третей прибавим первую, умноженную на (-3). После этого в первом столбце получаем два нуля.


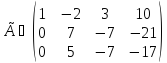
2-ой шаг – формирование второго столбца:
Первую строку сохраняем, вторую делим на 7.


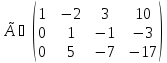
К третьей строке прибавим вторую, умноженную на (-5). После этого имеем все нули ниже главной диагонали.


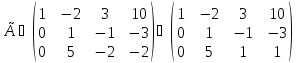
Третью строку разделим на (-2).
Система, эквивалентная данной с полученной расширенной матрицей имеет треугольный вид:
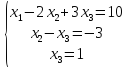
Обратный ход: из последнего
уравнения
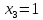 ,
,
из второго:
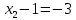 ,
получаем
,
получаем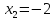 ,
,
из первого:
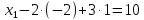 ,
получаем
,
получаем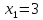 .
.
Ответ:
 ,
,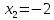 ,
,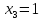 .
.
Замечание 10. Совместная система уравнений будет определенной, если в процессе преобразований она приводится к треугольному виду: число неизвестных системы равно числу уравнений. И неопределенной, если приводится к ступенчатому виду: число неизвестных системы больше числа уравнений.
Уравнение
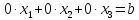 ,
гдеb≠0
не имеет решений. Оно называется
противоречивым. Система, содержащая
такое уравнение, сама противоречива,
т.е. несовместна.
,
гдеb≠0
не имеет решений. Оно называется
противоречивым. Система, содержащая
такое уравнение, сама противоречива,
т.е. несовместна.
Замечание 11. На практике
удобно, чтобы коэффициент
 (уравнения
переставить местами, либо разделить
обе части уравнения на
(уравнения
переставить местами, либо разделить
обе части уравнения на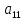 ).
).

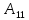 =
-4
=
-4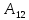 =
-1
=
-1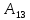 =
3
=
3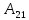 = -4
= -4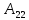 = 7
= 7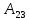 = -5
= -5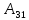 =
0
=
0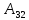 =
-4
=
-4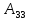 = -4
= -4