
Справочный материал
Раздел I. Линейная алгебра
1.1 Матрицы Прямоугольная таблица чисел, состоящая из m строк и n столбцов называется числовой матрицей порядка (размера) mxn:
A =
 (1)
(1)
Сокращенно: А= (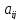 ),
),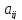 –
элементы матрицы,i
– номер строки, j
– номер столбца,
–
элементы матрицы,i
– номер строки, j
– номер столбца,
i = 1,2,…,m (i=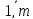 ),
j = 1,2,…,n (j=
),
j = 1,2,…,n (j=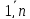 ).
).
Виды матриц :
Если m=n , то матрицу называют квадратной ;
Если m=1 – матрицей-строкой ;
Если n=1 – матрицей-столбцом.
В частности,
A
=
 -
квадратная матрица 2-ого порядка.(2)
-
квадратная матрица 2-ого порядка.(2)
A
=
 -
квадратная матрица 3-его порядка,(3)
-
квадратная матрица 3-его порядка,(3)
Числа a11, a22, a33 образуют главную диагональ ( i=j )
Ряд определений в дальнейшем будет дан для матрицы (3).
 –матрица-строка порядка
1х3,
–матрица-строка порядка
1х3,
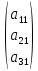 –матрица-столбец порядка
3х1 .
–матрица-столбец порядка
3х1 .
Квадратная матрица, имеющая ненулевые элементы только на главной диагонали, называется диагональной:
diag A =

Диагональная матрица, все элементы главной диагонали которой равны единице, называется единичной:
E
=

Сокращенно : E= (δij)
δij
=
 - символ
Кронекера.
- символ
Кронекера.
Прямоугольная (в общем случае) матрица, все элементы которой равны нулю, называется нулевой:
0
=
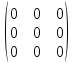
Замена каждой строки матрицы A её соответствующим столбцом называется транспонированием. Транспонированная по отношению к матрице A матрица обозначается
 :
:
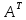 =
=
 ,
,
очевидно,
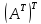 =A
=A
Пример 1 Классифицировать следующие матрицы:
A
=
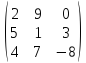 ,B
=
,B
=
 ,D
=
,D
=
 ,
,
С =
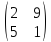 ,G
=
,G
=
 ,F
=
,F
=
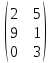 ,
,
N
=
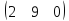 ,Q
=
,Q
=
 ,K
=
,K
=
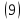 .
.
Решение: A, B, D, C – квадратные матрицы,
A, B, D – 3-его порядка, C – 2-ого.
G, F – прямоугольные, соответственно 2х3 (содержащая две строки и три столбца)
и 3х2 (три строки и два
столбца) – порядка, N
– матрица-строка
1х3 порядка, Q
– матрица-столбец
3х1 – порядка, K
– матрица-скаляр
(число), D
– диагональная,
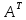 =B
,
=B
,
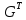 =F
,
=F
,
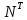 =Q
.
=Q
.
1.2 Действия над матрицами
Матрицы А и В одной размерности считаются равными, если равны их соответствующие элементы: А=В
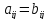
Сложение(вычитание) матриц одинакового размера осуществляется поэлементно:
С = А + В , если
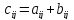
Умножение матрицы на число λ – каждый элемент матрицы умножается на это число:
B = λ
× A
,
если
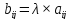
2) и 3) - линейные операции над матрицами.
Замечание 1: Сложение (вычитание) и умножение матрицы на число – линейные операции над матрицами.
Пример 2 Найти сумму матриц A + B из Примера 1
Решение: А + В =
 =
=
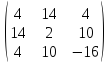
Замечание 2: Матрица А + В симметричная, справедливо равенство:
А
+ В =
 .
У симметричной матрицы элементы,
симметричные главной диагонали равны.
.
У симметричной матрицы элементы,
симметричные главной диагонали равны.
Пример 3
Найти линейную комбинацию матриц 2А +
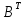 - 4Е ,
если
- 4Е ,
если
А =
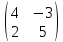 , В =
, В = , Е =
, Е =
Решение:
2 ∙ А =
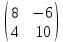 ,
, =
=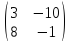 , 4Е =
, 4Е =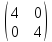 .
.
2А +
 - 4Е =
- 4Е =
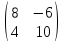 +
+
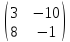 -
-
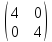 =
=
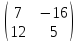
Умножение матриц.
Произведение А
∙ В определяется
не для произвольных матриц А
и В. Оно
имеет смысл только в том случае,
когда число столбцов матрицы А
ровно числу строк
В. При
этом А ∙ В есть
матрица С ,
каждый элемент
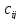 которой
равен сумме последовательных произведений
элементов i-
той строки матрицы А
на соответствующие
элементы j-
того столбца
матрицы В.
которой
равен сумме последовательных произведений
элементов i-
той строки матрицы А
на соответствующие
элементы j-
того столбца
матрицы В.
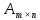 ∙
∙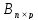 =
=
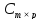
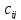 =
=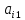 ∙
∙
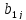 +
+
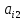 ∙
∙
 + … +
+ … +
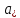 ∙
∙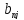 =
=
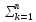
 ∙
∙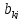 , i
=
, i
=
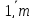 , j=
, j=
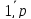 .
.
Найти произведения матриц:
Пример 4
 ∙
∙ =
=
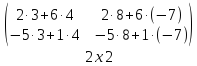 =
=
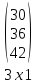
Пример 5
 ∙
∙ =
=
 =
=
Пример 6
А ∙ В
=
 ∙
∙ =
=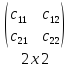
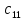 = 4 ∙ (-2) + 1 ∙ 3 + 5 ∙ 0 = -5
= 4 ∙ (-2) + 1 ∙ 3 + 5 ∙ 0 = -5
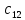 = 4 ∙ 6 + 1 ∙ 7 + 5 ∙ (-1) = 26
= 4 ∙ 6 + 1 ∙ 7 + 5 ∙ (-1) = 26
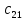 = 3 ∙ (-2) + 0 ∙ 3 + 2 ∙ 0 = -6
= 3 ∙ (-2) + 0 ∙ 3 + 2 ∙ 0 = -6
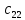 = 3 ∙ 6 + 0 ∙ 7 + 2 ∙ (-1) = 16
= 3 ∙ 6 + 0 ∙ 7 + 2 ∙ (-1) = 16
А ∙ В =

На рисунке
1 схематично
показано получение элемента
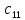 в произведении матриц :
в произведении матриц :
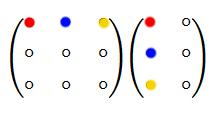
Рисунок 1
Рисунок 2
получение элемента
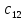 :
:
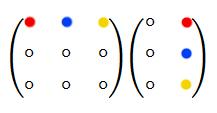
Рисунок 2
Пример 7
B
∙ A
=
 =
=

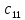 = -2 ∙ 4 + 6 ∙ 3 = 10 ;
= -2 ∙ 4 + 6 ∙ 3 = 10 ; 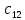 = -2 ∙ 1 + 6 ∙ 0 = -2 ;
= -2 ∙ 1 + 6 ∙ 0 = -2 ;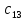 = -2 ∙ 5 + 6 ∙ 2 = 2 ;
= -2 ∙ 5 + 6 ∙ 2 = 2 ;
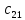 = 3 ∙ 4 + 7 ∙ 3 = 33 ;
= 3 ∙ 4 + 7 ∙ 3 = 33 ; 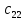 = 3 ∙ 1 + 7 ∙ 0 = 3 ;
= 3 ∙ 1 + 7 ∙ 0 = 3 ; = 3 ∙ 5 + 7 ∙ 2 = 29 ;
= 3 ∙ 5 + 7 ∙ 2 = 29 ;
 = 0 ∙ 4 + (-1) ∙ 3 = -3 ;
= 0 ∙ 4 + (-1) ∙ 3 = -3 ; 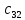 = 0 ∙ 1 + (-1) ∙ 0 = 0 ;
= 0 ∙ 1 + (-1) ∙ 0 = 0 ;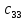 = 0 ∙ 5 + (-1) ∙ 2 = -2.
= 0 ∙ 5 + (-1) ∙ 2 = -2.
Замечание 3: В общем случае АВ ≠ ВА (примеры 6-7).
Матрицы, для которых выполняется равенство АВ = ВА называются коммутативными.
Пример 8
А ∙ В =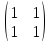 ∙
∙
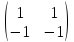 =
=

А ∙ В = 0 (Хотя А ≠ 0, В ≠ 0)
Замечание 4: В теории матриц нулевая матрица 0 и единичная Е играют роль чисел соответственно 0 и 1 в арифметике, т.е.
ЕА = АЕ = А , А ∙ 0 = 0 ∙ А = 0, А + 0 = 0 + А.
