П.2.4.Деление комплексных чисел

Деление определяется как действие, обратное умножению. Частным двух комплексных чисел z₁ и z₂≠0 называется комплексное число z, которое, будучи умноженным на z₂, дает число z₁, т. е. z₁/z₂=z, если z₂z=z_1.

Если положить z₁=x₁+iy₁; z₂=х₂+iy₂≠0, z=х+iy, то из равенства (х₂+iy₂)(x+iy)=x₁+iy₁ следует

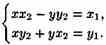
Решая систему, найдем значения х и у:

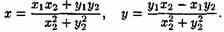
Таким образом,

На практике частное двух комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю («избавляются от мнимости в знаменателе»).

П.2.5.Извлечение корней из комплексных чисел Извлечение корня n-й степени определяется как действие, обратное возведению в натуральную степень.

Корнем n-й степени из комплексного числа z называется комплексное число ω, удовлетворяющее равенству ωⁿ=z, т. е., если ωⁿ= z.

Если положить z=r(cosφ+isinφ), а ω=r(cosθ+isinθ), то, по определению корня и формуле Муавра, получаем

z=ωⁿ =rⁿ(cos nθ+isin nθ)-r(cosφ+isinφ).

Отсюда имеем rⁿ=r, nθ=φ+2πk, k=0,-1,1,-2,2,... To есть

и    (арифметический корень).

Поэтому равенствопринимает вид

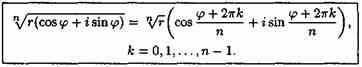
Получим n различных значений корня. При других значениях k, в силу периодичности косинуса и синуса, получатся значения корня, совпадающие с уже найденными. Так, при k=n имеем

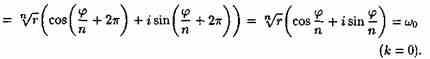
Итак, для любого z≠0 корень n-й степени из числа z имеет ровно n различных значений.

Примеры

Пример №1

Записать комплексные числа z₁=-1+i и z₂=-1в тригонометрической и показательной формах.

Решение: Для z₁ имеем

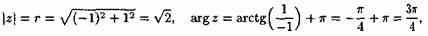
т. е. φ=3p/4.

Поэтому

Для z₂ имеем

т. е. j=p. Поэтому -1=cosπ+isinπ=е^iπ.

Пример №2

Найти  

Решение: Запишем сначала число  в тригонометрической форме:

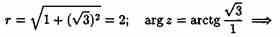
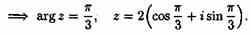
По формуле Муавра имеем

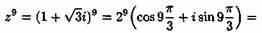
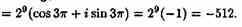
Пример №3

Выполнить деление   

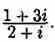
Решение:

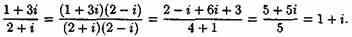
Для тригонометрической формы комплексного числа формула деления имеет вид

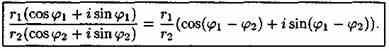
При делении комплексных чисел их модули, соответственно, делятся, а аргументы, соответственно, вычитаются.

Пример №4

Найти значения  

Решение: а) Запишем подкоренное выражение в тригонометрической форме:

.

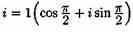Стало быть,

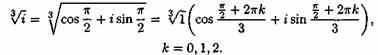
При k=0 имеем

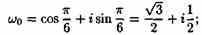
при k=1 имеем

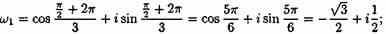
при k=2 имеем

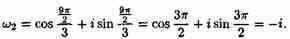
б) Снова запишем подкоренное выражение в тригонометрической форме:

-1=cosπ+isinπ.

Поэтому

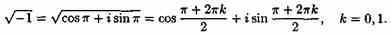
При k=0 получаем ω₀=cos/2+isin/2=i, а при k=1 получаем

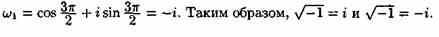
Пример №5

 Выполнить действия:

a)       b)

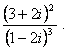
Решение. Выполняем действия как над многочленами

а)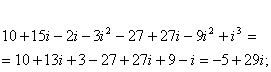

 

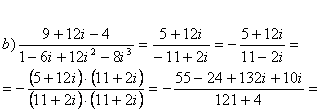
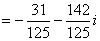
Пример №6

 

Построить на комплексной плоскости и представить в тригонометрической и показательной формах следующие комплексные числа:

1)  2)  3)  4)  5) .

Решение. Сначала построим все эти точки на комплексной плоскости

Теперь представим их в тригонометрической и показательной формах:

1)     

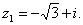
 Имеем: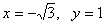 

 

 

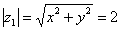
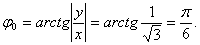
 Так как 2- ой четверти, то

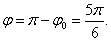
 Тригонометрическая форма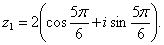  

Показательная форма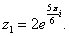 

 

2)     

 

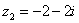
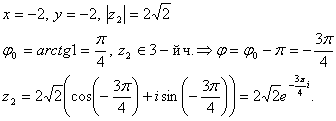
3)     

 

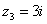
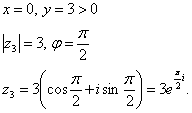
4)     

 

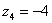
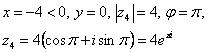
5)     

 

 

 

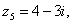
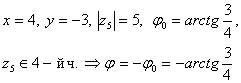
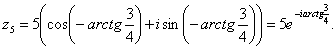
Пример №7

Представить в показательной форме числа:

1)       

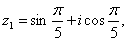
2) 

3) 

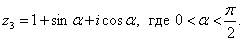
Решение.

1)     

 

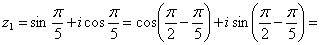
2)     

 

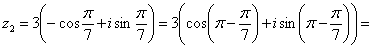
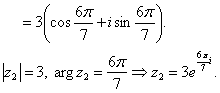
3)     

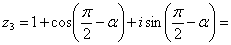
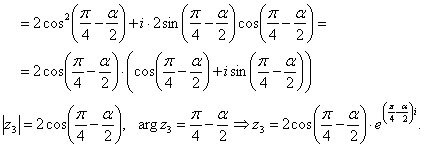
Пример №8

Выполнить действия:

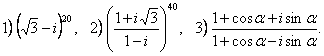
Решение.

1)      Представим число в тригонометрической форме

 

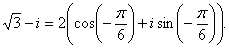
По формуле Муавра получим:

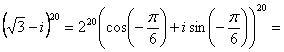
2)      Имеем: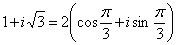 

 

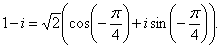
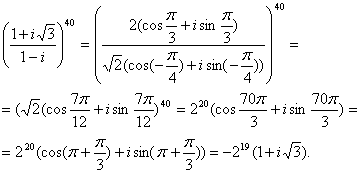
3)       

 

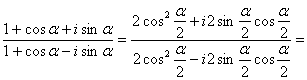
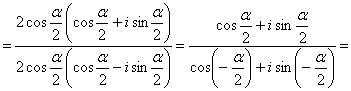
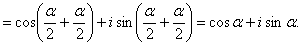
Пример №9

 Построить график функции .

Решение.

Эта функция вида , то есть четная функция и, следовательно, график ее симметричен относительно оси OY.

  Учитывая, что , то следует построить график функций сдвигом вдоль оси OX на 4 единицы графика функции .

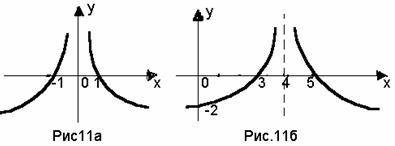
Итак:

1)      строим график функции 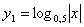 (рис.11а);

2)      сдвигом его на 4 единицы по оси OX строим график функции 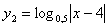  ( рис. 11б ); 

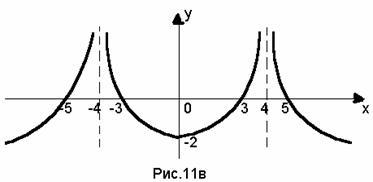
3)      сохраняем правую часть ( для  ) графика функции и ее отображаем симметрично относительно оси OY. Для уточнения графика определим точку пересечения графика с осью OY. При  , т.е. точка пересечения графика с осью OY: ( 0;-2 ). График функции  представлен на рис.11в.

 

 

Пример №10

Построить график функции .

Решение.

Так как ,то функция четная и график ее симметричен относительно оси OY. Значения x, при которых выражение, стоящее под знаком логарифма, обращается в нуль, являются недопустимыми для x и одновременно они помогают найти вертикальные асимптоты. Найдем их.

Имеем:

 

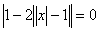
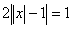
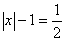  или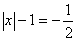 

  .

График имеет четыре вертикальные асимптоты

.

Определим нули функции. Имеем:

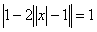
или 

  .

Итак, на оси OX имеется пять точек графика функции:

(-2;0), (-1;0), (0;0), (1;0), (2;0). График функции имеет четыре асимптоты. Для построения графика необходимо знать с какой стороны ветви графика приближаются к асимптотам. Для этого достаточно определить интервалы знакопостоянства функции. Напомним, что

.

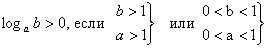
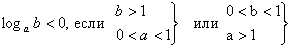Решим неравенство

 

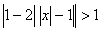
1) 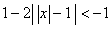  или 2)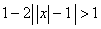 

 

или  Ǿ

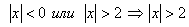
Итак, если , то y>0 и, следовательно, если   и , то . Поэтому график функции в интервале 

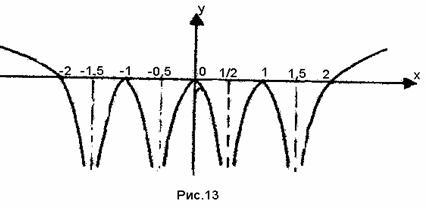  (-2;2) расположен ниже оси OX, а в интервалах (-∞;-2), (2;+∞) – выше оси OX ( рис.13 ).