Описание работы схемы

На рис.1 показана принципиальная схема позиционной электромеханической следящей системы. Согласно схемы, при идентичных положениях ползунков задающего потенциометра П3 и потенциометра обратной связи (ПОС)  = , напряжение на входе усилителя (ПУ) _U = 0, в следствии чего напряжения, подаваемые на тиристорный преобразователь (ТП) _U, двигатель постоянного тока с независимым возбуждением (Д) U_я, отсутствуют; двигатель, приводящий в движение через редуктор (Р) рабочий орган, неподвижен. Рабочий орган механически связан с ползунком ПОС и датчиком скорости – тахогенератором (ТГ). Поэтому углы поворота ПЗ и ПОС -  и  равны. При изменении угла  (например  > ) появляется напряжение _U, полярность и величина которого определяются степенью рассогласования между  и . Возникает соответствующее напряжение U_я, и двигатель вращается, поворачивая рабочий орган (РО) и ПОС и вращая ТГ. ПОС поворачивается таким образом, чтобы угол  стремился(увеличивался) к значению угла . Когда угол  окажется равным новому значению , т.е. когда руль займет новое заданное положение, все напряжения станут равными нулю, поворот рабочего органа и ползунка ПОС прекратится. ТГ необходим для улучшения качества переходных процессов в следящей системе. Алгебраическое суммирование сигналов задания и обратной связи осуществляется при помощи ПЗ и ПОС, а так же тахогенератором ТГ. Оба потенциометра преобразуют углы поворота в напряжения, а оставшийся – угловую скорость, снимаемую с вала Д, в напряжения.

В данной системе к электрической части силового электропривода относятся двигатель (Д); тиристорный преобразователь (ТП), усилитель (ПУ) и редуктор (Р); к элементам систем управления: датчик скорости - тахогенератор (ТГ) и датчики угла поворота (ПЗ) и (ПОС).

Структурная схема сау

На основании принципиальной схемы системы (рис. 1) составляем структурную схему САУ (рис. 2).

M_C

Н_f(p)

Р

α U_З ΔU U_ТП U_Я ω` Δω ω β

ПЗ

ПУ

ТП

Д

ТГ

U_ТГ ω

ПОС

U_ПОС β

Рис.2. Структурная схема САУ

Определение параметров отдельных звеньев сау

Потенциометры задающий (ПЗ) и потенциометр обратной связи (ПОС) являются пропорциональными звеньями с передаточными функциями соответственно:

;

где и - коэффициенты усиления звеньев, которые, исходя из условия, равны ;

Усилитель ПУ также является пропорциональным звеном с передаточной функцией , где К_у – коэффициент усиления данного усилителя. Его значение будет определено из заданной скоростной ошибки.

Тиристорный преобразователь ТП – дискретное звено, с ограниченной полосой пропускания частот управляющего сигнала. Его передаточная функция:

где К_п - коэффициент усиления ТП по напряжению;  - время запаздывания;

Т_п - постоянная времени ТП

;

Двигатель постоянного тока с независимым возбуждением является колебательным звеном при Т_м<4T_я, либо инерционным звеном второго порядка при Т_м>4T_я, где Т_я – электрическая постоянная цепи якоря, Т_м – электромеханическая постоянная времени.

Передаточная функция ДПТ НВ имеет вид:

по заданию

по возмущению

где К_я - коэффициент усиления двигателя при управлении напряжением якоря;

, где

либо ;

Постоянные времени двигателя:

;

;

Так как Т_м>4T_я, то двигатель является инерционным звеном 2-ого порядка.

Характеристическое уравнение двигателя:

,

,

,

; .

,

где ;;,;;

Таким образом для нашей следящей системы передаточная функция двигателя :

по заданию:

,,

по возмущению:

,.

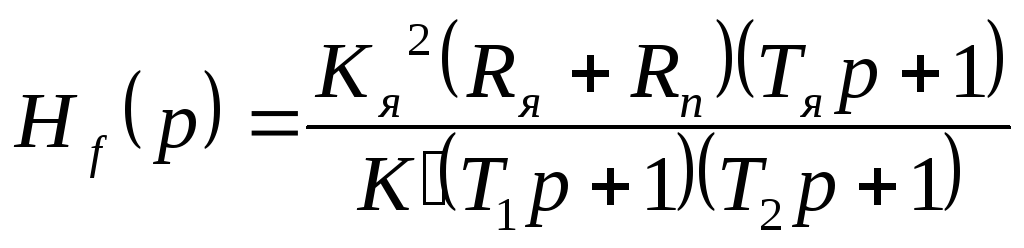Редуктор Р является интегрирующим звеном, т.к. входной координатой является угловая частота , а выходной – угол поворота . Редуктор имеет передаточную функцию:

,

где К_р – коэффициент передачи редуктора, ;

Тахогенератор ТГ является пропорциональным звеном с передаточной функцией:

,

где К_ТГ – коэффициент усиления ТГ, определяемый по условиям устойчивости.

Так как система астатическая, то скоростная ошибка этой системы равна:

,

где К – коэффициент усиления замкнутой системы,

Откуда:

;

,

Уравнение движения САУ

На основании передаточных функций по задающему и возмущающему воздействиям замкнутой системы, записывается уравнение движения этой системы, которое представляет собой дифференциальное уравнение, связывающее выходную координату с задающим и возмущающим воздействиями.

Полное уравнение системы в общем виде в операторной форме имеет вид:

,

где и- передаточные функции по заданию и по возмущению, соответственно.

;

По заданию передаточная функция системы через передаточные функции звеньев выражается:

По возмущению передаточная функция системы через передаточные функции звеньев выражается:

Полное уравнение системы в операторной форме:

где

;

; ,

;

; ,

;

Дифференциальное уравнение 4-го порядка, описывающее систему автоматического управления:

подставляя рассчитанные выше величины получаем: