Лекция 2 Физ_ок

Лекция 2

Уравнения гидротермодинамики в турбулентной жидкости

1. Уравнения движения вязкой жидкости.

2. Правила осреднения.

3. Уравнение неразрывности турбулентной жидкости.

4. Уравнения движения турбулентной жидкости.

5. Уравнение теплопроводности турбулентной жидкости.

6. Уравнение диффузии примеси турбулентной жидкости.

1. Уравнение гидротермодинамики для турбулентной жидкости.

Посмотрим, как будут выглядеть уравнения гидродинамики для турбулентной жидкости. Движение вязкой жидкости описывается с помощью уравнения Навье-Стокса, которые, как и другие балансовые уравнения, является уравнением сохранения, в данном случае количества движения и уравнение неразрывности. Для вязкой несжимаемой жидкости эти уравнения выглядят так:

, .

Поскольку мы считаем жидкость несжимаемой (), то мы нормируем каждый член на , а в принципе в литературе можно встретить и другую запись (например, ).

Форма записи тензорная, т.е. по строкам и по столбцам. Например,

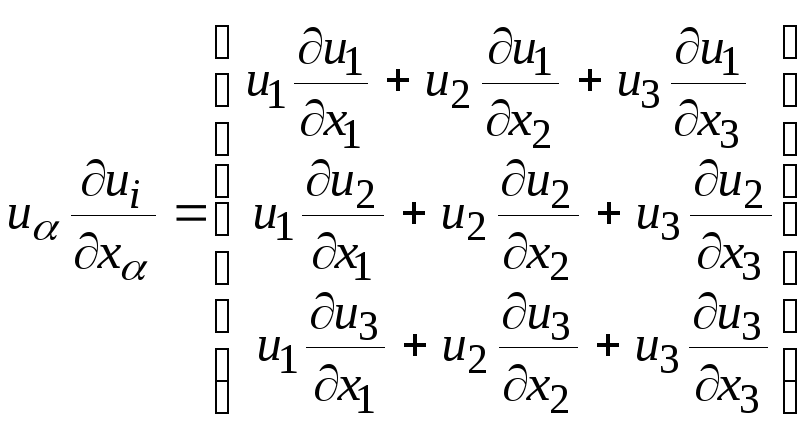
или

,

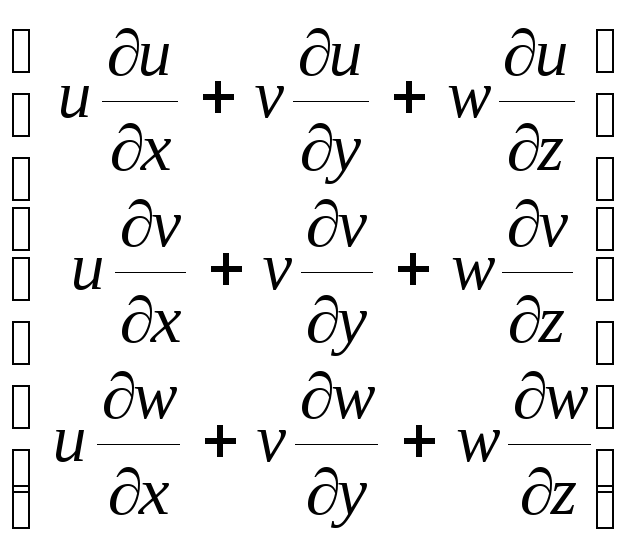где 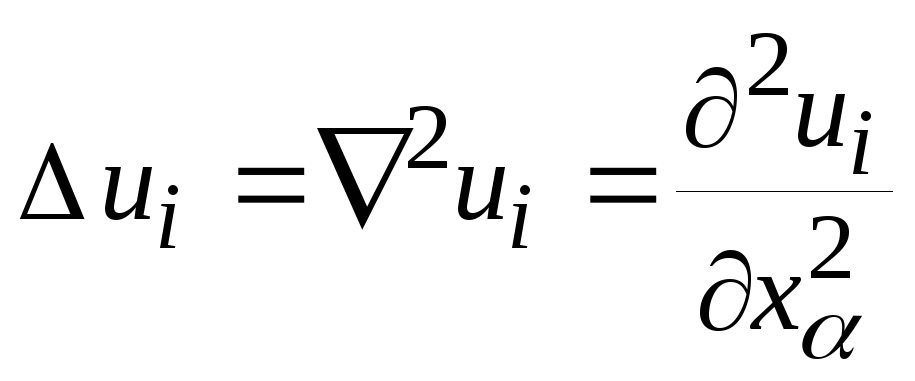- оператор Лапласа.

Физический смысл этого уравнения. Прежде всего, если посмотреть размерность каждого члена, то это будет размерность ускорения. Тогда в левой части этого уравнения будет полное ускорение, а в правой – ускорения, вызванные различными силами и равнодействующая которой, и будет равна полному ускорению. Полное ускорение мы разбиваем на изменение скорости (ускорения) во времени и изменения скорости в пространстве. Т.е., например, для комп. скорости

.

Изменение скорости по пространству вызывается силами инерции, т.е. благодаря этим силам происходит передача количества движения через границы выделенного объема. Поэтому этот член еще называется инерционным или адвективным. В правой части уравнения находятся все остальные силы. Все эти силы делятся на внешние и внутренние. Внутренние силы – это силы, действующие на некоторую точку замкнутой системы со стороны других точек этой же системы. Силы, обусловленные действием материальных точек, не входящих в рассматриваемую систему, называются внешними. К внутренним силам в уравнениях Навье-Стокса относятся силы вязкости или внутреннего трения . Внешние силы также бывают двух типов: массовые и поверхностные. Массовыми называются силы, действие которых на выделенный объем не зависит от присутствия других частей жидкости, а численное значение пропорционально массе этого объема. Например, для моря это сила тяжести, приливообразующая сила, сила Кориолиса. Поверхностными называются силы, приложенные к элементу жидкости со стороны прилегающих к нему частиц остальной части жидкости. Эти силы действуют на поверхность рассматриваемого элемента.

Поверхностная сила, отнесенная к единице площади, на которую она действует, называется напряжением. Всякую поверхностную силу можно разложить на нормальную и касательную к поверхности составляющие. Нормальная составляющая, отнесенная к единице площади (нормальное напряжение) называется давлением , а касательная - касательным напряжением .

Итак, изменение скорости во времени в какой-либо точке вызывается переносом количества движения через границы выделенного объема силами инерций (адвективный член), внешними массовыми силами, которые объединены в один член (иногда выделяют ускорение силы тяжести или ускорение Кориолиса). Ускорение, вызванное нормальной составляющей поверхностных сил (градиентом давления) и силами внутреннего трения. Для того, чтобы получить уравнения движения для турбулентной жидкости воспользуемся еще одним предложением О.Рейнольдса. Он предложил представлять значения всех гидродинамических величин в турбулентном течении в виде суммы осредненных и пульсационных составляющих, т.е. , , , и т.д. Знак « ´ » означает пульсации, т.е. величины, характеризующие отклонения мгновенного значения величины от ее среднего значения. На практике чаще всего необходимо знать только осредненные значения всех величин.

Для того, чтобы произвести осреднение уравнений Навье-Стокса, необходимо выполнить основные правила осреднения, выведенные еще Рейнольдсом:

1) , если ;

2) , если ;

3) ;

4) , если или ;

5) ;

6) , (из уравнения (5), если );

7) ;

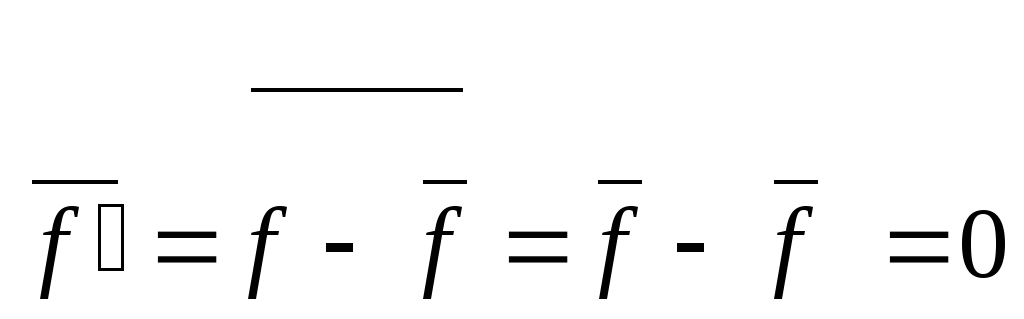8) 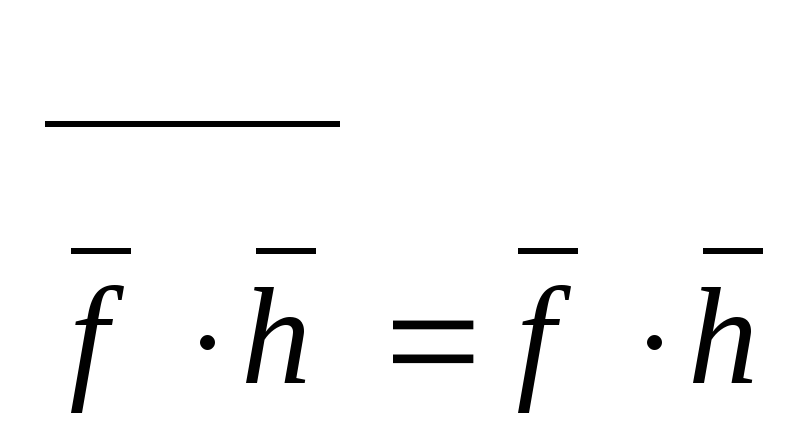, из уравнения (5), если ,

;

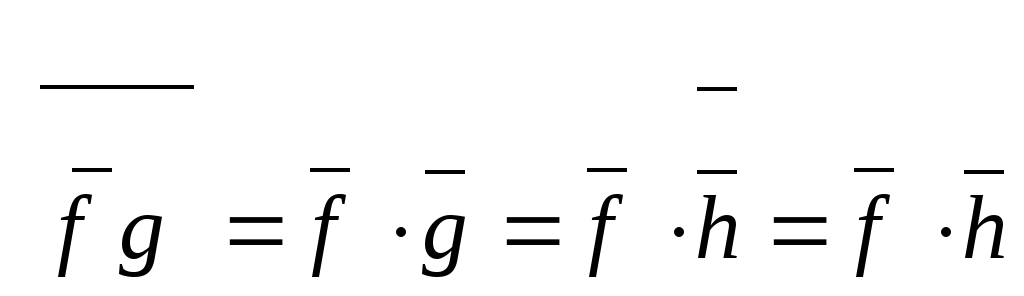9) , из уравнения (5), если ,

;

10) .

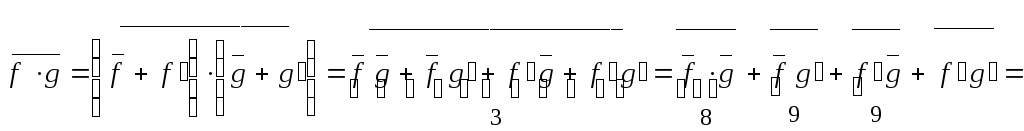
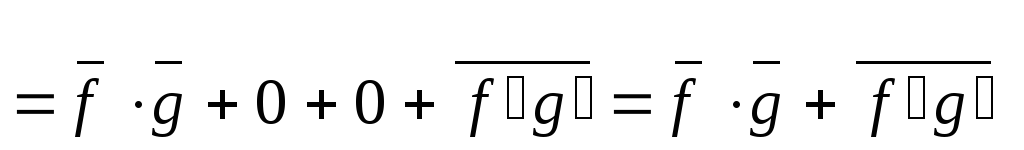Начнем с осреднения уравнения неразрывности

, ,

;

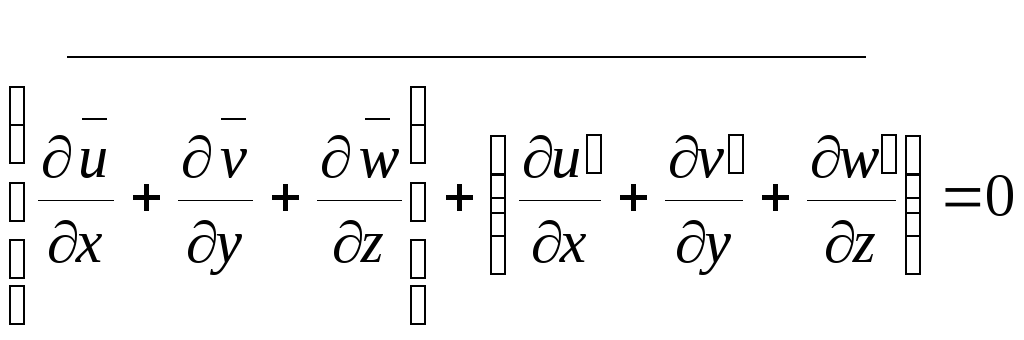Из правила (3) и (4) .

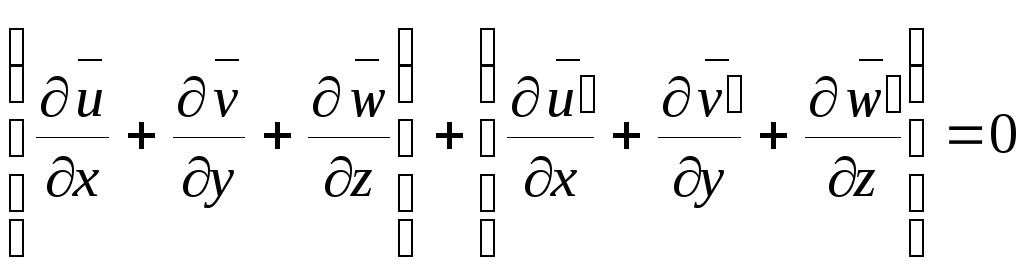Из правила (7) - и .

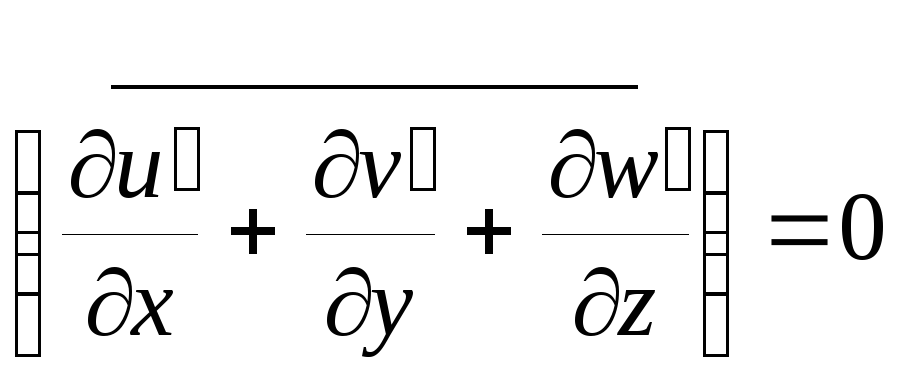Тогда уравнение неразрывности для турбулентной жидкости будет иметь вид

.

Для осреднения уравнений Навье-Стокса возьмем в качестве примера только одно из трех уравнений – проекцию на ось

;

;

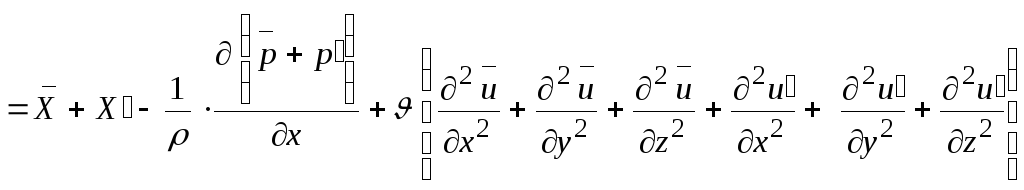По правилу (3), (4) и (7)

.

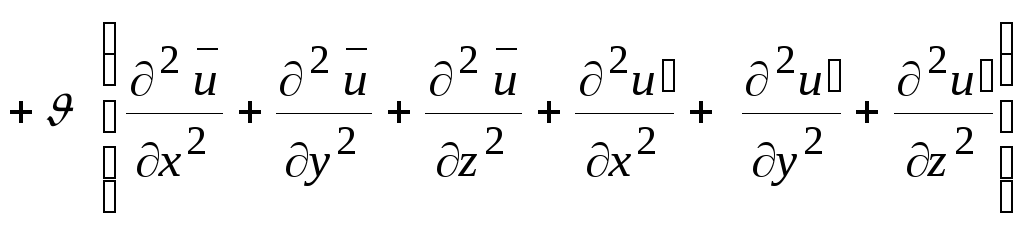По правилу (9)

.

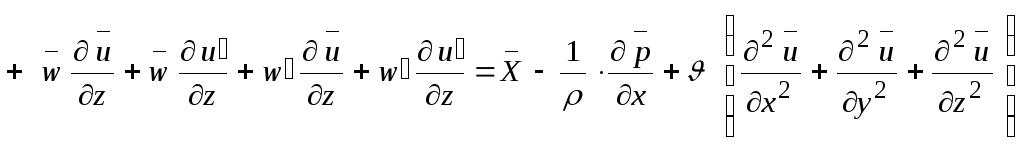По правилу (8)

.

;

;

; .

;

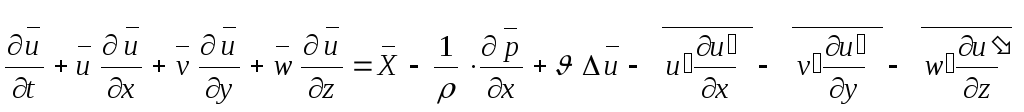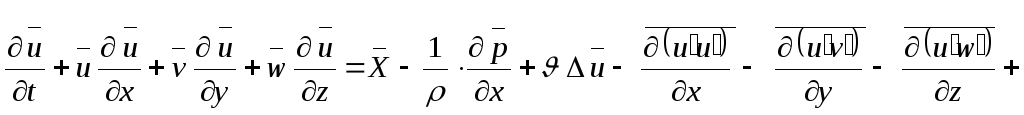
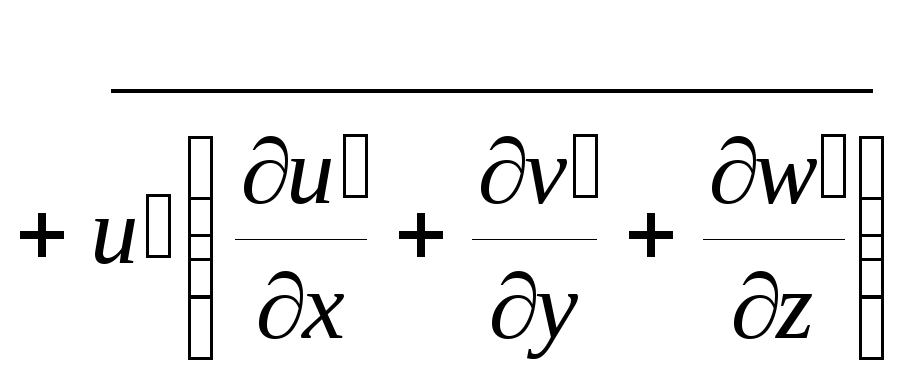Так как из уравнения неразрывности , то получим

.

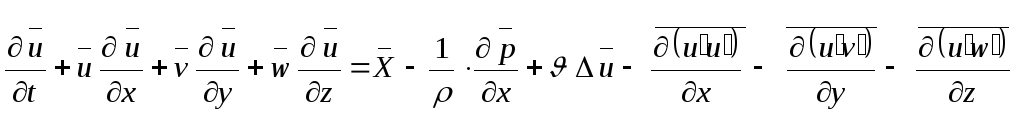Запишем все осредненные уравнения Навье-Стокса в тензорной форме

.

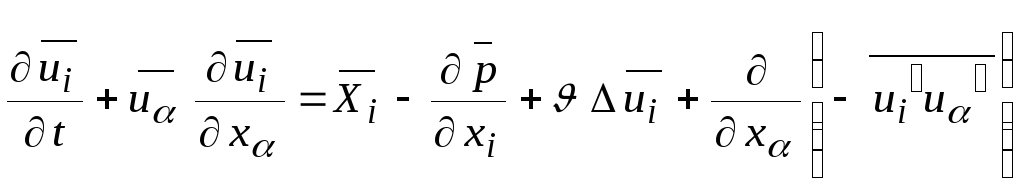Это уравнение называется уравнением Рейнольдса для турбулентного движения несжимаемой жидкости. Оно отличается от уравнения Навье-Стокса наличием дополнительного члена . Умноженный на плотность этот член (или, вернее, члены, их 9) называется напряжением Рейнольдса. Этот член показывает, что в турбулентном потоке обмен количеством движения между элементарными объемами воды обуславливается как силами молекулярной вязкости , так и пульсациями скорости, вызывающими турбулентное перемешивание потока.

Используя тот же прием осреднения, можно получить осреднение уравнения распространения тепла и диффузии пассивной примеси в турбулентном потоке. Уравнение теплопроводности в движущейся жидкости имеет вид

,

где - температура,

- приток тепла от внешних источников,

- коэффициент молекулярной температуропроводности,

- коэффициент молекулярной теплопроводности,

- удельная теплоемкость.

,

где - приток тепла, определяемый фазовыми процессами (испарение, льдообразование),

- диссипация кинетической энергии,

- лучистый поток тепла.

Если умножить каждый член уравнения на и осреднить полученное уравнение, то в результате получим

.

Физический смысл каждого члена следующий:

I – изменение во времени осредненного потока тепла;

II - адвективный перенос тепла осредненным движением;

III - поток тепла за счет молекулярной теплопроводности;

IV - изменение потока тепла от внешних источников;

V - перенос тепла турбулентными вихрями по направлению к отрицательным осям. Его еще называют плотностью турбулентного потока тепла.

Аналогично получаем уравнение турбулентной диффузии примесей. Для молекулярной диффузии это уравнение будет

,

где - концентрация примеси,

- молекулярный коэффициент диффузии.

Проведя преобразования, аналогичные предыдущим, получим

.

Физический смысл составляющих тот же, что и в предыдущем случае:

I - изменение во времени осредненной концентрации примеси;

II - адв ективный перенос примеси;

III - поток примеси за счет молекулярной диффузии;

IV - перенос примеси в результате турбулентных движений или плотность турбулентного потока примеси в направлении, обратном направлению осей координат.