Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесская национальная академия связи им. А.С. Попова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Reference_book_on_Higher_Mathemanics_Part_I_F

.pdf

Скачиваний:

Добавлен:

10.02.2016

Размер:

679.16 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

A function f(x) is decreasing if		f (x1 ) > f (x2 )				whenever x1 < x2
A function f(x) is constant
( f (x) = C ) if		f (x1 ) = f (x2 )				for all x1 and x2

A function f (x) is an even		f (− x) = f (x) for x D(x) and − x D(y)
function
A function f (x) is called an odd		f (− x) = − f (x) for x D(x) and − x D(y)
function if
A function f (x) is a periodic		f (x + P) = f (x) for x D(x)
function with period P if
Composite function		f (g(x)) − function of function

The graphs of the given function	f (x) and its inverse f −1 (x) are symmetric one to
other with respect to the line y = x.

Linear function		y = ax + b

Quadratic function		y = ax 2 + bx + c
The graph of a quadratic function		parabola
Standard form of a quadratic		y = a(x − x0 )			2	+ y0
function		y = a(x − x0 )				+ y0
function
Hyperbola		y =	a	, n N
			a

			x n
An exponential function		y = a x , a > 0, a ≠ 1
Logarithmic function		y = loga x , a > 0, a ≠ 1

Table for Finding the Domain of a Composite Function

y =

(

)

(

)

(

)

(

)

(

)

2k f (x)

tan f

cot f

arcsin f

loga f

x ,

g(x)

arccos f (x)

D(y ):

g(x) ≠ 0

f (x) ≥ 0

f (x) > 0,

f (x)

≠ π + πn,

f (x) ≠ πn,

f (x)

≤ 1

a > 0, a ≠ 1

n Z

A.Graphs in the Cartesian System of Co-ordinates

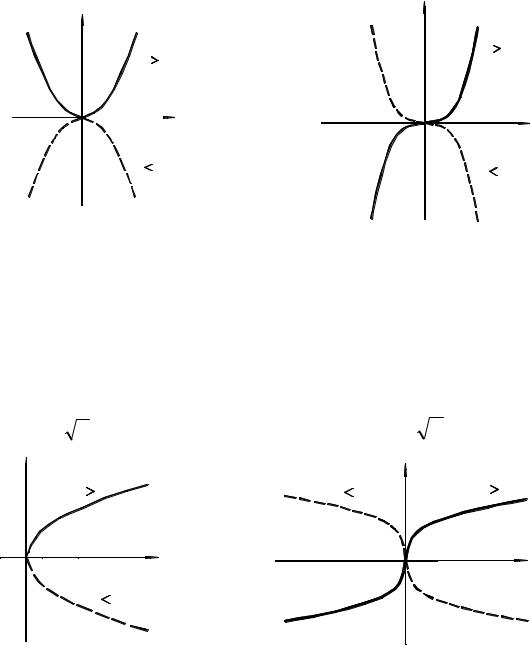
I.Power Functions

1. Parabolas

a). y = ax2n , n = 1,2,K
y
a	0
	x
0
a	0

Domain of definition:

D(y) = (− ∞,+∞)

Range of values

[0, ∞), a > 0

E(y) = (− ∞ ] <

,0 , a 0

b). y = ax2n+1 , n = 1,2,K
y
a	0
	x
0
a	0
D(y) = (− ∞,+∞)

E(y) = (− ∞,+∞)

c). y = a2 n x , n = 1,2,L
y
a	0
		x
0
	a	0

d). y = a 2 n +1 x , n = 1,2,L
a 0	y	a	0
a 0		a	0
			x
	0

D(y) = [0,+∞)	D(y) = (− ∞,+∞)
E(y) = [0,+∞), a ≥ 0	E(y) = (− ∞,+∞)
E(y) = [0,+∞), a ≥ 0
(− ∞,0], a ≤ 0

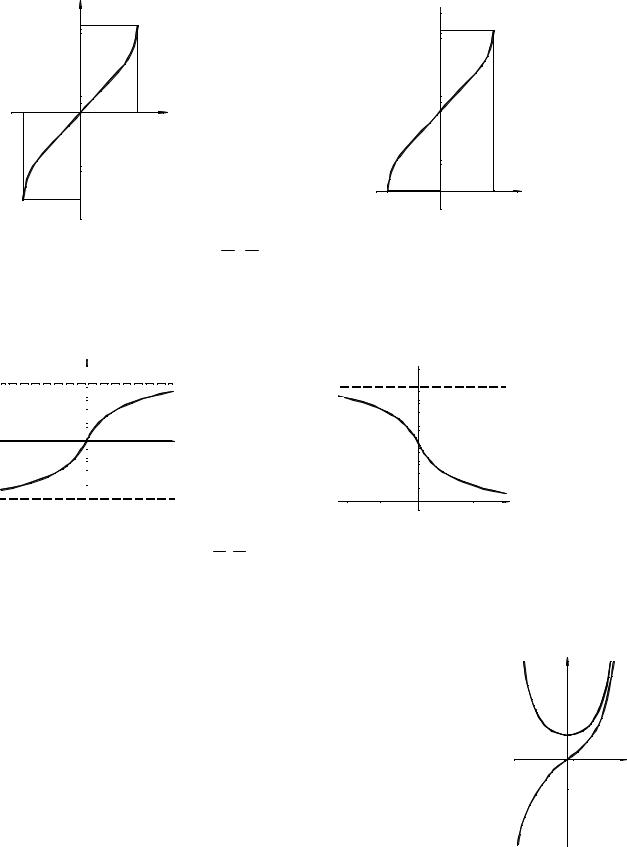
2. Hyperbolas

a). y =	a	, n	= 1,2,K
a). y =	x 2n−1	, n	= 1,2,K
	x 2n−1
			y
	a 0		a	0
			0
D(y) = (− ∞,0) (0,+∞)

E(y) = (− ∞,0) (0,+∞)

II. Exponential Function

y = a x , a > 0, a ≠ 1
y
	a	1
1	0	a	1
			x
0
D(y) = (− ∞,+∞)

E(y) = (0,+∞)

b). y =	a	, n = 1,2,K
	x 2n
	y
		a	0
			x
	0
		a	0

D(y)= (− ∞,0) (0,+∞)

(0,+∞), a > 0

E(y) = (− ∞ ) <

,0 , a 0

III. Logarithm Function

y = log a		x, a > 0, a ≠ 1
y
		a	1
					x
0	1
			0	a	1

D(y) = (0,+∞)

E(y) = (− ∞,+∞)

IY. Trigonometric Functions

1). Sinusoid (sine curve, harmonic curve) y = sin x

		y		D(y) = (− ∞,+∞),
		1		D(y) = (− ∞,+∞),
				E(y) = [−1,+1]
				x
-π	π	0	π	π
	---		--
	2		2
		-1
2). Cosine curve		y = cos x
		y
		1		D(y) = (− ∞,+∞),
				D(y) = (− ∞,+∞),

x	E(y) = [− 1,+1]

-π	π	0	π	π
	---	0	--
	2		2
		-1
3). Tangent curve		y = tan x

		y
						−	π	π
					D(y) =	−		+ kπ ,	+ kπ , k = 0,±1,±2,K
							2	2
				x	E(y ) = (− ∞,+∞)
				x
-π	π	0	π	π
	---	0	--
	2		2
4). Cotangent curve			y = cot x
		y			D(y) = (kπ , (k + 1π )), k = 0,±1,±2,K
					D(y) = (kπ , (k + 1π )), k = 0,±1,±2,K
				x	E(y) = (− ∞,+∞)
-π	π	0	π	π
	---	0	--
	2		2

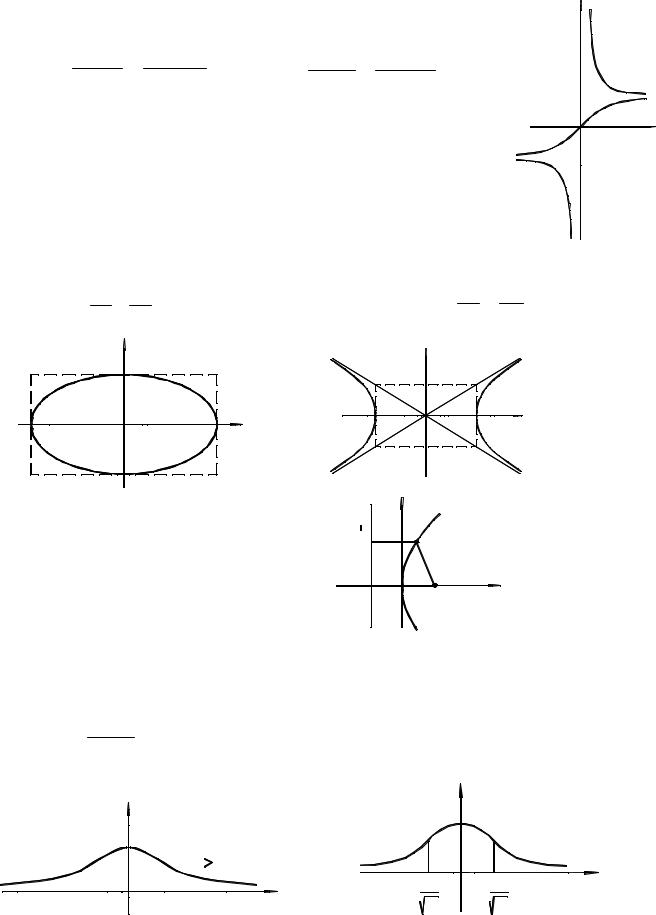
Y. Inverse Trigonometric Functions

1). y = sin −1 x = arcsin x
				y
				π
				--
				2
-1							x
				0			1
					π
				---
					2
D	(	y	)	[	]		E(y) =	− π		,	π
D		y		= −	1;1	,
									2		2

3). y = tan −1 x = arctan x
y
π
--
2
x
0
π
---
2
	π	π
D(y ) = (− ∞,+∞), E(y) = −	,
	2	2

2). y = cos −1 x = arccos x
	y
	π
	π
	--
	2
		x
-1	0	1
D(y) = [− 1;1], E(y) = [0;π ]

4). y = cot −1 x = arc cot x

D(y ) = (− ∞,+∞), E(y) = (0,π )

YI. Hyperbolic Functions
1). y = sinh x (shx)		2). y = cosh x (chx)
sinh x =	e x − e− x	cosh x =	e x + e − x
	2		2

D(sinh x) = (− ∞,+∞)		D(cosh x) = (− ∞,+∞)
E(sinh x) = (− ∞,+∞)		E(cosh x) = [1,+∞)

y=chx

y=shx

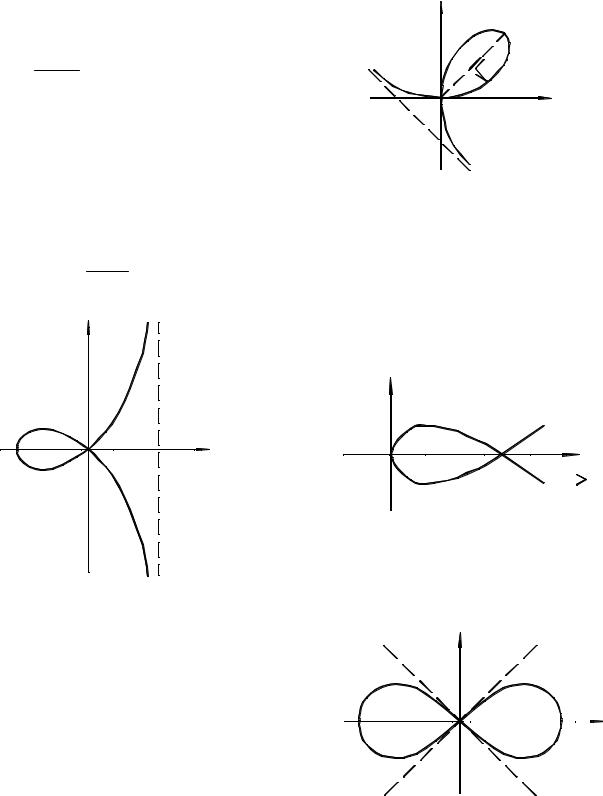
3). y = tanh x

(thx)

4). y = coth x

(cthx)

tanh x = sinh x = e x

− e− x

coth x = cosh x = e x + e − x

y=cthx

cosh x

e x

+ e− x

sinh x

e x − e − x

D (tanh x ) = (− ∞ ,+∞ )

D(coth x) = (− ∞,0) (0,+∞)

y=thx

E(tanh x) = (− 1,+1)

E(coth x) = (− ∞,−1) (1, ∞)

y=cthx

YII. Curves of the Second Order

x 2

y 2

x 2

y 2

1. Ellipse: a 2

+ b 2 = 1

2.Hyperbola:

a 2

− b 2

= 1

-a

-b

y 2 = 4 px

3. Parabola

F (0,

4. Witch of Agnesi:

y =

1 + x 2

	y
	k
		k	0
			x
-1	0	1

5.Curve of Gauss:

y = e− x2
		y
		1
			x
-	1	0	1
-	2		2
	2		2

6. Loops

a). Folium of Descartes

x3 + y 3 − 3axy = 0 , or

3at

1 + t 3x =

	3at 2

y =
	1 + t	2

b)	y 2	= x 2 a + x
		a − x
		y
-a		a	x
		0

7. Lemniscate of Bernoulli

(x 2 + y 2 )2 = a 2 (x 2 − y 2 )

r 2 = a 2 cos 2ϕ

	y
	a
	3	2
		2	x
			x
x	0
+
	y
	+
	a
	=
	0

c). a 2 y 2 = x(a − x 2 ), a > 0

	y
		x
0	a	a	0
		a	0

	y
	x
0	a
0

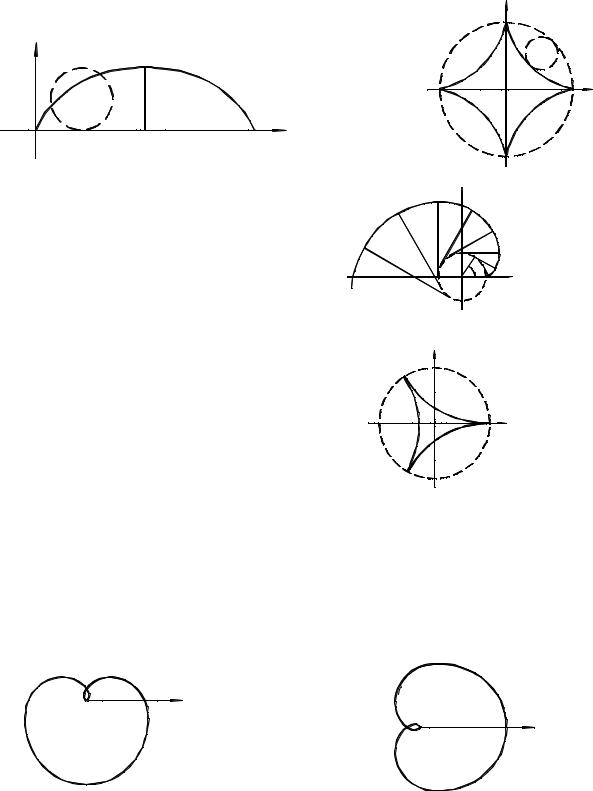
B. Curves Given by Parametric Equations

I. Cycloid:

x = a(t − sin t )
	, a > 0
y = a(1	− cost )

	2 a
	x
0	2π a

III. Evolvent of Circle:

x = a(cos t + t sin t )

, a > 0

= a(sin t − t cos t )

IY.

x = R cos

+ cos

y = R sin

− sin

		3	t
x = a cos			t
II. Astroid:	3		, a > 0
			t
y = a sin			t

	y
	a
-a	a	x
	0
	-a

y
a
t	x
0

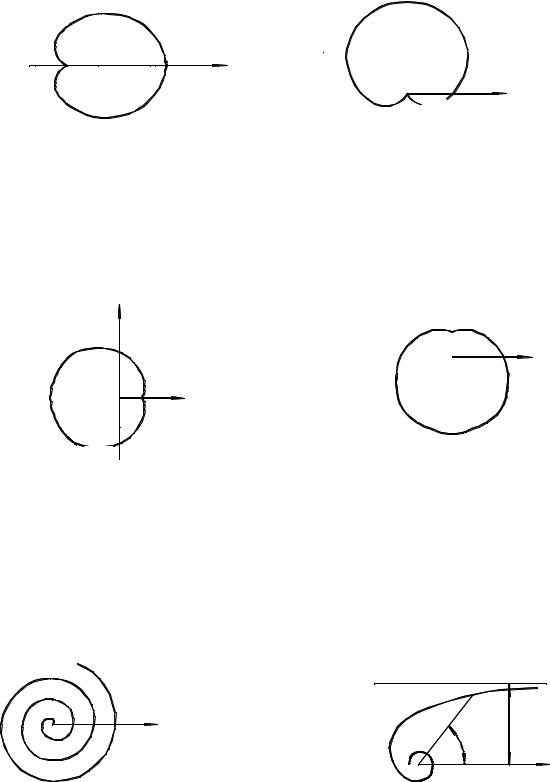
C. Curves in the Polar System of Coordinates

1. ρ = a sin	3	ϕ		II. ρ = a cos				3	ϕ ,
			,
		3	,
		3
a > 0,ϕ [0,3π ]					3π		3π
				a > 0,ϕ −		,
				a > 0,ϕ −		,
					2		2

	III. Cardioids
1) ρ = a(1 + cosϕ ), a > 0	2) ρ = a(1 + sin ϕ ), a > 0

	2 a
0	ρ	0
0		0

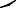
a ρ

IY. Limacons

`1). ρ = a − cosϕ , a > 1

2). ρ = a − sinϕ , a > 1

	Y. Spirals
1). ρ = aϕ, a > 0	2). ρ =	a	, a > 0

	ϕ

0		M
0	ρ	a
ρ		ϕ
		ϕ
0		ρ

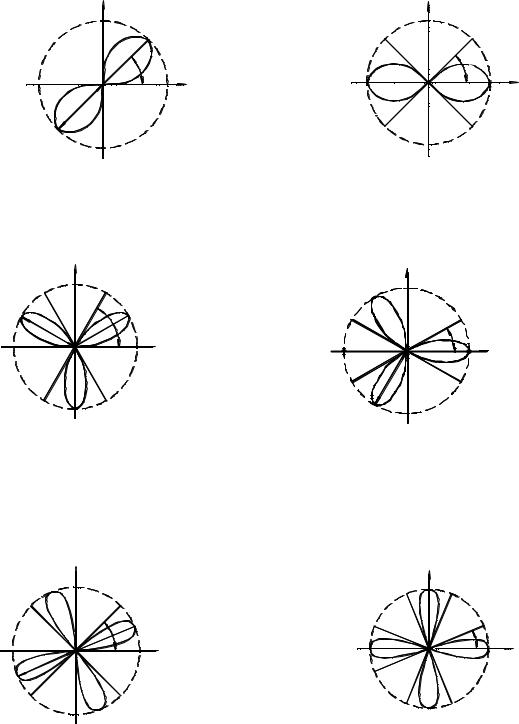
1). ρ = a sin 2ϕ , a > 0
y
π
--	x
4	x
0	ρ
a

3). ρ = a sin 3ϕ, a > 0
y
π
--
3
a	x
	x
0	ρ

YI. Roses

2). ρ = a cos 2ϕ , a > 0
y
π
--
4
a	x
0	ρ
0

4). ρ = a cos 3ϕ , a > 0
y
	π
	-
	6	x
		x
0		ρ
0
a

5). ρ = a sin 4ϕ, a > 0

6). ρ = a cos 4ϕ , a > 0

		y	y
			y
		π
		--	π
		4	π
		4	--
			8
		x	a	x
a	0	ρ	0	ρ
		ρ

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.11.20181.48 Mб10RAZDYeL_1.doc
#
23.11.20181.1 Mб13RAZDYeL_2.doc
#
23.11.2018443.39 Кб6RAZDYeL_3.doc
#
01.05.202575.26 Кб0ref-23022.doc
#
01.05.202581.92 Кб0ref-23022.doc
#
10.02.2016679.16 Кб6Reference_book_on_Higher_Mathemanics_Part_I_F.pdf
#
10.02.2016112.51 Кб49REGIONAL_NA_EKONOMIKA.docx
#
01.04.20251.16 Mб0Rozdil_3.doc
#
01.04.2025327.17 Кб0Rozdil_5.doc
#
01.04.2025259.07 Кб0Rozdil_7.doc
#
05.05.20191.58 Mб2RPS_Kovalevskiy.doc