2.6 Спектральний аналіз неперіодичних сигналів

Співвідношення

і(2.43)

становлять пару перетворень Фур’є–прямейзворотнеперетворення. ФункціяS(j) називаєтьсяспектральною густиноюсигналу. У загальному випадку спектральна густинаS(j) є комплексною функцією. Вона визначається на інтервалі (,). Представимо її через модуль і аргумент.

Функція S() називаєтьсяамплітудним спектромсигналу, а функція() –фазовим спектромсигналу. ФункціяS() – парна функція частоти, тому зазвичай на графіках цю функцію зображують для невід’ємних частот (рис. 2.15). Ширину спектра неперіодичного сигналуF_maxвизначають аналогічно визначенню ширини спектра періодичного сигналу.

Багато сигналів мають парну симетрію (це досягається шляхом відповідного вибору початку відліку часу). У таких сигналів спектральна густина – дійсна функція

. (2.44)

Внаслідок парності функції S() зворотне перетворення Фур'є

. (2.45)

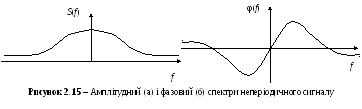
Останні два інтеграли становлять пару косинус-перетворень Фур'є.

Принципова відмінність спектрів полягає в тому (рис. 2.10 і 2.15), що у неперіодичного сигналу спектр суцільний, ау періодичного – дискретний, він містить гармоніки частотиf₁= 1/T.

Перехід від ряду Фур'є до перетворення Фур'є здійснюють шляхом припущення, що неперіодичний сигнал є умовно періодичним з періодом Т →, тоді частота вже не є дискретною і стає неперервним параметром перетворення (2πnf₁→ω), знак суми переходить в знак інтегралу.

У ряді випадків корисним є використання дельта-функції (одиничного імпульсу) (t). Спектральна густина дельта-функції(t–t₀)

, приt₀= 0(j) = 1.(2.46)

Використовується також дельта-функція у частотній області ( – ₀), зворотне перетворення Фур’є якої

. (2.47)

Тобто, 2(–₀) є спектральною густиною комплексної експоненти .

Використовуючи наведені вище властивості дельта-функції, можна знайти спектральну густину гармонічного коливання s(t) =Acos(₀t+₀)

. (2.48)

Таким чином, використання дельта-функції дозволяє визначати спектральну густину періодичного сигналу, який не задовольняє умові абсолютної інтегруємості.

Апарат перетворення Фур'є є досить ефективним математичним засобом для розв’язання багатьох задач теорії й техніки зв’язку. Відзначимо лише деякі найбільш використовувані властивості перетворення Фур'є.

1. Добуток двох сигналів (загальний випадок):

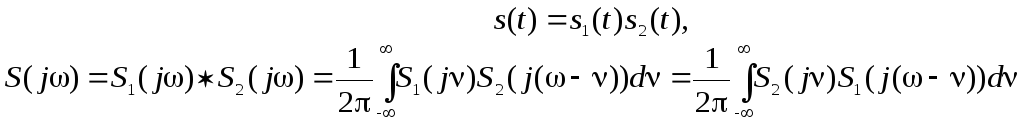(2.49)

– множенню сигналів у часовій області відповідає згортка їхніх спектрів.

2. Згортка сигналів

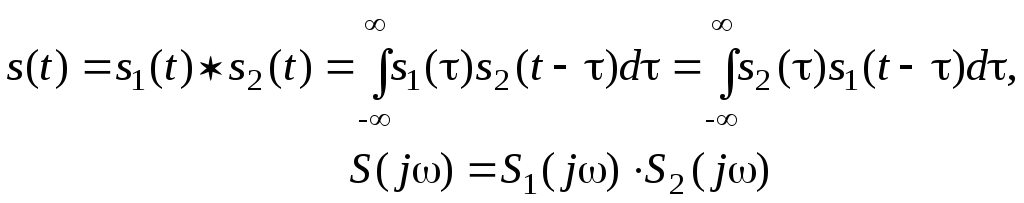(2.50)

– згортці сигналів у часовій області відповідає множення їхніх спектрів.

3. Розрахунок енергії сигналів

(2.51)

– це співвідношення називається рівністю (теоремою) Парсеваля для перетворення Фур'є.

4. Скалярний добуток сигналів:

. (2.52)

Прирівнюючи останнє співвідношення до нуля, отримаємо умову ортогональності сигналів, заданих спектральними густинами.

5. Спектральна густина суми сигналів дорівнює сумі спектральних густин цих сигналів(перетворення Фур'є є лінійним):

;. (2.53)

Приклад 2.7.Нехай сигнал– постійна напруга, її спектральна густина описується виразом(рис. 2.16,а),– гармонічне коливання, спектральна густина якого наступна(рис. 2.16,б). Враховуючи лінійність перетворення Фур'є, спектральна густина суми заданих сигналів буде наступною(рис. 2.16,в).

Вправа 2.6.Доведіть співвідношення (2.53).

6. Затримка сигналу в часі призводить до зміни фазового спектра сигналу і не змінює його амплітудний спектр:

;. (2.54)

Якщо окремо розглянути амплітудний та фазовий спектри, то отримаємо

або,.

Приклад 2.8.Нехай сигналs₁(t) – П-імпульс тривалості(рис. 2.17,а), амплітудний спектр якогоS(f ) є модулем функції видуsinx/x(рис. 2.17,б), а фазовий спектрφ(f) набуває значення 0 в непарних пелюстках і –π в парних (рис. 2.17,в). Продемонструємо властивість затримки сигналу в часі.

Нехай затримка імпульсу складає чверть його тривалості τ/4 (рис. 2.17, г). Тоді до частоти 1/τ функціяφ(f) буде лінійно збільшуватись до значення 2π(1/τ)(4/τ) = π/2 (рис. 2.17,д). В діапазоні частот (1/τ, 2/τ) до лінійної залежності додасться значення –π і т.д. Якщо імпульс не затримується, а випереджає (рис. 2.17,е), то його фазовий спектр є зростаюча залежність (рис. 2.17,є).

Вправа 2.7.Доведіть співвідношення (2.54).

7. Зміна масштабу сигналу в часі призводить до оберненої зміни масштабу спектральної густини:

;. (2.55)

Тобто, якщо сигнал стиснути в часі в аразів (а > 1), то його спектральна густина розтягнеться вздовж осі частот, а рівень складових зменшиться у стільки ж разів. І навпаки, розтягування сигналу в часі (а < 1) призводить до стискання спектральної густини вздовж осі частот і збільшення рівня її складових.

Приклад 2.9.Нехай сигналs₁(t)– П-імпульс тривалості τ₀(рис. 2.18,а). З попереднього прикладу відомо, що амплітудний спектр П-імпульсу є модулем функції виду(рис. 2.18,б). Продемонструємо властивість зміни масштабу сигналу у часі.

Нехай сигнал стиснено в часі удвічі (а = 2) (рис. 2.18,в), тоді всі складові амплітудного спектра отримають множник 0,5, а їх частоти збільшаться удвічі (рис. 2.18,г). Як видно з рисунку, характерна точка – перший нуль спектральної густини тепер знаходиться не на частоті 1/τ₀, а на частоті 2/τ₀.

Нехай сигнал розтягнуто в часі у двічі (а = 1/2) (рис. 2.18,д), тоді всі складові амплітудного спектра отримають множник 2, а їх частоти навпаки зменшаться удвічі (рис. 2.18,е).

Вправа 2.8.Доведіть співвідношення (2.55).

8. Множення сигналу на гармонічне коливання призводить до зміщення його спектра на частоту цього коливання(як у від'ємній, так і додатній областях частот):

;. (2.56)

П

в

г

риклад 2.10.Нехай сигналs₁(t) – П-імпульс (рис. 2.19,а,б). Продемонструємо властивість множення сигналу на гармонічне коливання.

На рис. 2.19, впобудовано графік гармонічного коливання cos2πf₀t, відповідно до виразу (2.48) на рис. 2.19,гпобудовано амплітудний спектр цього коливання. В результаті множення П-імпульсу на гармонічне коливання отримуємо відрізок гармонічного коливання – радіоімпульс (рис. 2.19,д), спектр якого складається з двох копій спектраS₁(f) центрованих відносно частот –f₀іf₀з удвічі меншими амплітудами складових.

Вправа 2.9.Доведіть співвідношення (2.56).

Рисунок 2.19 – До пояснення властивості перетворення Фур'є сигналу, помноженого на гармонічне коливання

9. Множення сигналу на комплексне гармонічне коливання призводить до зміщення його спектра на частоту цього коливання в додатній або від'ємній області частот:

;. (2.57)

Приклад 2.11.Нехай сигналs₁(t) – П-імпульс (рис. 2.20,а,б). Продемонструємо властивість множення сигналу на комплексне гармонічне коливання.

На рис. 2.20, впобудовано графік комплексного гармонічного коливання, яке відповідно до формули Ейлера складається з дійсної частини –гармонічного коливанняcos(2πf₀t) й уявної –sin(2πf₀t). Відповідно до виразу (2.44) на рис. 2.20,гпобудовано амплітудний спектр цього коливання. В результаті множення П-імпульсу на отримуємо комплексний радіоімпульс (рис. 2.20,д), спектр якого є копією спектраS₁(f), центрованого відносно частотиf₀. Оскільки кількість спектральних складових залишилась незмінною, то, відповідно, амплітуди складових також незмінні.

Вправа 2.10. Доведіть співвідношення (2.57).

Рисунок 2.20 – До пояснення властивості перетворення Фур'є сигналу, помноженого на комплексне гармонічне коливання