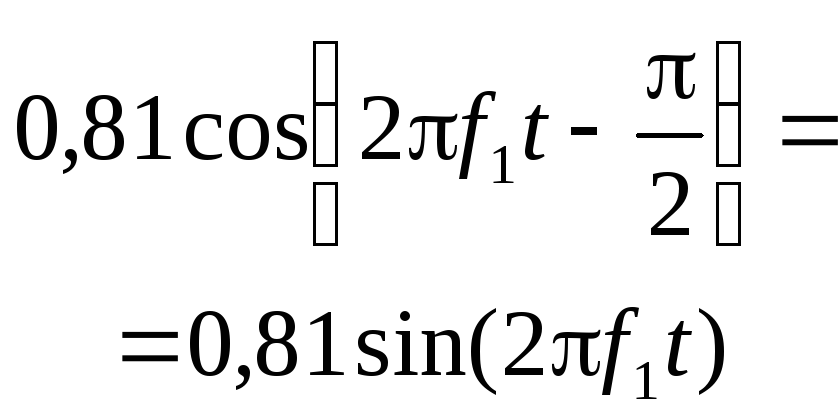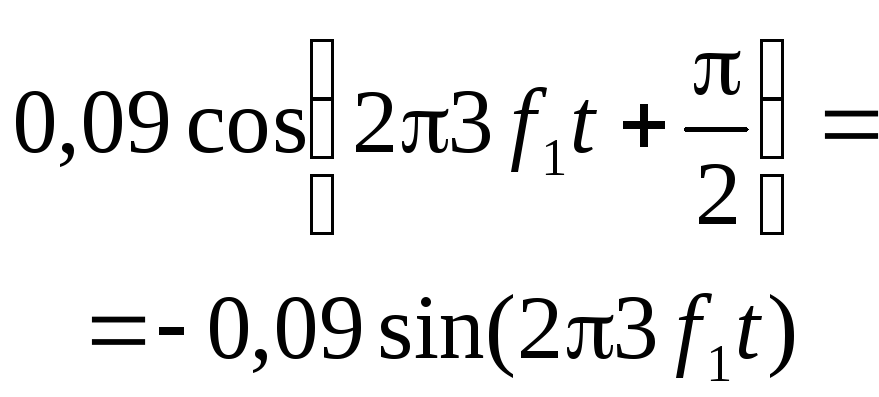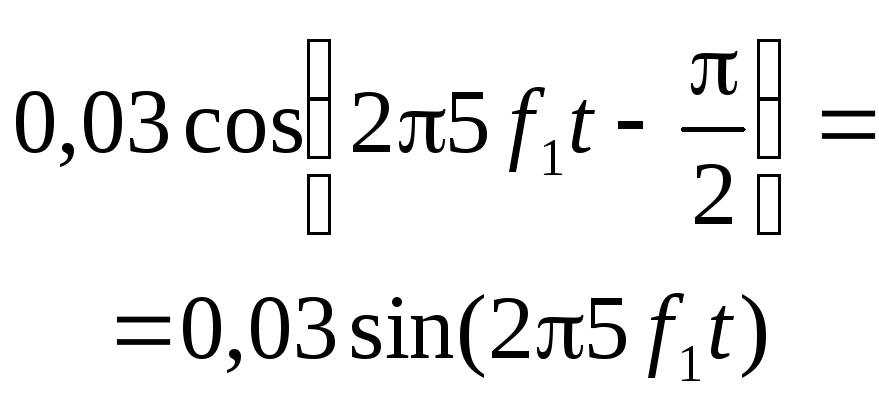2.4 Геометричне подання сигналів

При математичному описі сигнали зручно розглядати як такі, що належать деякому N-вимірному простору. Тоді кожний із сигналів відображається вектором або точкою в цьому просторі (рис. 2.8) (точка – це кінець вектора). Згадаємо, що вектор – це відрізок заданого напрямку й довжини. Звичайно вектор задають координатами його кінця. Зрозуміло, що повинна бути задана система координат. Вона задається ортами – векторами одиничної довжини, кути між якими дорівнюють 90. Отже, сигналуs(t) ставиться у відповідність вектор.

Основні співвідношення для N-вимірного лінійного метричного простору:

– норма (довжина)вектора

=; (2.31)

– відстань між векторами й

; (2.32)

– скалярний добуток векторів і

. (2.33)

Функціональним просторомназиваєтьсясукупність всіх функцій часу, заданих на інтервалі (0, T_s). Ці функції розглядаються як вектори у функціональному просторі. Координатами цих векторів є значення самих функцій часу. Ясно, щоN∞, а співвідношення (2.31)…(2.33) переходять у наступні:

– норма (довжина) вектора

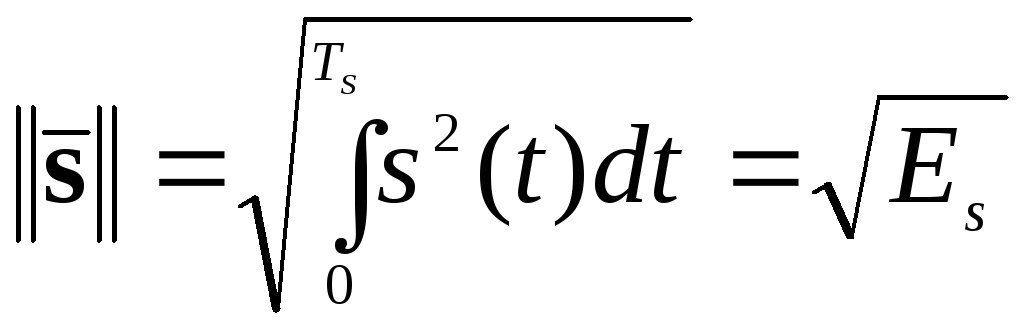, (2.34)

важливо пам'ятати, що довжина вектора дорівнює кореню з енергії сигналу;

– відстань між векторами й

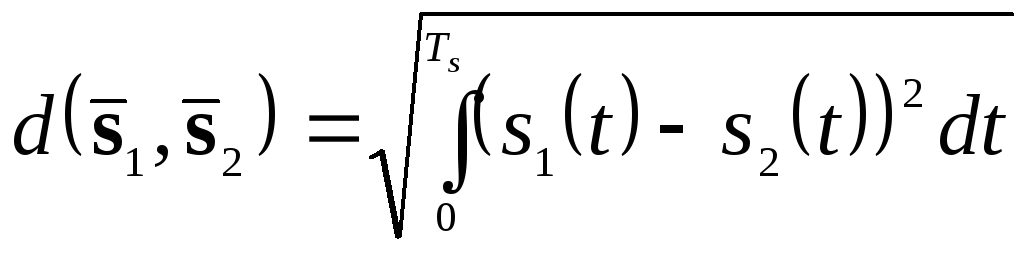; (2.35)

– скалярний добуток векторів і

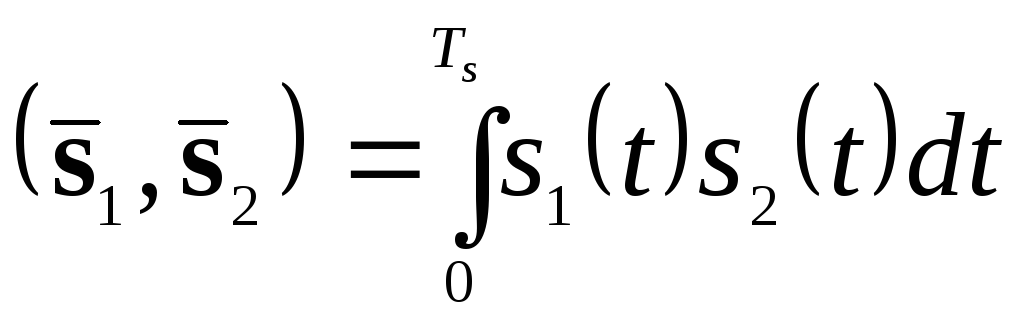. (2.36)

Звернемося до розкладання сигналів в узагальнений ряд Фур'є:

. (2.37)

Вважаємо, що базисні функції ортогональні й нормовані, і їх можна вважати ортами . Перепишемо співвідношення у векторній формі

. (2.38)

Отже, якщо сигнал розкласти в узагальнений ряд Фур'є, то він може бути представлений в N-вимірному просторі.

Приклад 2.4. Нехай гармонічні коливання описуються виразамиі, а. Доведемо, що ці коливання є ортогональними на інтервалі (0,Т), та зобразимо їх векторами.

Два сигнали є ортогональними, якщо їх скалярний добуток дорівнює нулю. Обчислимо скалярний добуток та енергії сигналів:

;.

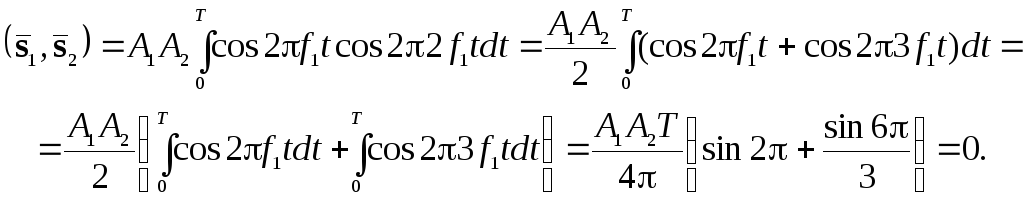
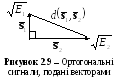
Отже, сигнали є ортогональними і зображаються взаємно перпендикулярними векторами довжин івідповідно (рис. 2.9).

Вправа 2.3.Задано сигналиі. Доведіть їх ортогональність.

Приклад 2.5.Знайдемо відстань між сигналами, заданими у прикладі 2.4.

Використаємо вираз (2.35):

2.5 Спектральний аналіз періодичних сигналів

Для розкладання сигналів у ряди найбільш широке застосування в теорії й техніці зв’язку має тригонометричний базис (базисними функціями є гармонічні коливання). Широке застосування гармонічних коливань у теорії й техніці зв’язку обумовлене тим, що при проходженні через лінійні електричні кола форма кожної з них не змінюється – змінюються лише їхні амплітуди й фази (з’являється зсув у часі).

Ряд Фур’є для періодичного сигналузаписується

. (2.39)

де f₁= 1/T,T– період сигналуs(t);

.

Якщо ввести позначення

,,

то ряд (2.36) набуде виду

. (2.40)

Розкладання сигналу (2.39) і (2.40) називають рядом Фур’є в тригонометричній формі. Більш зручно користуватися рядом (2.40), оскільки він безпосередньо встановлює, з яких гармонічних складових складається сигнал – які значення їхніх частотnf₁, амплітудА_nі початкових фаз_n. Ряд (2.40) визначає спектр сигналу(синонімом слова "спектр" є "складові").

Наочне представлення про спектр сигналу (2.40) дають два рисунки, на яких будують амплітудний спектр– залежність амплітудА_nвід частоти йфазовий спектр– залежність початкових фаз_nвід частоти. Частотаf₁називаєтьсяосновною частотоюсигналу, вона дорівнює числу періодів сигналу за секунду. Гармонічні коливання частотnf₁(n= 2, 3, ...) називаютьгармонікамичастотиf₁: коливання частоти 2f₁– 2-га гармоніка, коливання частоти 3f₁– 3-тя гармоніка й т.д. Приклад амплітудного спектра деякого сигналу наведено на рис. 2.10.

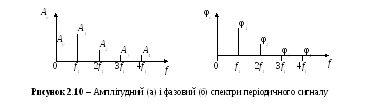
Амплітудний спектр дозволяє визначити ширину спектрасигналу F_max, як протяжність області частот, куди потрапляють складові, сумарна енергія яких становить певну частку від повної енергії сигналу (наприклад, 95% або 99%). В інших випадках ширину спектра визначають як протяжність області частот, поза якою амплітуди складових не перевищують деяке задане значення (наприклад, 0,05 від максимального значення середА_n). Якщо спектр сигналу, що розглядається, примикає до нульової частоти, то ширину спектра сигналу виражають числомF_max. ВизначившиF_max, вважають, що сигнал не містить коливань, частоти яких вищіF_maxу тому розумінні, як цеоговоренов умові визначення ширини спектра.

Спектральне подання періодичного сигналу можна виконати, використовуючи експонентні базисні функції

,n= ..., –1, 0, 1, 2, ... .

При цьому ряд записується

. (2.41)

Таке розкладання сигналу називається рядом Фур'є в комплексній формі.

Коефіцієнти розкладання визначаються

,n= ..., –1, 0, 1, 2, ... . (2.42)

Легко переконатися, що

.

Особливістю ряду Фур'є в комплексній формі єкомпактний запис ряду й коефіцієнтів розкладання. Іншою особливістю євикористання від’ємних частот.

Спектри, що відповідають ряду (2.41), називаються двосторонніми. Дільник 2 в останньому виразі пов'язаний саме з тим, що двосторонній спектр містить удвічі більше складових.

Приклад 2.6. Задано шість коефіцієнтів розкладання деякого сигналу у ряд Фур'є в комплексній формі (табл. 2.1). Визначимо за цими коефіцієнтами амплітудний і фазовий спектри та побудуємо їх (табл. 2.1, рис. 2.11, рис. 2.12).

Виконаємо синтез сигналу, а синтезований сигнал подамо графіком в межах двох періодів.

Таблиця 2.1– Коефіцієнти розкладання сигналу в ряд Фур’є

п	0	1	2	3	4	5
	0		0		0
, В	0	0,81	0	0,09	0	0,03
, рад	–		–		–

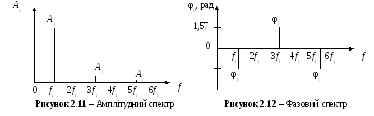
Вирішуємо задачу синтезу. Для цього спочатку на інтервалі визначимо значення складових тригонометричного ряду Фур'є з урахуванням визначених раніше амплітудного і фазового спектрів.

Таблиця 2.2– До розв’язання задачі синтезу сигналу

	0
	0	0,41	0,70		0,81	0,70	0,41	0	–0,41	–0,70	–0,81	–0,70	–0,41	0
	0	–0,09	0		0,09	0	–0,09	0	0,09	0	–0,09	0	0,09	0
	0	0,02	–0,03		0,03	–0,03	0,02	0	–0,02	0,03	–0,03	0,03	–0,02	0
	0	0,33	0,67		0,93	0,67	0,33	0	–0,33	–0,67	–0,93	–0,67	–0,33	0

За табл. 2.2 будуємо графік сигналу s(t) (рис. 2.13). Спочатку будуємо на інтервалі(0, T)і те ж саме повторюємо на інтервалі(–T, 0). З рисунка бачимо, що задані коефіцієнти розкладанняс_пописують коливання трикутної форми.

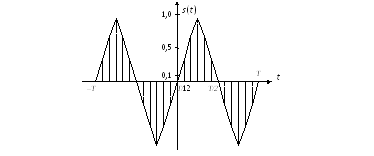
Рисунок 2.13 – Результат розв’язання задачі синтезу

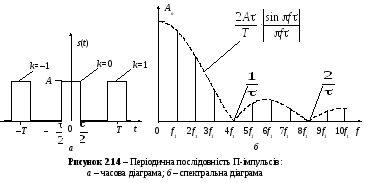
Вправа 2.5.Задано сигнал – періодична послідовність П-імпульсів

Цей сигнал представлено на рис. 2.14, а. Нехай параметри сигналу наступні:А= 1 В,Т= 1 мс, τ = 0,25 мс. Використовуючи доступний пакет математичних розрахунків, обчисліть за виразами (2.39) значення дляА_пдляпвід 0 до 10 та порівняйте отримані результати з теоретичними значеннями

За отриманими значеннями А_ппобудуйте амплітудний спектр сигналу, для прикладу використовуйте рис. 2.14,б.