2.3 Подання сигналів в ортогональних базисах

Серед різноманітних математичних прийомів, які використовуються для опису електричних кіл і сигналів, найбільш широко застосовується подання довільної функції у вигляді суми більш простих (“елементарних”) функцій. Нехай s(t) – детермінований сигнал тривалостіT_s. Представимо його зваженою сумою деяких базисних функцій

, 0tT_s, (2.23)

де a_n–коефіцієнти розкладання;

_n(t) –базисні функції.

Базисні функції вибираються з тих чи інших міркувань, потім розраховуються коефіцієнти розкладання. Але найбільш просто коефіцієнти розкладання розраховуються, якщо базисні функції ортогональні на інтервалі (0, Т_s). Помножимо ліву й праву частини рівності (2.23) на_k(t) і проведемо інтегрування на інтервалі (0,Т_s):

.

Інтеграли в правій частині внаслідок ортогональності функцій _n(t) і_k(t) дорівнюють нулю, крім випадкуn=k, у цьому випадку інтеграл дорівнює енергіїk-ї базисної функції. Тому останню рівність запишемо

.

Повернемося до індексу nі запишемо правило обчислення коефіцієнтів розкладання

;n= 1, 2, 3, ... . (2.24)

Якщо ж базисні функції не тільки ортогональні, а ще й нормовані (ортонормовані), то

n= 1, 2, 3, ... . (2.25)

Ряд (2.23), в якому коефіцієнти розкладання визначаються за формулами (2.24) і (2.25), називається узагальненим рядом Фур'є.

Періодичний сигнал s(t) з періодомТтакож можна подати узагальненим рядом Фур'є. Базисні функції повинні мати періодТабо період у ціле число разів менший заТ; інтервал інтегрування у співвідношеннях (2.24) і (2.25) повинен бути (0,Т); енергії базисних функційЕ_nповинні визначатись на інтервалі (0,Т).

При практичному використанні розкладання (2.23) доводиться обмежуватися скінченним числом доданків, що дає наближений сигнал

. (2.26)

При цьому енергія різниці між s(t) і(похибки) визначається

. (2.27)

Звичайно вважають, що число Nобране так, щоб задовольнити заданій мірі точності, а саме, енергія похибки не перевищує деяке допустиме значення. Тоді в записі розкладання сигналуs(t) використовують знак точної рівності

. (2.28)

Залежно від властивостей сигналу s(t) або задачі, що вирішується, використовують ті чи інші системи базисних ортогональних функцій: тригонометричні функції, експонентні функції, функції відліків, функції Уолша.

Після того, як виконано розкладання сигналу s(t) у ряд, коефіцієнти розкладання повністю задають сигналs(t), тобто за коефіцієнтами можна відновити сигнал. Коефіцієнти розкладання дозволяють також визначити енергетичні характеристики сигналів: енергію сигналуs(t)

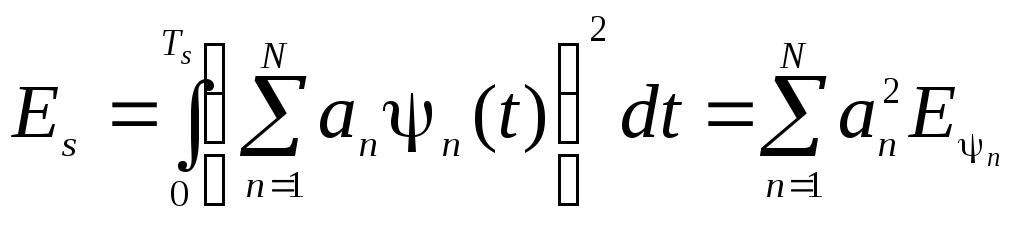(2.29)

і скалярний добуток сигналів s₁(t) іs₂(t)

, (2.30)

де a_n1іa_n2– коефіцієнти розкладання сигналівs₁(t) іs₂(t) відповідно.

Визначення коефіцієнтів розкладання можна виконати й апаратно за схемою, наведеною на рис. 2.7, а. Ця процедура називаєтьсяаналізом сигналу. Знайдені коефіцієнти розкладання повністю описують сигнал. Знаючи їх, можнасинтезувати сигнал–відновити його за коефіцієнтами розкладання(рис. 2.7,б). Схеми, наведені на рис. 2.7, знаходять застосування в техніці зв'язку при деяких методах передавання: у передавальному пристрої виконується аналіз сигналу, каналом зв'язку передаються коефіцієнти розкладання, у приймальному пристрої виконується синтез сигналу.