5.7 Дистанційні властивості сигналів цифрової модуляції

Відстань між канальними символами характеризує їх розрізнюваність під час демодуляції.Відстань між i-м та j-м канальними символамивизначається

.

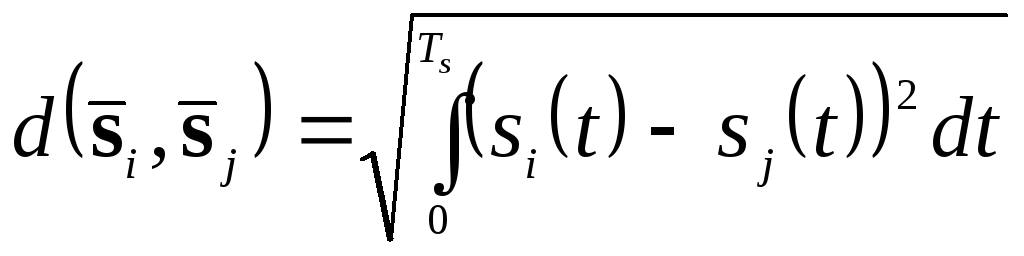Якщо використати аналітичні вирази для канальних символів, то відстань між i-м таj-м канальними символами можна визначити за їх координатами:

– для одновимірних сигналів виразом

,i, j= 0, 1, …,M–1,ij; (5.47)

– для двовимірних сигналів виразом

d(s_i, s_j) =i, j= 0, 1, …,M–1,ij. (5.48)

Для порівняння різних видів модуляції використовують мінімальну відстань

. (5.49)

Відстань d не є фізичним параметром, тому передусім необхідно виразити її через фізичні параметри. Параметром, зручним для порівняння різних видів модуляції, єсередня енергія сигналу, що витрачається на передавання одного біта, Е_б.ЗначенняЕ_бвиражається через фізичні параметри

Е_б=Р_sТ_б =Р_s/R. (5.50)

Порядок визначення мінімальної відстані наступний.

1. Визначаємо візуально на сигнальному сузір’ї мінімальну відстань між канальними символами і позначаємо її d.

2. Виражаємо координати канальних символів на сигнальному сузір’ї через мінімальну відстаньd.

3. Визначаємо енергії канальних символів:

– для одновимірних сигналів

, i = 0, 1, …, M–1; (5.51)

– для двовимірних сигналів

,i = 0, 1, …,M–1. (5.52)

4. Визначаємо середню енергію канального символу

E_сер=. (5.53)

Визначення E_серяк середнє арифметичне випливає з того, що двійкові символи є рівноймовірними, однакову ймовірність 1/Ммають і канальні символи.

5. Визначаємо енергію, що витрачається на передавання одного біту,

Е_б=Е_сер/n, (5.54)

де n– число біт, що передається одним канальним символом.

6. Оскільки після проведення перерахованих дій отримаємо значення Е_б, виражене черезd, то на цьому кроці необхідно виразитиdчерезЕ_бі визначити чисельне значенняd, застосувавши формулу (5.50).

При порівнянні мінімальних відстаней між канальними символами різних методів модуляції слід враховувати, що, чим більша відстань, тим вища ймовірність правильної демодуляції канальних символів.

При порівнянні ширини спектрів сигналів різних методів модуляції слід враховувати, що, чим ширший спектр, тим більший вимагається необхідний частотний ресурс каналу зв'язку для передавання сигналу.

Приклад 5.4.Для сигналів ФМ-4 та ФМ-8 визначимо і порівняємо мінімальні відстань.

З сигнальних сузір’їв (рис. 5.20, а, в) видно, що мінімальна відстань між канальними символами – це відстань від довільної точки сигнального сузір’я до найближчих точок.

З сигнального сузір'я ФМ-4 видно, що d= 2а. Тепер виразимо координати усіх точок через величинуdта результат занесемо до табл. 5.2. Також до цієї таблиці заносимо значення енергії канальних символів розраховані відповідно до виразу (5.52).

Таблиця 5.2 – Координати канальних символів сигналу ФМ-4						Таблиця 5.3 – Координати канальних символів сигналу ФМ-8
si	Кодова комбінація	aci	asi	Еi		si	Кодова комбінація	aci	asi	Еi
s1 s0 s2 s3	01 00 10 11	0,5d – 0,5d – 0,5d 0,5d	0,5d 0,5d – 0,5d – 0,5d	0,5d 2 0,5d 2 0,5d 2 0,5d 2		s1 s0 s2 s3 s7 s6 s4 s5	001 000 010 011 111 110 100 101	1,31d 0,93d 0 – 0,93d – 1,31d – 0,93d 0 0,93d	0 0,93d 1,31d 0,93d 0 – 0,93d – 1,31d –0,93d	1,71d2 1,71d2 1,71d2 1,71d2 1,71d2 1,71d2 1,71d2 1,71d2

У випадку сигналу ФМ-8 через величину d варто спочатку виразити радіус кола r, на якому лежать точки сигнального сузір'я. Для цього розглянемо рівнобедрений трикутник, який утворюється початком координат на сигнальному сузір’ї та канальними символами з початковою фазою135° та180°. Основа цього трикутника дорівнюєd, дві інші сторониr. Висота рівнобічного трикутника ділить його основу навпіл, таким чином маємо два прямокутних трикутника. Кут, що знаходиться біля початку координат дорівнює 22,5°. Відповідно до визначення функції синус можемо записати sin(22,5°) = (d/2)/r, виразимо звідсиr=d/(2sin(22,5°)) = 1,31d. Тепер легко знайти координати канальних символів (табл. 5.3), як координати точок, що лежать на колі

a_ci=rcos(φ_i),a_si=rsin(φ_i), (5.55)

де φ_i– початкова фазаі-го канального символу.

Очевидно, що середня енергія в обох випадках дорівнює енергії довільного канального символу: при ФМ-4 E_сер= 0,5d ², при ФМ-8E_сер= 1,71d ². Пояснюється це тим, що координати канальних символів рівновіддалені від початку координат.

Тепер за виразом (5.54) визначимо енергію, що витрачається на передавання одного біту:

при ФМ-4

Е_б= 0,5d ²/2 = 0,25d ²,

при ФМ-8

Е_б= 1,71d ²/3 = 0,57d ².

І в кінці виражаємо dчерезЕ_б

при ФМ-4

d= 2,

при ФМ-8

d= 1,33.

Порівнюючи отримані мінімальні відстані бачимо, що вони відрізняються у 1,5 раза.

Приклад 5.5.Визначимо у скільки разів відрізняються значення ширини спектра сигналів ФМ-4 та ФМ-8.

Відповідно до виразу (5.28) при фіксованій швидкості цифрового сигналу ширина спектра сигналів різних видів цифрової модуляції відрізняється лише множником у знаменнику log₂M. Таким чином, ширина спектра сигналу ФМ-8 менша ширини спектра сигналу ФМ-4 у

раза.

Отже, за рахунок збільшення числа рівнів модульованого сигналу (кількості канальних символів) зменшується ширина його спектра, однак зменшується і відстань між канальними символами, тобто погіршується їх розрізнюваність під час демодуляції, що проявляється збільшенням ймовірності помилок у демодульованому сигналі.

Вправа 5.10.Задано двійкові сигнали АМ-2, ФМ-2 та ЧМ-2. Побудуйте сигнальні сузір’я заданих сигналів. Визначте величину відстані, виражену через середню енергію модульованого сигналу, що витрачається на передавання одного біта. Порівняйте отримані результати. Порівняйте у скільки разів відрізняються значення ширини спектра заданих сигналів.

Вправа 5.11.Виконати завдання вправи 5.8 для сигналів ФМ-16 та КАМ‑16.