5.2 Спектральна густина потужності сигналу цифрової модуляції

Сигнали цифрової модуляції описуються співвідношенням (5.1). Нехай канальні символи описуються формулою (5.2), в якій – низькочастотний імпульс-переносник. Будемо вважати, що канальні символи, що передаються на різних тактових інтервалахі,, незалежні й рівноймовірні, через те, щоу реальному первинному ЦС двійкові символи 0 і 1 незалежні й рівноймовірні. Внаслідок цієї властивості первинного ЦС коефіцієнтиa_i,a_ci,a_si, що входять у співвідношення (5.2)…(5.4), є випадковими дискретними величинами, рівномірно розподіленими на певному інтервалі, а їх середні значення дорівнюють нулю (це стане очевидним далі).

Для визначення спектральної густини потужності сигналу цифрової модуляції спочатку знайдемо кореляційну функцію сигналу , який описується формулою (5.1):

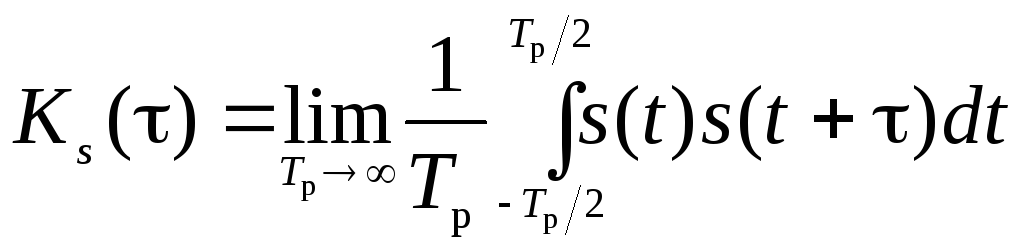, (5.5)

де – тривалість реалізації сигналу.

Нехай , тоді на підставі співвідношень (5.1), (5.2) і (5.5) запишемо

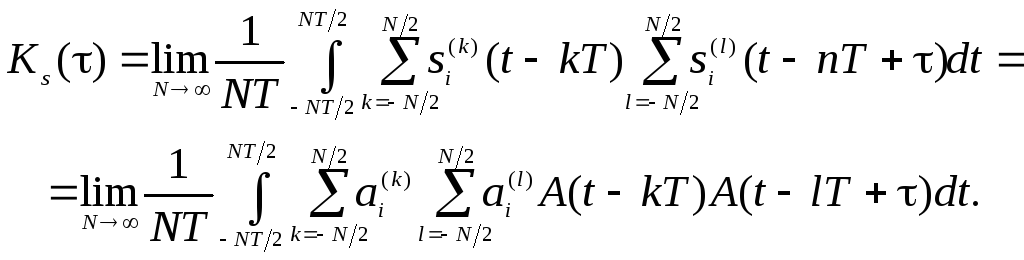(5.6)

Розглянемо добуток сум у співвідношенні (5.6), він дає доданків. Виділимододанків, в яких. Ці доданки дають величину. Для інших доданків у співвідношенні (5.6), для яких, добутки співмножниківйз однаковими ймовірностями набувають певних додатних і від’ємних значень. Ці доданки під час усереднення за часом (за індексомk) дадуть нульовий внесок. На основі викладеного співвідношення (5.6) перепишеться

. (5.7)

Враховуючи, що за визначенням кореляційна функція детермінованого сигналу записується як

, (5.8)

то співвідношення (5.7) перепишеться

. (5.9)

Перейдемо до розгляду сигналів, побудованих на основі канальних символів (5.3). Їх відрізняє від розглянутих НЧ канальних символів те, що використовуються радіоімпульси. За аналогією з викладками, наведеним у прикладах 2.2 і 2.3, неважко отримати вираз для кореляційної функції модульованого сигналу, побудованого на основі канальних символів (5.3):

. (5.10)

У випадку сигналів, побудованих на основі канальних символів (5.4), для отримання виразу для кореляційної функції слід вираз для канальних символів переписати у вигляді радіоімпульсів

, (5.11)

де ,.

Оскільки кореляційна функція радіоімпульсу не залежить від початкової фази, то остаточний вираз для кореляційної функції модульованого сигналу, побудованого на основі канальних символів (5.4), аналогічний виразу (5.10):

. (5.12)

Знайдемо спектральну густину потужності (СГП)модульованихсигналів, використовуючи перетворення Фур’є.Перетворення Фур’є від функціїдає спектр енергії імпульсу, тобто квадрат його амплітудного спектра. Тому для сигналів, побудованих на основі канальних символів (5.2), СГП запишеться

. (5.13)

Порівнюючи формулу (5.9) з формулами (5.10) і (5.12), видно, що вони відрізняються множником . Із властивостей перетворення Фур’є відомо, що множення функції часу наприводить до зсуву її спектра най. Тому для сигналу, побудованого на основі канальних символів (5.3):

. (5.14)

Аналогічно для сигналу, побудованого на основі канальних символів (5.4):

. (5.15)

Зі співвідношень (5.13) – (5.15) випливає, що спектральна густина потужності модульованого сигналу збігається із квадратом амплітудного спектра поодинокого імпульсу-переносника. Отже,ширина спектра сигналу цифрової модуляції визначається шириною спектра імпульсу-переносника.Цей результат дуже важливий для обґрунтування вибору форми канальних символів.