3.8 Білий шум

Білим шумомназивається випадковий процес, СГП якого є постійною величиною

або, (3.52)

де N₀– потужність процесу у смузі 1 Гц.

Визначенням (3.52) відповідають графічні залежності, наведені на рис. 3.9.

КФ білого шумувизначається як зворотне перетворення Фур'є від (3.52)

. (3.53)

На рис. 3.10наведено графікКФбілого шуму.

З виразу (3.53) та рис. 3.10 видно, що інтервал кореляції прямує до нуля, тобто два значення білого шуму, для якихτ ≠ 0,є незалежними. Очевидно, що білий шум має нескінченну потужність і фізично існувати не може, проте є зручною математичною моделлю, яка часто використовується в теорії і техніці зв’язку.

3.9 Перетворення випадкових процесів лінійними електричними колами

Нагадаємо, що за визначенням лінійним електричним коломназивається таке, для якого виконується принцип суперпозиції – реакція кола на суму дій дорівнює сумі реакцій на кожну дію окремо.

При дослідженні проходження випадкових процесів через лінійні кола вважається, що відомі статистичні характеристики вхідного випадкового процесуx(t) та передатна функція лінійного колаH(j). Необхідно знайти характеристики вихідного процесуy(t) (рис. 3.10).

СГП процесу на виході лінійного колазв’язана з СГП вхідного процесу через квадрат АЧХ кола

G_Y() =G_x()H ²(). (3.54)

Зокрема, якщо вхідний процес – білий шум, то СГП вихідного процесу повторює квадрат АЧХ лінійного кола.

КФ процесу на виході лінійного колавизначається як перетворення Фур'є від СГП процесу

K_y() =. (3.55)

Приклад 3.7. Нехай для наочностіx(t) – білий шум з однобічною СГПG_x(f) =N₀, 0f<, подається на вхід ідеального ФНЧ з АЧХ

H(f) =(3.56)

де F_зр– частота зрізу ФНЧ. Визначимо СГП, КФ, інтервал кореляції та середню потужність процесуy(t).

СГП процесу y(t):

G_y(f ) =G_x(f )H²(f ) =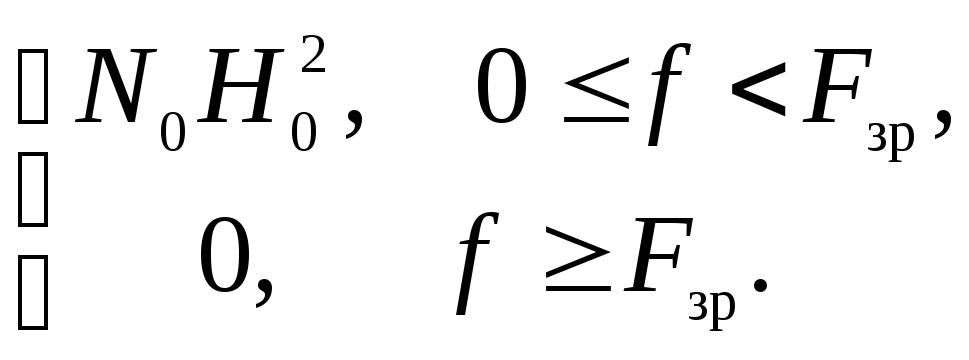(3.57)

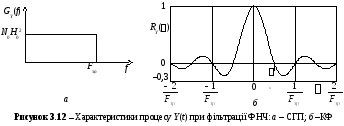
СГП процесу y(t) показано на рис 3.12,а.Шум з СГП такого виду називаютьквазібілим,оскільки вінмає частотні складові однакової амплітуди, але в обмеженому діапазоні частот.

КФ процесу y(t):

. (3.58)

На рис 3,12, бпоказана нормована КФR_Y() =K_Y()/K_Y(0). Інтервал кореляції процесуy(t)_к= 1/(2F_зр).

Середня потужність процесу y(t):

P_y==. (3.59)

В інженерних розрахунках часто виникає задача визначення потужності шуму на виході довільного лінійного кола (неідеального) за умови дії білого шуму з однобічною СГП N₀на його вході¹. Для легкого розв’язання цієї задачі одноразово визначається так званашумова смуга кола, якінтеграл від квадрата нормованої АЧХ кола

F_ш=, (3.60)

де H_max– максимальне значення АЧХ.

За відомої шумової смуги середня потужність P_y обчислюється за виразом

P_y=N₀F_ш. (3.61)

У ідеального ФНЧ шумова смуга фільтра F_ш=F_зр.

Приклад 3.8.Нехайx(t) – білий шум з двобічною СГПG_x(f) =N₀/2, –∞f<, подається на вхід фільтра Баттерворта, нормована АЧХ якого описується виразом

H(f) =, (3.62)

де п– порядок фільтра.

Нехай п= 1. Визначимо КФ процесу на виході фільтраy(t) та його середню потужність:

,

.

Для інтегрування використані такі табличні інтеграли

, .

Для перевірки правильності отриманих результатів можна впевнитись, що виконується властивість КФ K_X(0) =P_X.

Вправа 3.9.Визначте шумову смугу фільтра, заданого у прикладі 3.8, та переконайтесь, що середня потужність, знайдена за її допомогою, буде збігатись з отриманим вище результатом.

Вправа 3.10. Побудуйте графіки КФ і СГП процесу на виході фільтра, заданого в прикладі 3.8, та визначте за ними ширину спектра і інтервал кореляції. Перевірте, чи є добуток τ_кF_maxвеличиною порядку 0,5.

Щодо розподілу ймовірностей процесу, що пройшов через лінійне коло, відомо наступне. Якщо на вході лінійного кола процес гауссів, то вихідний процес також гауссів – вид розподілу не змінюється, змінюються тільки його параметри. Якщо на вході кола процес не гауссів, то вид розподілу змінюється, і вихідний процес має розподіл імовірностей більш близький до гауссового, ніж розподіл вхідного процесу.

Фільтрація є вузькосмуговою,якщо смуга пропускання кола значно менша ширини спектра вхідного процесу. При вузькосмуговій фільтрації має місце явищенормалізації процесу, що полягає в наступному –незалежно від виду розподілу вхідного процесу, розподіл імовірностей процесу на виході кола є гауссовим. Доказ цього явища базується на центральній граничній теоремі теорії ймовірностей.

Приклад 3.9. Чисельним моделюванням доведемо, що розподіл імовірностей миттєвих значень процесу на виході лінійного кола (ФНЧ) тим ближчий до гауссового, чим більшим є відношення ширини спектра процесу на його вході до смуги пропускання кола.

Нехай ФНЧ є фільтром Баттерворта другого порядку, а випадковий процес на його вході – квазібілий шум з рівномірним розподілом в діапазоні значень (0, 2).

Як і у прикладі 3.6, будемо використовувати середовище Matlab. Задамо послідовність незалежних значень вхідного процесу X(t). Тричі розраховуючи параметри фільтра з частотою зрізу 0,5; 0,25 та 0,1 від ширини спектра вхідного процесуF_Хвідповідно, виконаємо фільтрацію тієї самої послідовності значень вхідного процесу. Побудуємо гістограми усіх процесів (рис. 3.13).

Текст М-файла, операції в якому описані вище,наведено в додатку Б.

Вправа 3.11. За аналогією до прикладу 3.9 чисельним моделюванням в середовищі Matlab або іншому, доведіть, що за вузькосмугової фільтрації буде спостерігатися нормалізація випадкового процесу з довільним розподілом миттєвих значень, наприклад, з релеєвським розподілом.

Рисунок 3.13 – Результат вирішення прикладу 3.9