3 Опис випадкових процесів

3.1 Визначення випадкових процесів

У попередніх розділах розглянуті засоби опису детермінованих сигналів. Проте багато задач теорії й техніки зв’язку можуть бути вирішені тільки при описі сигналів і завад випадковими функціями. Випадкова функція якого-небудь аргументу–це така функція, що при кожному значенні аргументу є випадковою величиною. Випадкова функція часу називається випадковим (стохастичним) процесом. Наприклад, напруга завади на виході лінії зв’язку є випадковою функцією часу, тому що ця напруга залежить від безлічі заздалегідь не передбачених і неконтрольованих факторів, які змінюються у часі.

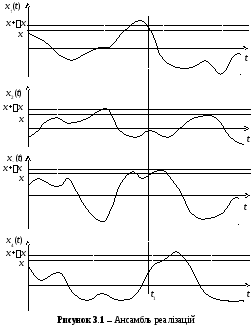
Позначимо випадковий процес, що розглядається, як X(t). Окреміспостереження над процесом, проведені в однакових контрольованих умовах досліду, даютьщораз різні функціїx(t) – різніреалізаціївипадкового процесу.Сукупність{x_k(t)}всіх можливих реалізацій даного випадкового процесу називаєтьсяансамблем(рис. 3.1).Статистичний підхід до опису випадкового процесуполягає в тому, що визначають деякі усереднені характеристики для ансамблю{x_k(t)}у цілому.

3.2 Імовірнісні характеристики випадкових процесів

Найбільш уживаними серед статистичних характеристик випадкових процесів є імовірнісні характеристики. Найпростіша з них – одновимірний розподіл імовірностей. Якщо фіксувати деякий момент часуt₁, то значенняX(t₁) – випадкова величина, різні реалізації набувають різних значень. НехайP{X(t₁)x} –імовірність того, що в моментt₁величинаX(t₁)не перевищує деяке значенняx(рис. 3.1). Тоді

(3.1)

називаєтьсяодновимірною функцією розподілу ймовірностейвипадкового процесуX(t).

Часткова похідна

, (3.2)

якщо вона існує, називаєтьсяодновимірною густиною ймовірностівипадкового процесуX(t)для моментуt₁.

Якщо з тексту ясно, що мова йде про одновимірний розподіл, то індекс 1 у функцій (3.1) і (3.2) опускають. З визначення функції (3.1) випливає, що приx₁<x₂

(3.3)

– різниця значень функції розподілу визначає ймовірність потрапляння значень процесуX(t)у моментt₁в інтервал(x₁,x₂). Застосовуючи (3.3) до визначення функціїp(x,t₁), одержимо

або

(3.4)

– добутокдає наближене значення ймовірності потрапляння значень процесуX(t) умоментt₁вінтервал(x,x+x) (рис. 3.1). Для довільного інтервалу (x₁,x₂)

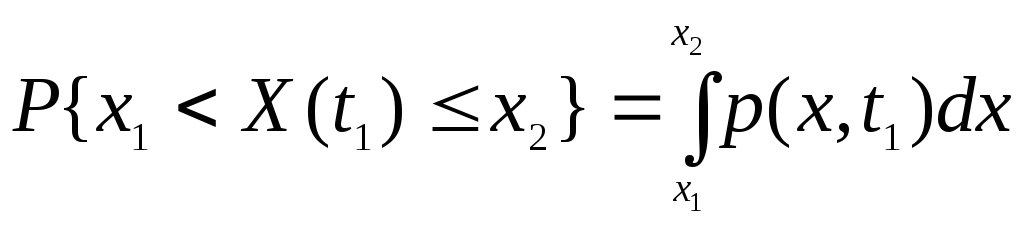. (3.5)

Застосовуючи (3.5) до (3.1), отримаємо, що

. (3.6)

Співвідношення (3.3) і (3.5) виражають одне з основних призначень одновимірних функцій розподілу й густини ймовірності випадкового процесу.

Оскільки сумарна ймовірність усіх можливих значень процесу дорівнює одиниці, то

. (3.7)

Останній вираз називається умовою нормування. Очевидно, щоF(–∞,t₁) = 0, адіапазон можливих значень функції розподілу ймовірностей(0, 1).

Враховуючи, що F(x,t₁) за визначенням є ймовірністю потрапляння в інтервал, розмір якого збільшується зі збільшенням аргументу, вонає не спадною. Останнє обумовлює невід’ємність густини ймовірностіp(x,t₁) ≥0.

Функції F₁(x,t₁) абоp₁(x,t₁) у загальному випадку не можуть бути вичерпними характеристиками випадкового процесу. Адже цей процес, розглянутий у різні моменти часу, являє собою безліч випадкових величин, зв'язаних між собою статистичними залежностями. Зв'язок між двома значеннями випадкового процесуX(t) у моменти часуt₁іt₂ураховується двовимірною функцією розподілу ймовірностей і двовимірною густиною ймовірності.

Двовимірною функцією розподілуймовірностейF₂(x₁,x₂,t₁,t₂)випадкового процесуX(t)називається ймовірність складної події, яка полягає в тому, що в момент t₁ функція X(t)не перевищує деякого значення x₁, а в моментt₂не перевищує значенняx₂

. (3.8)

Двовимірною густиною ймовірностівипадкового процесу X(t) називається часткова похідна другого порядку(якщо вона існує)

. (3.9)

Фіксуючи n= 3, 4, ... моментів часу, за аналогією з (3.7), знаходятьn-вимірну функцію розподілу ймовірностейпроцесуX(t)

. (3.10)

Часткова похідна n-го порядку(якщо вона існує)

(3.11)

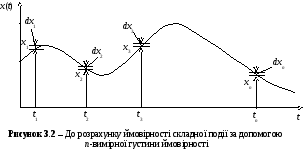
єn-вимірна густина імовірностіпроцесуX(t). Величинавизначає ймовірність складної події, яка полягає в тому, що в моментt₁функціяX(t) перебуває в інтервалі міжx₁іx₁+dx₁, у моментt₂– в інтервалі міжx₂іx₂+dx₂і т.д., зрештою, у моментt_nфункціяX(t) перебуває в інтервалі міжx_nіx_n+dx_n. Інакше кажучи,n-вимірна густина ймовірності, помножена на, визначає ймовірність проходження функціїX(t) черезn“щілин” (рис. 3.2), розміри яких, а ординативідповідно.

Чим більше значення n, тим повніше описано випадковий процес. Але отриманняn-вимірної густини ймовірності абоn-вимірної функції розподілу вимагає надзвичайно складного й трудомісткого оброблення безлічі реалізаційx_k(t) процесуX(t), причому, чим більшеn, тим більш складним і трудомістким є оброблення. Відзначимо, що для рішення багатьох задач достатньо знати одновимірний або двовимірний розподіл імовірностей, оскільки доводиться мати справу з так званимистаціонарнимипроцесами.

Випадковий процес називаєтьсястаціонарним(у вузькому сенсі),якщо для будь-якого цілого числаn1і довільної послідовностісправедлива рівність

, (3.12)

де t₀– будь-яке значення. Інакше кажучи, розподіл імовірностей не залежить від початку відліку часу. Таким чином,статистичні характеристики стаціонарного процесу залишаються незмінними в часі.

З рівності (3.12) випливає, що

(3.13)

– одновимірна густина ймовірності стаціонарного випадкового процесу не залежить від часу.

Для двовимірної густини ймовірності рівність (3.11) набуває виду

.

Вважаючи, що t₀=t₁, одержимо

, (3.14)

де =t₂t₁. З (3.14) випливає, щоу стаціонарних процесів двовимірний розподіл імовірностей залежить не від самих моментівt₁іt₂,а від їхньої різниці.

Далі будемо вважати, якщо не вказано іншого, то випадковий процес є стаціонарним.

Приклад 3.1. Задано одновимірну густину ймовірності стаціонарного процесуX(t)

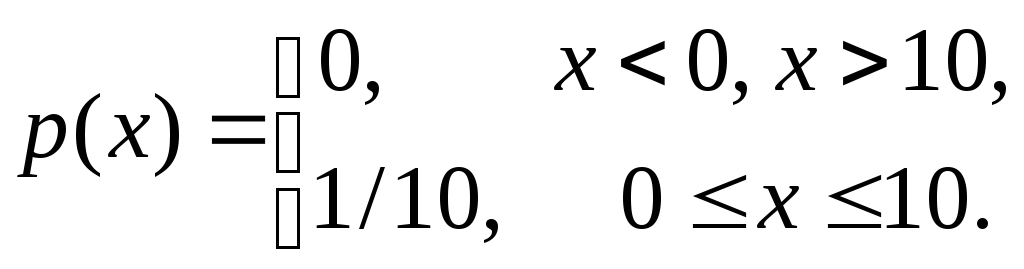
Перевіримо, чи виконується умова нормування заданої густини ймовірності р(х); запишемо функцію розподілу ймовірностейF(x) процесуX(t); за виразомF(x) знайдемо ймовірність потрапляння значень процесуX(t) в інтервал (8, 9).

Використовуючи вираз (3.7) знаходимо

– умова нормування виконується.

Вираз F(x) знаходимо за формулою (3.6), при цьому враховуємо, що в інтервалі –∞ <x< 0 інтегрування дає нуль, а для значеньх> 10 інтегрування дає одиницю

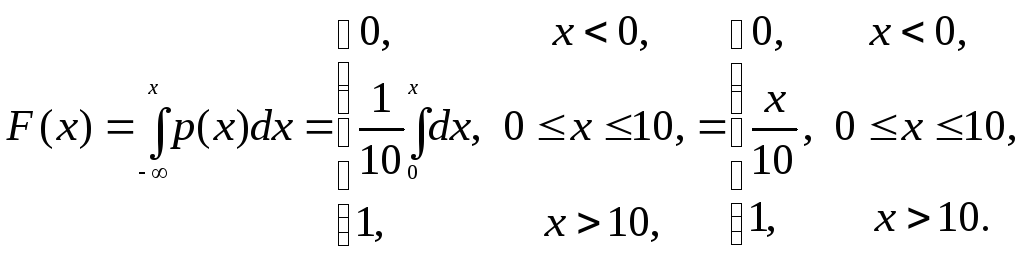
В загальному випадку густина ймовірності рівномірного розподілу описується виразом

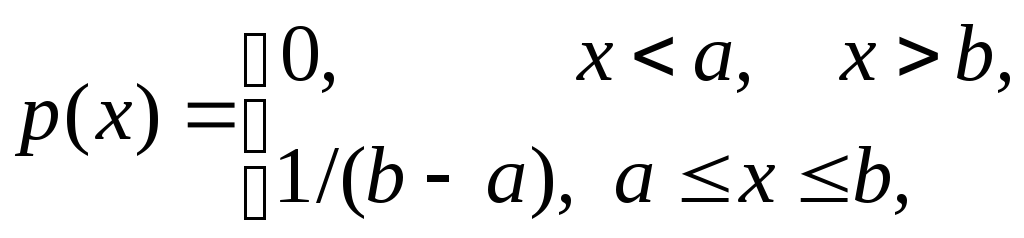(3.15)

а відповідна їх функція розподілу ймовірностей є наступною

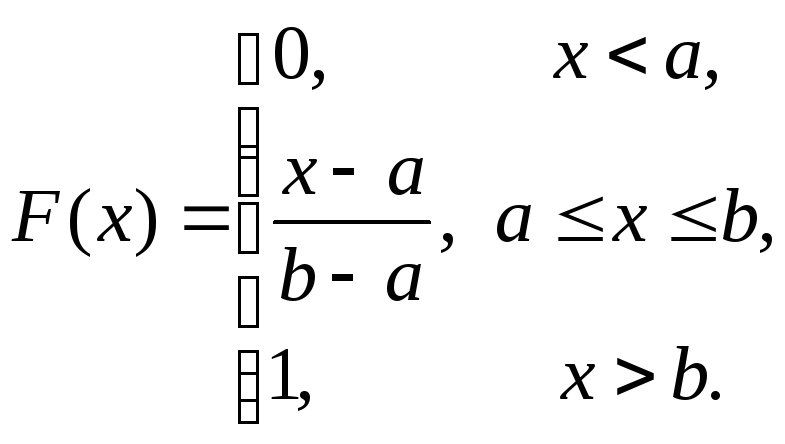(3.16)

Тепер за формулою (3.5) знаходимо

.

Вправа 3.1.Доведіть вираз (3.16) та за його допомогою визначте ймовірність потрапляння значень процесуX(t) в той самий інтервал (8, 9).

Вправа 3.2.Перевірте виконання властивостей функційF(x) ір(х), розглянутих у п. 3.2, для виразів (3.15) і (3.16).