1.3. Поняття загального, часного й базисного рішень

.

Нехай система (І.І) представлена в жордановій формі (1.2). Виразимо базисні змінні через вільні.

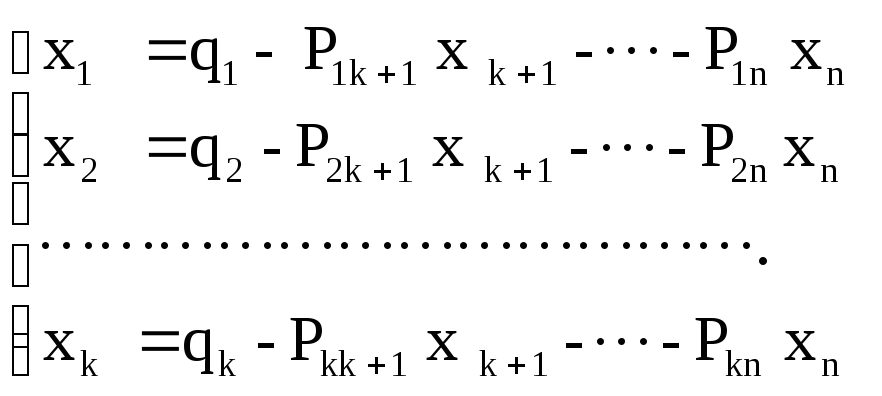(1.6)

(1.6) називається загальним рішенням системи (I.I).

Якщо вільним змінним додати будь-які числові значення й обчислити значення базисних змінних із системи (1.6), то вийде рішення вихідної системи, яке має назву часне. Часне рішення називається базисним, якщо вільні змінні приймають нульові значення. Рішення (1.3) є базисним.

У прикладі загальне рішення таке:

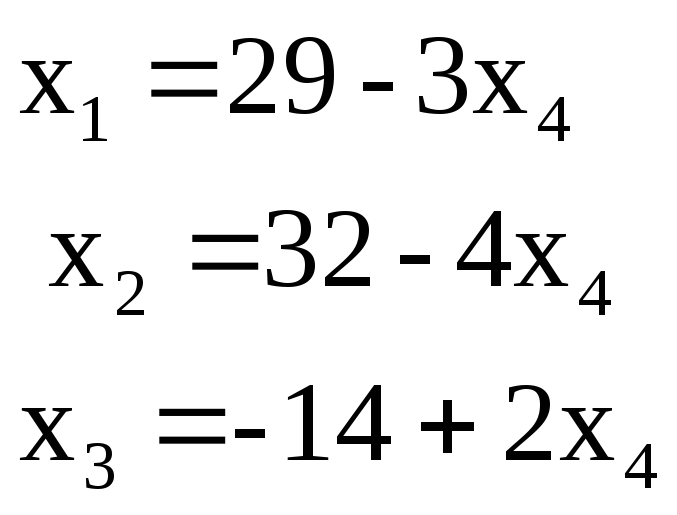
а базисне рішення . Якщо в жордановій формі число рівнянь дорівнює числу змінних n, тобто жорданова форма має вигляд:

то система має єдине рішення; воно є й загальним, і часним , і базисним. Якщо ж k‹n , тобто жорданова форма містить вільні змінні, то система має нескінченно багато рішень.

2. Рішення систем лінійних нерівностей

Лінійною нерівністю називається співвідношення одного з наступних трьох типів:

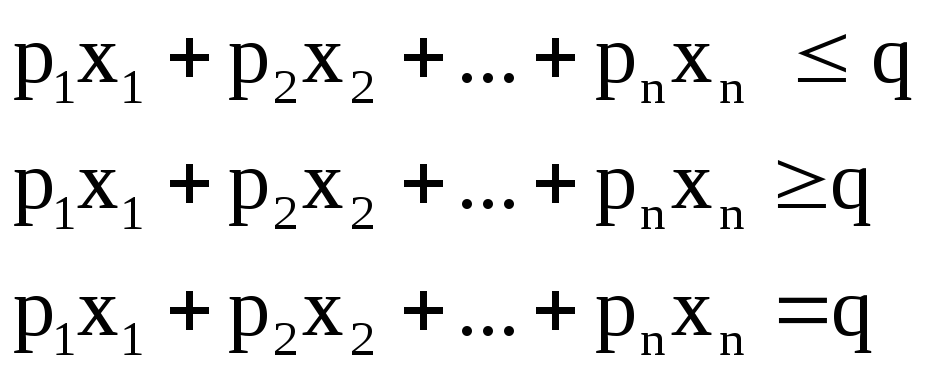
де - дійсні числа.

Наприклад, співвідношення 2х - ≤ 1 або ≥ 0 є лінійними, а співвідношення ≥ 3 або sin x₁ ≤ не є лінійними.

У випадку, коли число змінних у системі дорівнює двом, завдання можна вирішити геометрично. Розглянемо приклади.

Приклад 1

Розглянемо першу лінійну нерівність . Сукупність точок площини, що задовольняють цієї нерівності, являє собою напівплощину, обмежену прямою. Спочатку побудуємо цю граничну пряму (її можна побудувати по двох точках: (0,6) і (9,0). Ця пряма розіб'є площину на дві напівплощини. Щоб вирішити питання про те, яку із цих двох напівплощин визначає нерівність, візьмемо в одній з напівплощин яку-небудь точку, що не лежить на граничній прямій, і підставимо її координати в нерівність. Наприклад, за таку точку візьмемо початок координат - точку (0,0). Оскільки, то напівплощина, обумовлена нерівністю, містить точку (0,0). Аналогічно знаходимо напівплощини, обумовлені іншими обмеженнями. Далі визначимо сукупність рішень заданої системи нерівностей як загальну частину отриманих напівплощин – для заданої системи одержимо опуклий багатокутник.

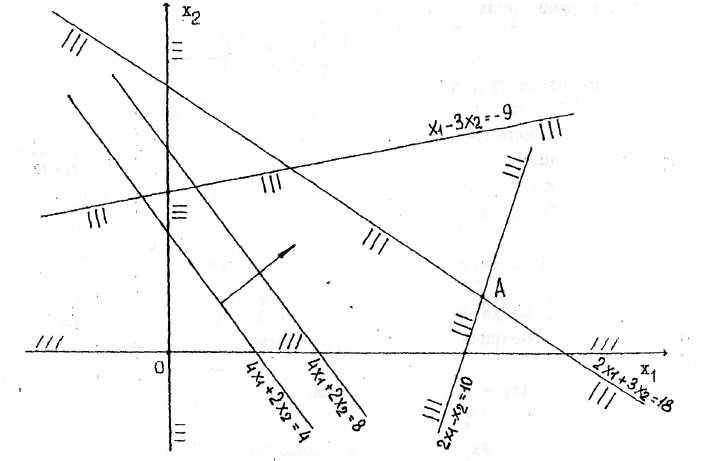
Рис.2.1.

Приклад 2.

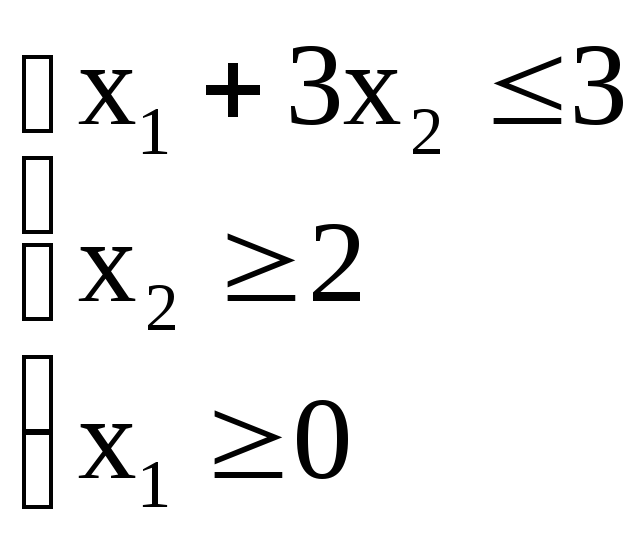
рис. 2.2.

У цьому прикладі напівплощини, обумовлені лінійними нерівностями, не мають загальних точок. Тому задана система нерозв'язна.

3. Рішення нелінійних рівнянь в Excel

Нелінійні рівняння – це рівняння виду f(x)=0, де f(x) – нелінійна функція. Рішення рівняння f(x)=0 зводиться до пошуку таких значень х^* (корінь рівняння), які перетворюють рівняння в тотожність. Розрізняють нелінійні алгебраїчні рівняння й трансцендентні.

Наприклад, нелінійне алгебраїчне рівняння ax² + вx +с =0 має два корені, які можуть бути дійсними або уявними. Наприклад, рівняння х² + 2=0 має два уявних корені х₁= -2 і х₂= --2 .

Надалі буде йтися про обчислення тільки дійсних коренів.

Трансцендентним називається рівняння, якщо в f(x) входить хоча б одна трансцендентна функція. Наприклад, sin(x) -1=0;

Рішення нелінійних рівнянь виконують у два етапи:

1. Етап виокремлення коренів.

2. Етап уточнення коренів, тобто пошук коренів із заданою точністю.

Етап виокремлення коренів

Для цього побудуємо графік заданої функції f(x)=0. У стовпці А розташовуємо зміни аргумента, а в стовпці В табулюємо функцію. Будуємо графік. На графіку виділяємо межі кореня й у цих межах беремо початкове наближення кореня (намалювати графік, виділити корінь і взяти початкове наближення).

Етап уточнення кореня

Команда Підбір параметрів

Порядок уточнення:

1. В комірку A1 вводимо початкове наближення кореня Х₁.

2. В комірку В1 вводимо формулу із заданою функцією.

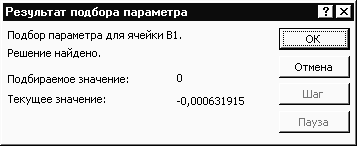
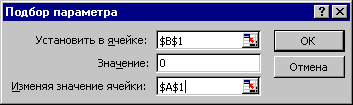
3. Виконуємо команди Сервіс, Підбір параметра. З'являється вікно Підбір параметра (рис. 3.1).

4. В полі "Установити в комірці" записати адресу першої формули (можна зняти вікно й клацнути комірку В1, потім відновити вікно).

5. В полі "Значення" установити 0.

6. В полі "Змінюючи значення комірки" установити адресу А1 (зняти вікно й клацнути А1).

7. Клацнути ОК. З'являється вікно Результат підбору параметра (рис. 3.2), а в комірці А1 буде уточнене значення кореня.

Рис. 3.2

Рис. 3.1